Билет 1
Скалярное произведение
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначаем:
,
.
Поскольку
и
,
то
Свойства
скалярного произведения. Нетрудно
показать, что для произвольных векторов
,
и
,
и для любого числа
справедливо:
;
;
;
,
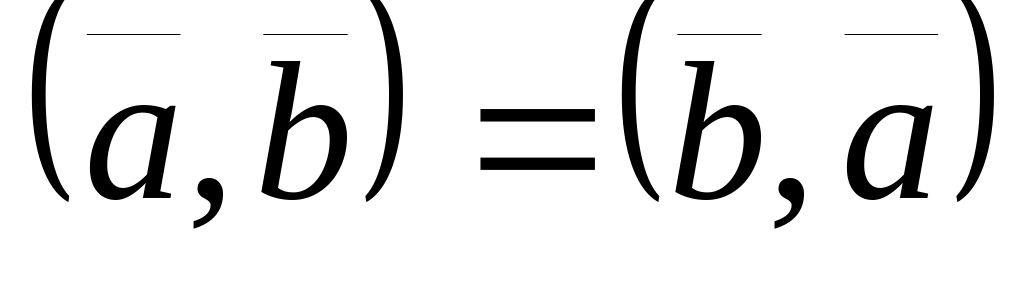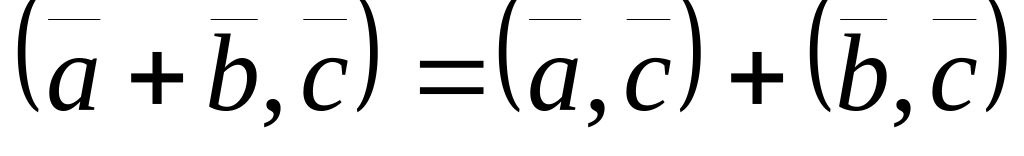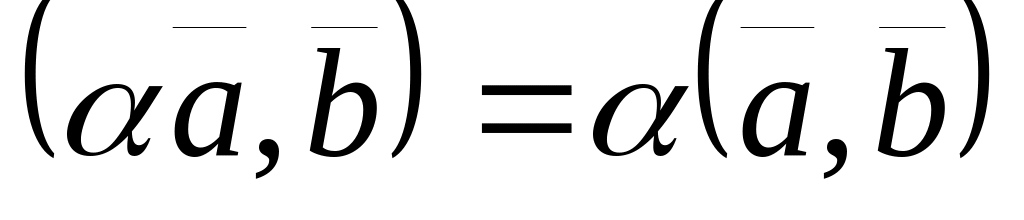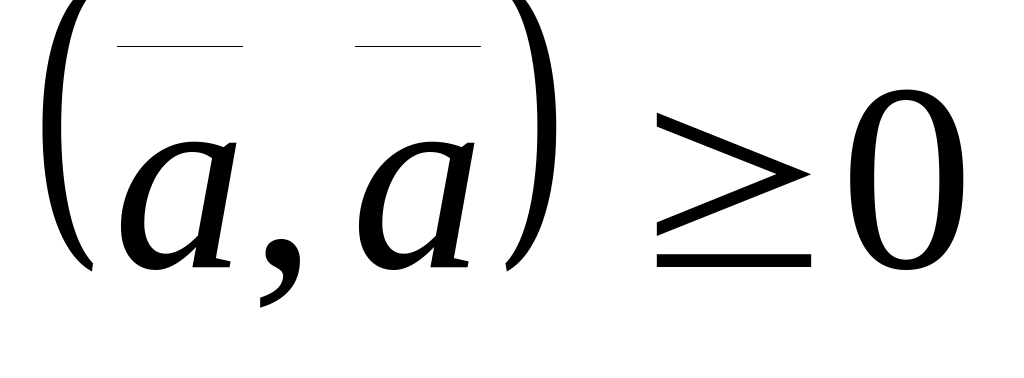причем
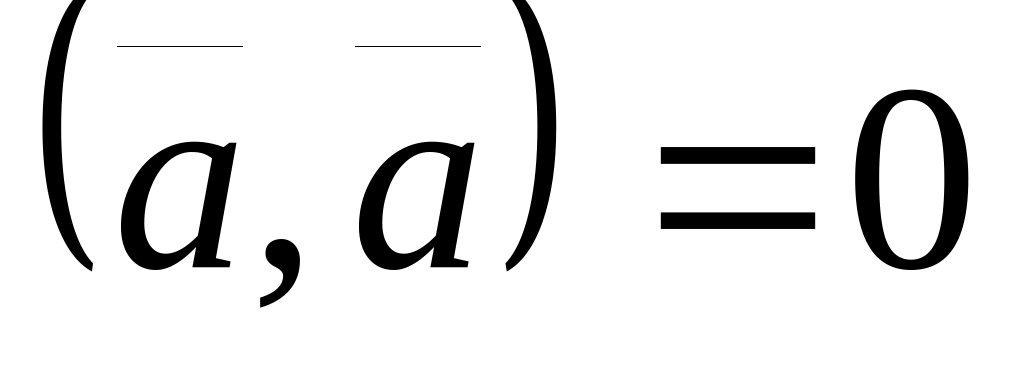тогда и только тогда, когда
.
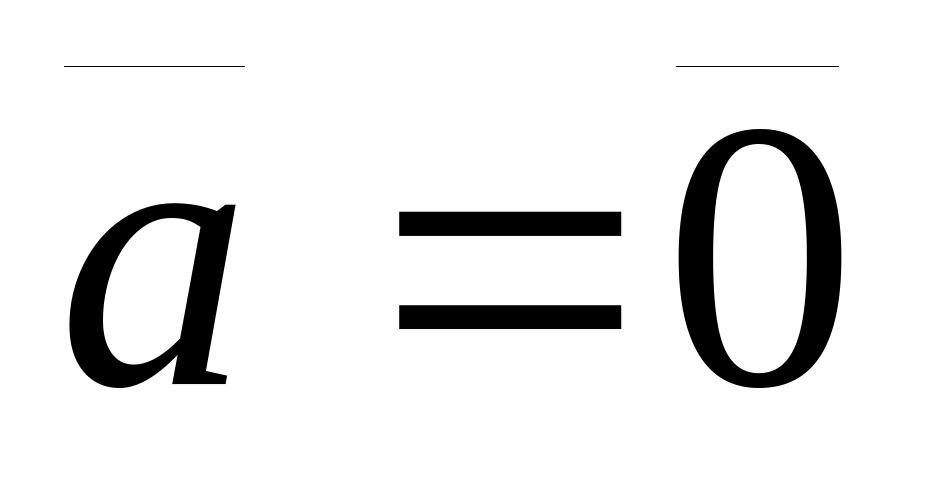Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
;
,
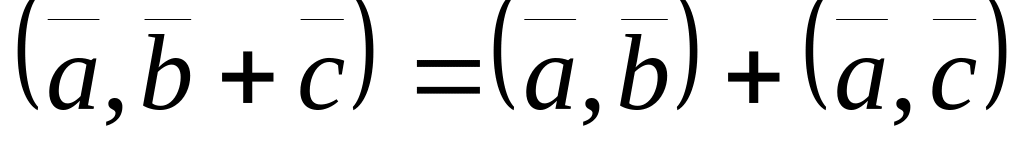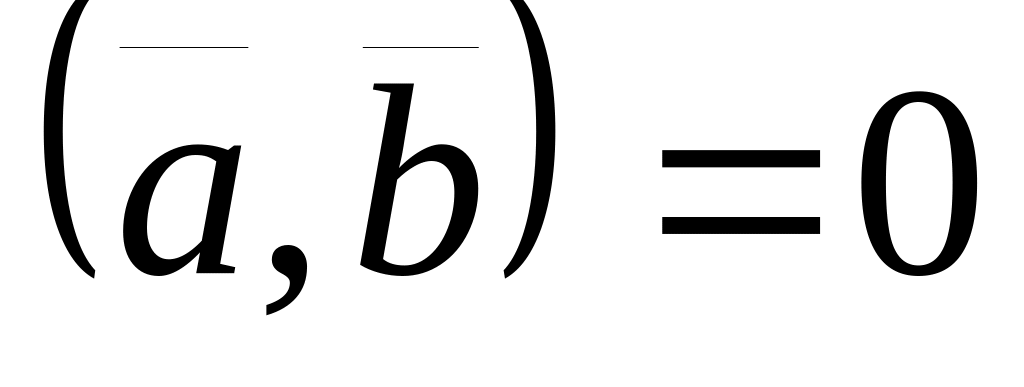тогда и только тогда, когда векторы
и
ортогональны (поскольку направление
нулевого вектора не определено, его
можно считать ортогональным любому
вектору);
;
выражение
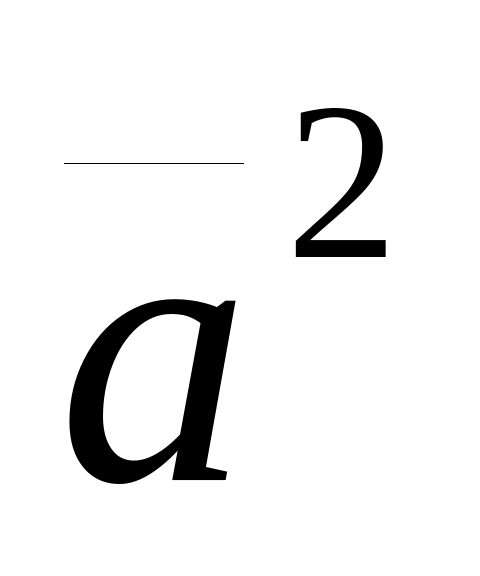называют скалярным квадратом
вектора;если для любого вектора , то вектор — нулевой, т.е. из
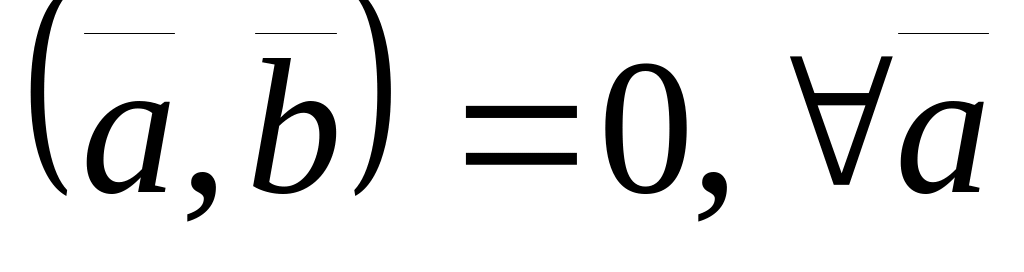следует
;если — угол между векторами и , то
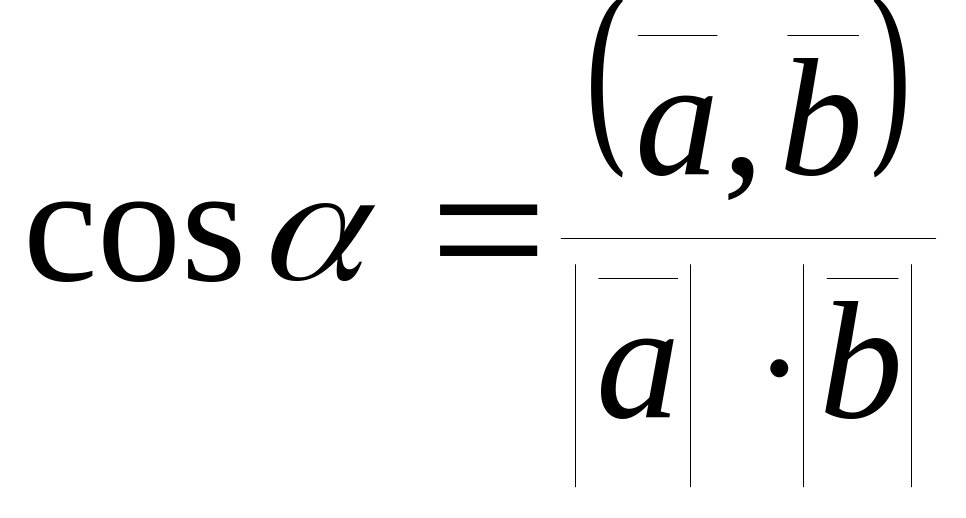;если векторы и заданы своими координатами в некоторой декартовой системе координат:
,
,
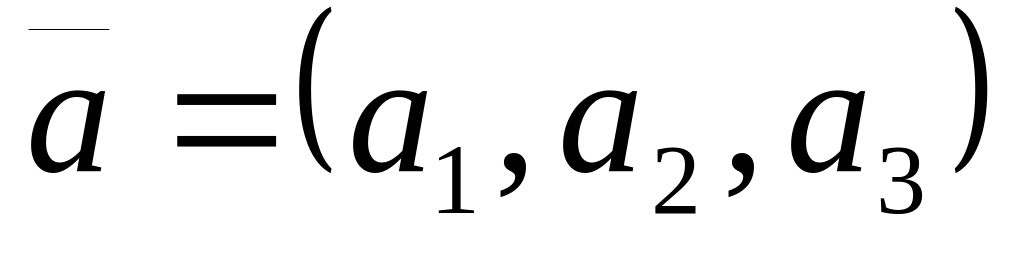то
.
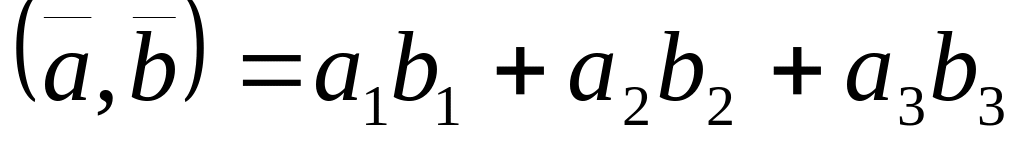Скалярное произведение векторов можно использовать для вычисления углов между векторами: если — угол между векторами и , то .
Равенство нулю скалярного произведения векторов — признак ортогональности векторов: , тогда и только тогда, когда векторы и ортогональны.
Билет 2
Скалярное произведение, вычисления скалярного произведения в координатах.
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначаем: , .
Поскольку и , то
Свойства скалярного произведения. Нетрудно показать, что для произвольных векторов , и , и для любого числа справедливо:
1 ;
2 ;
3 ;
4 , причем тогда и только тогда, когда .
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
1 ;
2 , тогда и только тогда, когда векторы и ортогональны (поскольку направление нулевого вектора не определено, его можно считать ортогональным любому вектору);
3 ; выражение называют скалярным квадратом вектора;
4 Если для любого вектора , то вектор — нулевой, т.Е. Из следует ;
5 если — угол между векторами и , то ;
6 если векторы и заданы своими координатами в некоторой декартовой системе координат: , , то .
Равенство нулю скалярного произведения векторов — признак ортогональности векторов: , тогда и только тогда, когда векторы и ортогональны.
Если векторы
и
заданы своими координатами в некоторой
декартовой системе координат:
,
,
то
,
.
Вычислим
:
,
из свойства 2 и следствия 1 следует:
из свойства 3 и следствия 2 следует:
поскольку
.
Доказано, что .
Билет 3
Векторное произведение
Определение.
Векторным произведением векторов
и
(обозначаем
его
)
называется вектор, который определяется
следующим образом:
,
— угол между векторами
и
;
(определили длину вектора
);вектор ортогонален вектору и вектору ; (определили положение вектора в пространстве);
векторы , и образуют правую тройку; (определили направление вектора ).Правая тройка: из конца вектора поворот от вектора к вектору видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.
Важный пример.
,
,
.
Свойства векторного произведения. Нетрудно показать, что для произвольных векторов , и , и для любого числа справедливо:
;
;
;
.
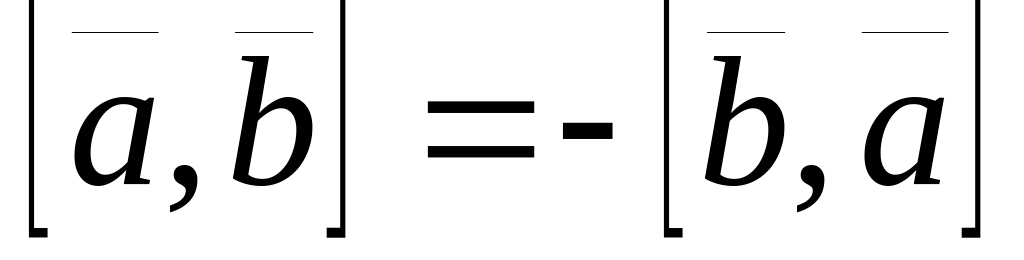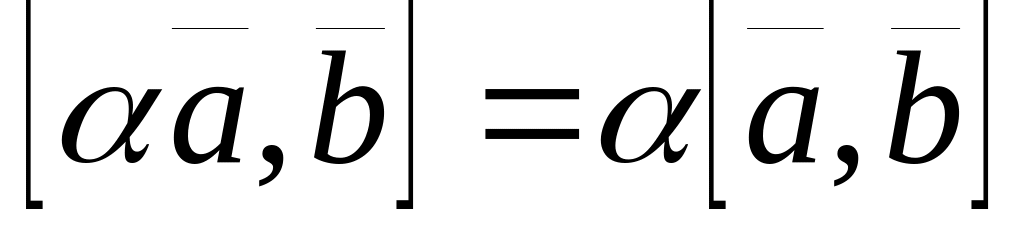Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
;
;
,
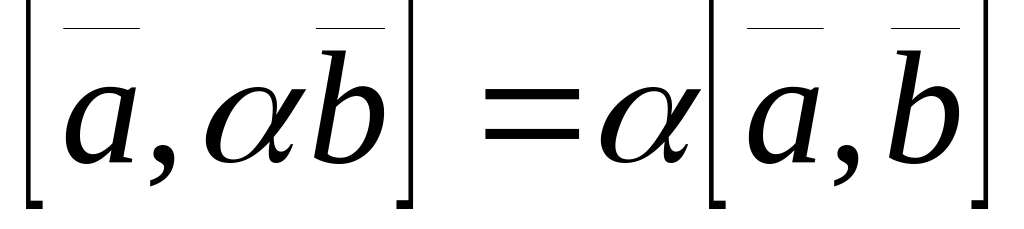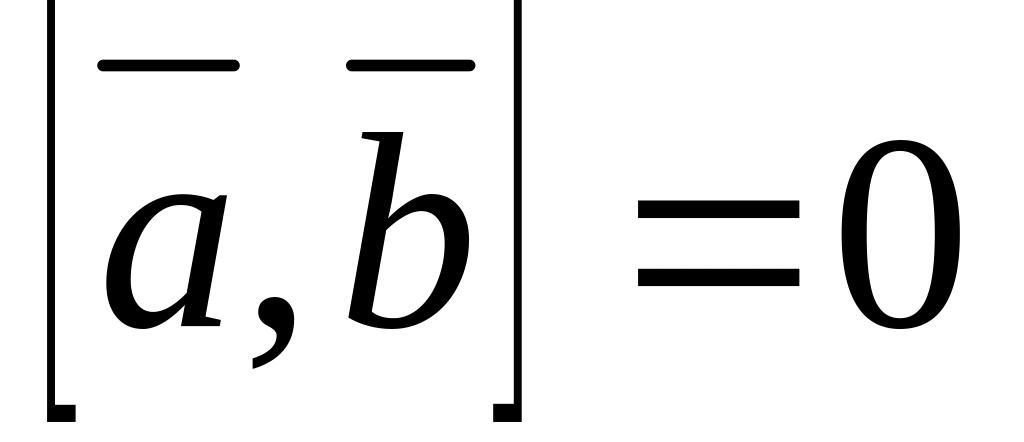тогда и только тогда, когда векторы
и
коллинеарны (лежат на
параллельных прямых); нулевой вектор полагают коллинеарным любому вектору);
длина векторного произведения ( , — угол между неколлинеарными векторами и ) равна площади параллелограмма, построенного на векторах и как на сторонах;
Если векторы и заданы своими координатами в некоторой декартовой системе координат: , , то
Равенство
нулю векторного произведения векторов
— признак коллинеарности векторов:
,
тогда и только тогда, когда векторы
и
коллинеарны
.
.
Билет 4
Векторное произведение, Вычисление векторного произведения в координатах
Определение Векторным произведением векторов и (обозначаем его ) называется вектор, который определяется следующим образом:
, — угол между векторами и ; (определили длину вектора );
вектор ортогонален вектору и вектору ; (определили положение вектора в пространстве);
векторы , и образуют правую тройку; (определили направление вектора ).Правая тройка: из конца вектора поворот от вектора к вектору видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.
Свойства векторного произведения. Нетрудно показать, что для произвольных векторов , и , и для любого числа справедливо:
1) ; 2) ; 3) ; 4) .
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
1) ; 2) ;
3) , тогда и только тогда, когда векторы и коллинеарны (лежат на
параллельных прямых); нулевой вектор полагают коллинеарным любому вектору);
4) длина векторного произведения ( , — угол между неколлинеарными векторами и ) равна площади параллелограмма, построенного на векторах и как на сторонах;