
- •7.Методы измерения статического давления и скорости жидкости
- •8.Течение жидкости называется установившемся, стационарным, если скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).
- •9.Число Рейнольдса
- •13.Последовательное соединение трубок, 2 условия. Вывести формулу для гидравлического соединения последовательно соединенных трубок.
- •1.Закон Ома для переменного тока
- •2. Импеданс - это полное сопротивление в цепи переменного тока, т.Е. Его активная и реактивная составляющие. Обозначают импеданс буквой – z
- •10.Устройство и принцип действия
- •Структура усилителя
- •Каскады усиления
- •Режимы (классы) мощных усилительных каскадов
- •11.Обратная связь в усилителях
- •Амплитудно-частотная характеристика
- •12.Электронные осциллографы предназначены для визуального наблюдения и измерения параметров периодических электрических сигналов.
- •13.Электроды – это проводники специальной формы.Соединяющие измерительную цепь с биологической системой.
- •Резонанс электрических сигналов-
- •3.Рефрактометрия. Подробно объяснить ход опыта по определения показателя преломления прозрачной жидкости рефрактометром. Рефрактометрия
- •10.Характеристики теплового излучения
- •Абсолютно черное тело
- •Типы люминесценции
- •Спектры люминесценции.
- •7.Взаимодействие альфа-частиц с веществом
- •Взаимодействие бета-частиц с веществом
- •8.Взаимодействие рентгеновского и гамма излучения с веществом происходят посредством трех основных процессов: фотоэлектрического поглощения (фотоэффекта), рассеяния и эффекта образования пар.
- •18.3.2. Рассеяние рентгеновского и гамма излучения.
- •Система идентификации
1.

2.

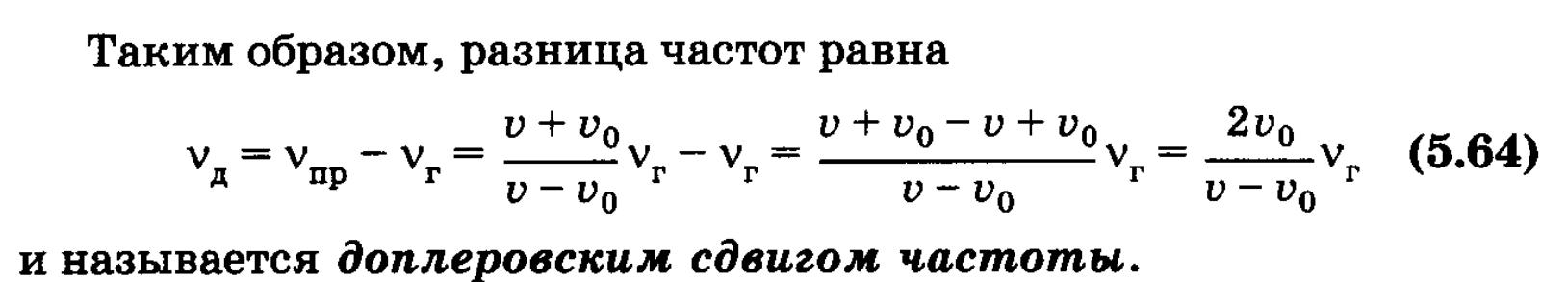
Дифракция звука - отклонение распр.звука от законов геом. акустики , обусловл. его волновой природой. Рез-ты - расхождение зв. пучков при удалении от излучателя.
Интерференция звука - неравномер-ть простран. распределния ампл., результирующий зв. волны в завис-и от соотн. Между фазами волн,с кладыв. В тот или иной точке простр-ва.
3.Звук - колебания с частотой от 16 Гц до 20 кГц, распространяющихся в упругой среде.
Виды звуков: тоны, шумы, звуковые удары.
Волновое сопротивление

4.Объективные характеристики звука-характеристики,не зависящие от св-в приёмника:
1)Интенсивность(сила звука)-энергия,принимаемая зв. Волной за 1 времени через 1 площади,установл. перпенд. вол. звука[Вт/м2];
2)Частота основного тона [Гц];
3)Спектр звука - кол-во обертонов;
5.Ультразвук - механические колебания и волны, частоты кот. От 2*104 до 1010 Гц.
Физические основы применения УЗ в медицине:
 Ко
второму направлению относится
ультрозвуковая физио-терапия.
Ко
второму направлению относится
ультрозвуковая физио-терапия.

6.Идеальная жидкость - жидкость, лишенная вязкости и теплопроводности.
Существует ряд уравнений, описывающих течение идеальной жидкости по трубкам.
1)
Условие
неразрывности струи: при
стационарном течении несжимаемой
жидкости через любые сечения трубки
тока, каждую секунду протекают одинаковые
объемы жидкости, равные произведению
площади сечения (![]() )
на среднюю скорость движения ее частиц
(
)
на среднюю скорость движения ее частиц
(![]() ).
).
![]() -
уравнение неразрывности струи.
-
уравнение неразрывности струи.
Е сли
жидкость движется по системе последовательно
соединенных трубок
различного сечения, то скорость ее
движения обратно пропорциональна
площади сечения трубок (рис. 2.1).
сли
жидкость движется по системе последовательно
соединенных трубок
различного сечения, то скорость ее
движения обратно пропорциональна
площади сечения трубок (рис. 2.1).
сечение 2
сечение 1
Рис. 2.1. Движение жидкости в трубе с разными сечениями (длина стрелок изображает среднюю скорость течения жидкости)
Площадь
сечения пропорциональна квадрату
диаметра
трубки
![]() ,
поэтому
если диаметр трубки в сечении 2 вдвое
меньше,
чем в сечении 1, то площадь поперечного
сечения 2 в четыре раза меньше, чем
площадь сечения 1. Следовательно, и
скорость потока в сечении 2 будет в
четыре
раза
больше, чем в сечении 1.
,
поэтому
если диаметр трубки в сечении 2 вдвое
меньше,
чем в сечении 1, то площадь поперечного
сечения 2 в четыре раза меньше, чем
площадь сечения 1. Следовательно, и
скорость потока в сечении 2 будет в
четыре
раза
больше, чем в сечении 1.
2) Для идеальной жидкости (сила трения полностью отсутствует) справедливо уравнение, которое было получено швейцарским математиком и физиком Даниилом Бернулли (1700 - 1782). Рассмотрим тонкую трубку тока и выделим в ней два произвольных сечения (рис. 2.2).
В
общем случае эти сечения находятся на
различных высотах (h1
и h2),
и их площади различны (S1
и S2).
Вследствие уравнения неразрывности,
различны будут и скорости течения
жидкости в этих сечениях (![]() и
и
![]() ).
Обозначим давления жидкости в этих
сечениях P1
и Р2,
соответственно.
).
Обозначим давления жидкости в этих
сечениях P1
и Р2,
соответственно.

P2
сечение Б
S1
h2
P1
сечение А h1
Рис. 2.2. Параметры сечений в трубке тока
Выделим в трубке тока малый объём жидкости ΔV, массой Δm, который перемещается из положения А в положение Б (рис. 2.2). ΔV = S1·Δl1 = S2·Δl2
Из-за малости объёма ΔV,можно считать, что сечения трубки S1 и S2 на протяжении отрезков Δl1 и Δl2 постоянны.
Перемещение массы Δm жидкости происходит под действием разности внешних сил давления в сечениях А и Б (давление Р2 противодействует движению жидкости).
Сила давления в сечении А: FP1 = P1·S1; в сечении Б: FP2 = P2·S2. FP1> FP2
За
время Δt
частицы жидкости перемещаются в сечении
А
на расстояние
![]() ,
в
сечении Б
на расстояние
,
в
сечении Б
на расстояние
![]()
Работа
силы давления: А = FP1
·Δl1
- FP2·Δl2
=
![]() ,
,
так
как
![]() ,
то A
= P1·
ΔV
- P2·
ΔV
,
то A
= P1·
ΔV
- P2·
ΔV
Эта работа затрачивается на изменение потенциальной и кинетической энергии массы Δm при переходе из положения Б в положение А (из конечного вычитаем начальное).

Перенесём, все компоненты, относящиеся к сечению А, в левую часть уравнения, а компоненты, относящиеся к сечению Б - в правую часть.

разделим всё уравнение на ΔV, получим:

Положения А и Б выбраны произвольно, значит можно утверждать, что в любом месте вдоль трубки сохраняется условие:
 -
это уравнение Бернулли,
-
это уравнение Бернулли,
где
Р - статическое давление, ρgh - гидростатическое
давление, обусловленное движением
жидкости, а
![]() - динамическое давление.
- динамическое давление.
Уравнение Бернулли формулируется так: при стационарном течении идеальной жидкости полное давление, равное сумме статического, динамического и гидростатического давлений, одинаково во всех поперечных сечениях трубки тока.
7.Методы измерения статического давления и скорости жидкости
Установим в разных местах горизонтальной цилиндрической трубы (струи жидкости) одного сечения две трубки: 1) манометрическую трубку, плоскость отверстия которой расположена параллельно движению жидкости; 2) трубку, изогнутую под прямым углом навстречу движению жидкости (трубку Пито)
Манометрическая трубка позволяет измерить статическое давление Рстатич, Трубка Пито (изогнутая) позволяет измерить полное давление Рполное, равное в данном случае сумме статического и динамического давлений. Так как труба горизонтальна, a = 0, то имеем:
 ,
откуда
,
откуда
![]() .
.
Имея систему двух таких трубок, вычисляют скорость потока жидкости.
8.Течение жидкости называется установившемся, стационарным, если скорости частиц в каждой точке потока со временем не изменяются (при этом условии линии тока совпадают с траекториями частиц жидкости).
Вязкость (внутреннее трение) жидкости - свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой.
Движение реальной жидкости при малых скоростях носит слоистый (ламинарный) характер. При установившемся ламинарном течении бесконечно малые слои жидкости скользят относительно друг друга, не перемешиваясь, и сохраняют во времени свои пространственные положения. При возрастании различия в скоростях соприкасающихся слоёв, силы трения между ними также возрастают. Это приводит к тому, что при некоторой критической величине скоростей, разной для разных жидкостей, характер течения существенно меняется. Возникает энергичное перемешивание слоёв жидкости. Положение слоёв в пространстве с течением времени постоянно меняется, появляются вихри. Такое движение называется турбулентным.
Важным свойством турбулентного течения (в сравнении с ламинарным) является высокое сопротивление потоку. Если бы удалось «погасить» турбулентность, то удалось бы достичь огромной экономии мощности двигателей кораблей, подводных лодок, самолетов.
Ньютоновская жидкость:вода.
Неньтоновские жидкости:кровь.
Сила внутреннего трения; закон Ньютона
Предположим, что в ламинарном установившемся потоке жидкости два соприкасающихся слоя имеют скорости V1 u V2 (рис. 1.1).
 x
dV
x
dV
dx
V0 V
Тогда со стороны слоя 1, движущёгося более быстро, на слой 2, движущийся медленнее, действует ускоряющая сила F1. Наоборот, со стороны слоя 2, движущегося медленнее, на более быстрый слой 1 действует задерживающая сила F2. Эти силы внутреннего трения направлены вдоль поверхности соприкосновения слоёв в противоположные стороны и по третьему закону Ньютона их величины одинаковы, то есть F1=F2=Fтр
Величина
силы внутреннего трения Fтр,
возникающая в плоскости соприкосновения
двух скользящих относительно друг друга
слоёв жидкости прямо пропорциональна
площади их соприкосновения S,
величине градиента скорости
![]() и зависит от рода жидкости:
и зависит от рода жидкости:
![]()
где - коэффициент внутреннего трения (вязкость) жидкости.
Уравнение называют законом Ньютона для течения вязкой жидкости. Ньютон получил это уравнение экспериментально. Градиент скорости - показывает изменение скорости слоев жидкости на единице длины и направлен перпендикулярно движению слоев в сторону возрастания скорости движения.
Из уравнения видно, что при возрастании скорости движения слоёв жидкости, при увеличении площади соприкосновения этих слоёв и при увеличении коэффициента вязкости жидкости сила трения возрастает. Следует упомянуть, что на силу трения влияет температура жидкости. При повышении температуры сильно возрастает подвижность молекул, что, в свою очередь, влечёт за собой уменьшение вязкости жидкостей (), поэтому эксперименты следует проводить при стабильной температуре.
