§11. Целевая функция

Целевая функция (ЦФ) может зависеть от внутренних или внешних параметров, а ее максимум соответствует максимальной эффективности разработанной системы ((Х)

или(Y)).

Рекомендации по составлению целевой функции :

1. В ЦФ следует включать как можно меньше параметров, иначе с ней сложно работать и она может потерять физический смысл.

2. В ЦФ включаются ограничения только в виде неравенств и включаются те параметры, от которых она существенно зависит.

3. В ЦФ должны включаться те параметры, изменение которых относительно заданных в ТЗ (техническом задании) представляет интерес для конструктора и возможно.

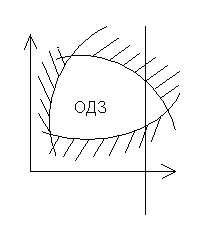^(X,Y) X, Y

Формы целевых функций :

1. ЦФ  зависит от одного внешнего или внутреннего параметра.

^.

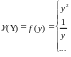Достоинства:

Простота и ясный физико-экономический смысл.

2. ЦФ представляет собой сумму параметров одной размерности или сумму функций от этих параметров.

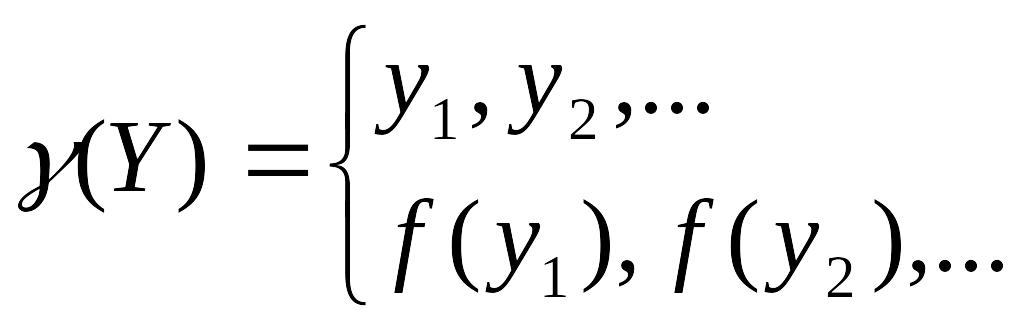
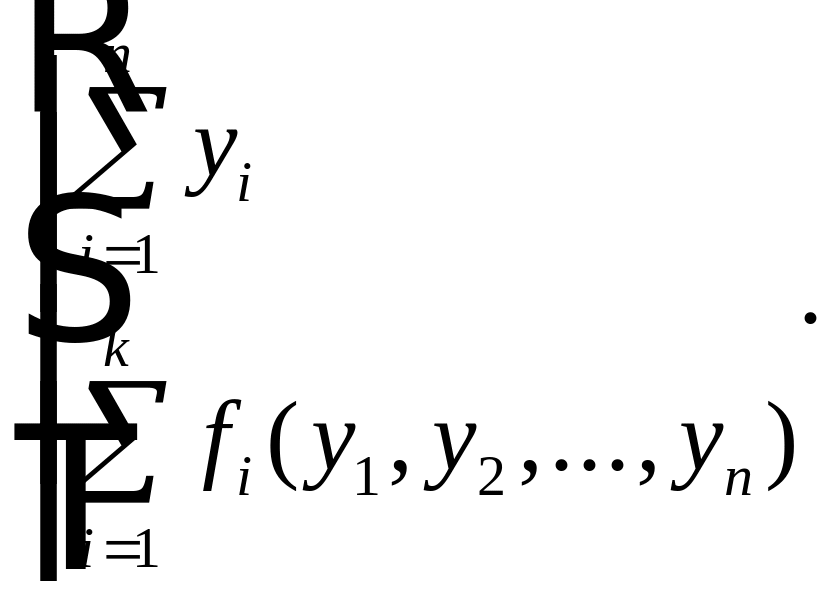
Достоинства:

Простота и ясный физико-экономический смысл,

Позволяет детально описать характеристики системы.

3. Упорядоченная совокупность целевых функций с расставленными приоритетами (ранжированная целевая функция).

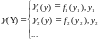
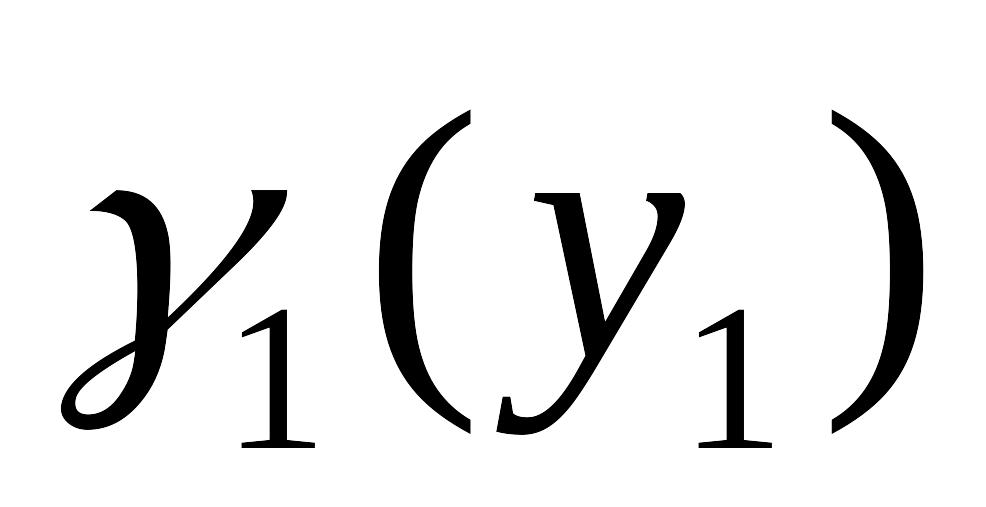
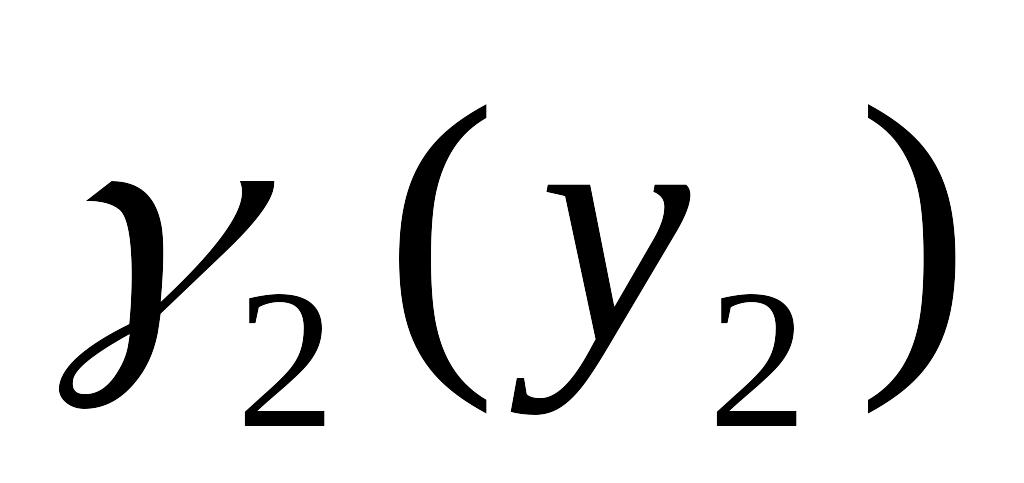
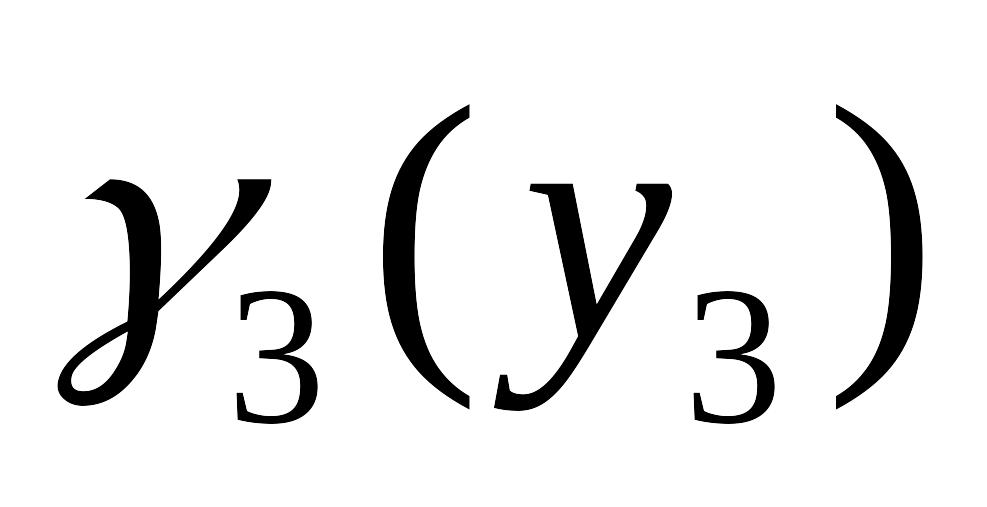
	Вероятность безотказной работы	Стоимость	Масса
I	0,99	100000	18
II	0,99	89000	18
III	0,98	70000	16
IV	0,99	89000	17,5	Оптимальный проект

4. ЦФ произвольной формы и зависит от части, либо от всех внешних параметров.

§12. Методы решения задач оптимального проектирования. Классификация

Методы решения задач оптимизации или отыскания экстремума функции можно разделить на следующие группы:

1. Методы классической математики.

2. Методы математического программирования.

3. Метод регулярного поиска.

4. Экспериментальные методы оптимизации.

Методы классической математики:

1. Поиск экстремума функции одной переменной;

2. Поиск экстремума функции многих переменных;

3. Метод замены переменных;

4. Метод неопределенных множителей Лагранжа;

5. Метод вариационного исчисления и др.

Основа методов: по всем переменным берутся частные производные, приравниваются к нулю, решается система уравнений и т.о. находится внутренний локальный экстремум. Далее находится значение ЦФ в локальном экстремуме, на границах области допустимых значений. Все значения сравниваются, и выбирается лучшее.

Недостатки:

1. ЦФ должна быть дифференцируема;

2. методы предназначены для решения задач без ограничений.

3. трудность решения систем уравнений (после того, как взята производная).

Методы математического программирования:

1. Линейное программирование (ограничения на ЦФ являются линейными функциями):

   • симплексный метод,

   • венгерский метод.

2. Выпуклое программирование (ЦФ обладает свойствами выпуклости);

3. Нелинейное программирование;

4. Геометрическое программирование (ЦФ и ограничения имеют вид положительных полиномов - позиномов);

5. Динамическое программирование (ЦФ в виде суммы функций, каждая из которых зависит от одной переменной);

6. Стохастическое программирование (целевая функция и ограничения являются случайными функциями).

Поисковые методы оптимизации:

1. Метод регулярного поиска (где последующий шаг зависит от результата предыдущего)

   • градиентный метод;

   • наискорейшего спуска;

   • штрафной функции и т.д.

2. Методы случайного поиска:

   • со случайным шагом;

   • со случайным направлением;

   • со случайным шагом и направлением.

Достоинства:

1) не накладывают ограничения на целевую функцию и ограничения.

Экспериментальные методы оптимизации:

Экспериментальным путем находится модель некоторого технологического процесса, а затем модель оптимизируется этими же методами. Для этого составляется матрица планирования, проводятся эксперименты.