Элементы теории графов

Граф можно представить себе как множество точек Х на плоскости , называемых вершинами и, множество направленных отрезков U , соединяющих все или некоторые из этих вершин и называемых ребрами, т.е. граф G можно определить как пару множеств G = ( X , U ) . Граф G можно определить также как пару (Х,Г) , где,Г- отображение Х в Х .

Две вершины графа называются смежными , если они определяют ребро графа .

Каждому ребру g соответствует некоторая пара вершин , будем говорить , что они инцидентны друг другу, и отражать этот факт в виде . Два ребра графа называются смежными, если они имеют концами общую вершину. Вершина, неинцидентная никакому ребру графа, называется изолированной. Если граф состоит из изолированных вершин, его называют ноль - графом.

Ребро графа называется неориентированным, если порядок расположения его концов (направление стрелок в графе) не принимается во внимание. Ребро графа называется ориентированным, если этот порядок существен. В случае ориентированного ребра говорят, что - начальная вершина ребра, а - конечная. Ориентированное ребро иначе называется дугой графа.

Граф называется неориентированным, если каждое его ребро неориентировано, и ориентированным, если ориентированы все его ребра. Смешанным графом называется граф, имеющий как ориентированные, так и не ориентированные ребра. Для каждого графа G(x) существует обратный граф G^-1(x), полученный изменением ориентации каждого из ребер графа G(x) на противоположную.

Полным неориентированным графом называется граф V(x), ребрами которого являются всевозможные пары для двух возможных вершин . Полным ориентированным графом называется граф, у которого любые две вершины соединены хотя бы в одном направлении.

Деревом называют конечный связный неориентированный граф, не имеющий циклов. Такой граф не имеет кратных ребер. Начальная вершина х₀ называется корнем дерева. Ветвями дерева называются ребра графа, входящие в дерево.

Лагранжевым деревом называется дерево, все ветви которого имеют общую вершину.

Лесом называется несвязный граф, каждая компонента связности которого является деревом.

Задача о кратчайшем пути

Задача о кратчайшем пути на графе в общем виде может быть сформулирована следующим образом.

Дан неориентированный граф Каждому ребру этого графа приписано некоторое число , называемое длиной ребра. В частных случаях может быть расстоянием между вершинами, соединяемыми ребром , временем или стоимостью проезда по этому ребру и т.п.

Требуется для произвольных вершин а и в графа найти путь , причем такой, чтобы его полная длина была наименьшей.

Нахождение кратчайшего пути в графе с ребрами единичной длины

Вершины такого графа обычно представляют собой состояния некоторой системы , в которой все переходы , делаемые за один шаг, эквивалентны.

Рассмотрим один из нетривиальных методов решения поставленной задачи , который можно назвать как способ приписывания индексов к вершинам.

Общее правило для нахождения кратчайшего пути на графе состоит в том, чтобы каждой вершине приписать индекс , равный длине кратчайшего пути из данной вершины в конечную. Приписывание индексов вершинам в случае графа с ребрами единичной длины производится следующим образом :

Конечной вершине приписыватся индекс 0 .
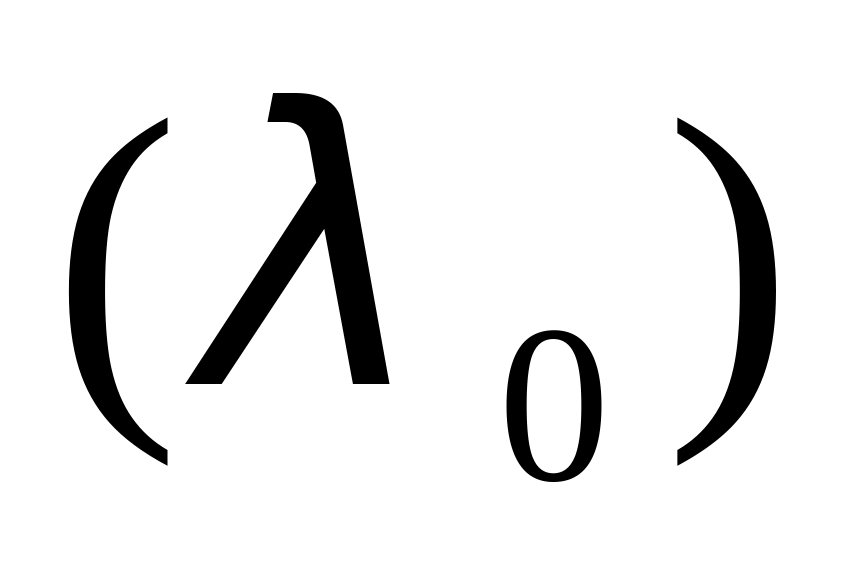Принимаем текущую координату .
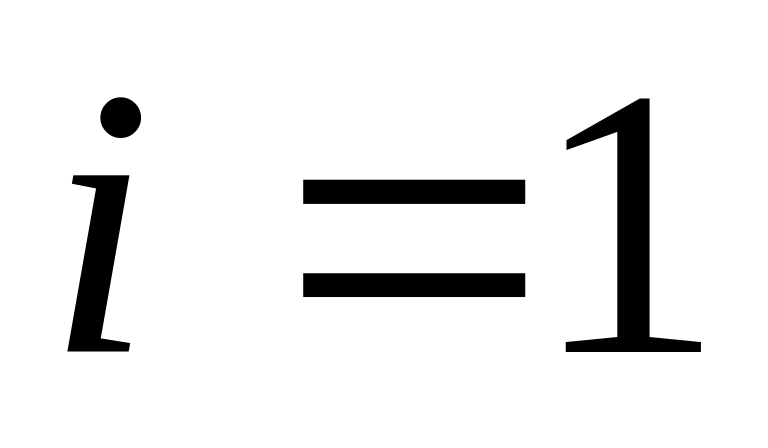Всем вершинам без индекса , из которых идет ребро в вершину , отмеченную 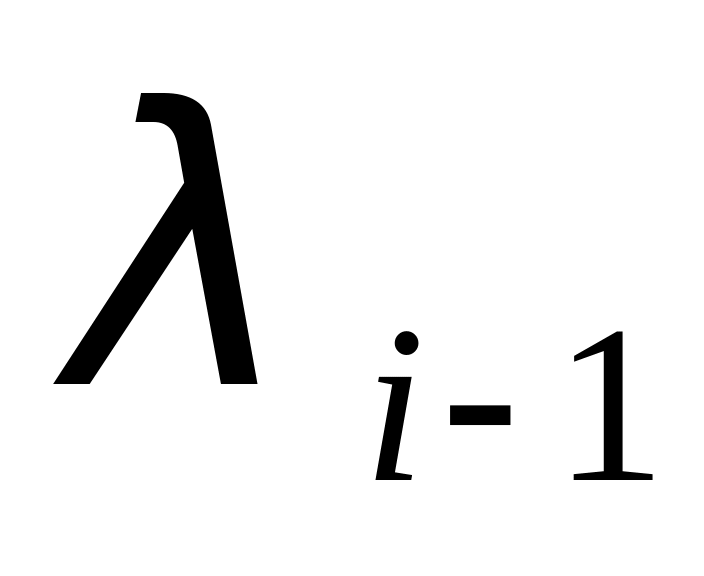, приписывается индекс .
Если начальной вершине еще не приписан индекс , то к текущей координате прибавить единицу 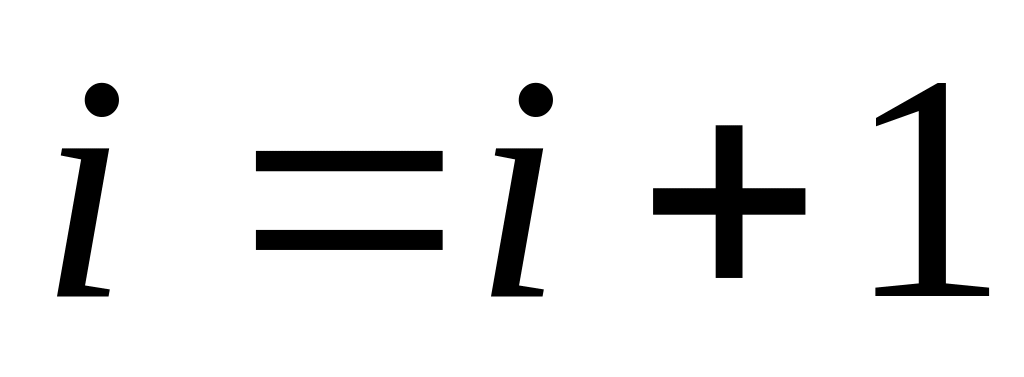и перейти к 3.
Индекс начальной вершины соответствует длине кратчайшего пути. Сам кратчайший путь находится, если двигаться из начальной вершины, в направлении убывания индексов.