
- •Дискретная математика
- •Реализация функций формулами
- •Важнейшие замкнутые классы
- •Этот класс содержит ровно булевых функций , зависящих от переменных .
- •Этот класс также содержит ровно булевых функций , зависящих от переменных и замкнут . Функция называется двойственной для функции .
- •Алгоритмы построения минимальных дизъюнктивных нормальных форм Совершенная дизъюнктивная нормальная форма (д.Н.Ф.)
- •Способы построения тупиковых д.Н.Ф.
- •Критерий поглощения.
- •Локальные алгоритмы упрощения д.Н.Ф.
- •Необходимое и достаточное условие вхождение конъюнкции в
- •Пусть и .
- •Двоичный-симметричный канал
- •Канал , в котором в каждом слове длины n может произойти любая ошибка заданного типа кратности не более s
- •Примеры кодов с исправлением одиночных ошибок различных типов.
- •Очевидно , что число w(X) равно сумме номеров единичных символов слова х.
- •Элементы теории графов
- •Задача о кратчайшем пути
- •Нахождение кратчайшего пути в графе с ребрами единичной длины
- •Нахождение кратчайшего пути на графе с ребрами произвольной длины
- •Задачи, решаемые методами теории потоков
- •Основные понятия и определения теории потоков Конечный граф (х,т) без петель называется сетью , если каждой дуге
- •В любой сети максимальное значение суммарного потока на конечных дугах равно минимальной пропускной способности разреза.
- •Определение максимального потока методом разметки вершин
- •Последовательность решения примера
- •Транспортная задача по критерию стоимости
Важнейшие замкнутые классы
1.
Класс
![]() ,
класс , сохраняющий константу 0 .
,
класс , сохраняющий константу 0 .
Этот класс содержит ровно булевых функций , зависящих от переменных .
2.
Класс
![]()
![]() ,
класс , сохраняющий константу 1.
,
класс , сохраняющий константу 1.
Этот класс также содержит ровно булевых функций , зависящих от переменных и замкнут . Функция называется двойственной для функции .
3.
Класс
![]() -
класс всех самодвойственных функций
, т.е. функций
таких
, что
-
класс всех самодвойственных функций
, т.е. функций
таких
, что
![]() .
Число
самодвойственных функций равно
.
Число
самодвойственных функций равно
![]() .
.
Лемма
1. Если
![]() ,
то из нее путем подстановки функций
и
,
то из нее путем подстановки функций
и
![]() можно получить несамодвойственную
функцию одной переменной, т.е. константу.
можно получить несамодвойственную
функцию одной переменной, т.е. константу.
Класс М – класс всех монотонных функций .
Дадим ряд определений .
Для
двух наборов
![]() и
и
![]() выполнено отношение предшествования
выполнено отношение предшествования
![]() ,
если
,
если
![]() .
.
Два
набора
![]() и
и
![]() называются
сравнимыми , если один из них предшествует
другому .
называются
сравнимыми , если один из них предшествует
другому .
Два
набора
и
![]() называются
соседними , если
называются
соседними , если
![]() ,
,
![]() .
.
Функция
![]() называется
монотонной , если для любых наборов
и
таких
, что
, имеет место неравенство
называется
монотонной , если для любых наборов
и
таких
, что
, имеет место неравенство
![]() .
.
Лемма
2 . Если
![]() ,
то из нее путем подстановки констант
0 и 1 и функции х
можно получить
.
,
то из нее путем подстановки констант
0 и 1 и функции х
можно получить
.
Класс L – класс все линейных функций .
Лемма
3. Если
![]() ,
то из нее путем подстановки констант
0 и 1 и функций
и
,
а также , быть может , путем навешивания
отрицания над
,
можно получить функцию
,
то из нее путем подстановки констант
0 и 1 и функций
и
,
а также , быть может , путем навешивания
отрицания над
,
можно получить функцию
![]() .
.
Теорема о функциональной полноте
Для того чтобы система функций D была полной , необходимо и достаточно , чтобы она целиком не содержалась ни в одном из пяти замкнутых классов
![]()
Теорема . Из всякой полной в системы функций можно выделить полную подсистему , содержащую не более четырех функций .
Теорема Поста. Каждый замкнутый класс из имеет конечный базис .
Алгоритмы построения минимальных дизъюнктивных нормальных форм Совершенная дизъюнктивная нормальная форма (д.Н.Ф.)
Введем
обозначение :
![]() ,
где
,
где
![]() -
параметр , равный 0 либо 1.
-
параметр , равный 0 либо 1.
Очевидно,
что
![]()
Теорема.
Каждую
функцию алгебры логики
![]() при
любом
при
любом
![]() можно
представить в следующей форме :
можно
представить в следующей форме :
![]() ,
(1)
где дизъюнкция берется по всевозможным
наборам значений переменных
,
(1)
где дизъюнкция берется по всевозможным
наборам значений переменных
![]() .
.
Это
представление называется разложением
функции по m
переменным.
Зададим переменным произвольные
значения
![]() и подставим их в правую часть равенства
(1) , получим
и подставим их в правую часть равенства
(1) , получим
![]()
=![]()
![]()
![]()
.
В качестве следствия имеем два специальных случая :
 ;
; .
.
Если функция не равна тождественно нулю, то последнее равенство может быть преобразовано к виду :
![]() .
.
Такое представление функции носит название совершенной д.н.ф. Аналогично введем понятие совершенной конъюктивной нормальной формы . Будем называть совершенной к.н.ф. разложение вида :
![]() .
.
Основные понятия теории д.н.ф.
Элементарной
конъюнкцией называется
логическое произведение
![]() ,
где все переменные различны. Число
,
где все переменные различны. Число
![]() называется рангом конъюнкции .
называется рангом конъюнкции .
Д.н.ф.
называется дизъюнкция
![]() элементарных конъюнкций, в которой все
элементарных конъюнкций, в которой все
![]() различны. Число m
называется
длиной д.н.ф.В случае m
= 0 д.н.ф.
называется пустой и полагается равной
0.
различны. Число m
называется
длиной д.н.ф.В случае m
= 0 д.н.ф.
называется пустой и полагается равной
0.
Минимальной
д.н.ф. функции
![]() называется д.н.ф. , реализующая эту
функцию и содержащая наименьшее число
символов переменных по сравнению со
всеми другими д.н.ф. реализующими
.
называется д.н.ф. , реализующая эту
функцию и содержащая наименьшее число
символов переменных по сравнению со
всеми другими д.н.ф. реализующими
.
Кратчайшей д.н.ф. функции называется д.н.ф., реализующая эту функцию и содержащая наименьшее число элементарных конъюнкций по сравнению со всеми другими д.н.ф. реализующими .
Теорема.
Число
различных д.н.ф. составленных из
переменных
![]() ,
равно
,
равно
![]() .
.
Обозначим
![]() -
множество вершин единичного n-
мерного куба. Каждой функции
поставим в соответствие подмножество
-
множество вершин единичного n-
мерного куба. Каждой функции
поставим в соответствие подмножество
![]() всех таких вершин
всех таких вершин
![]() ,
что
,
что
![]() Такое соответствие является взаимно
однозначым и обладает следующими
свойствами :
Такое соответствие является взаимно
однозначым и обладает следующими
свойствами :
функции
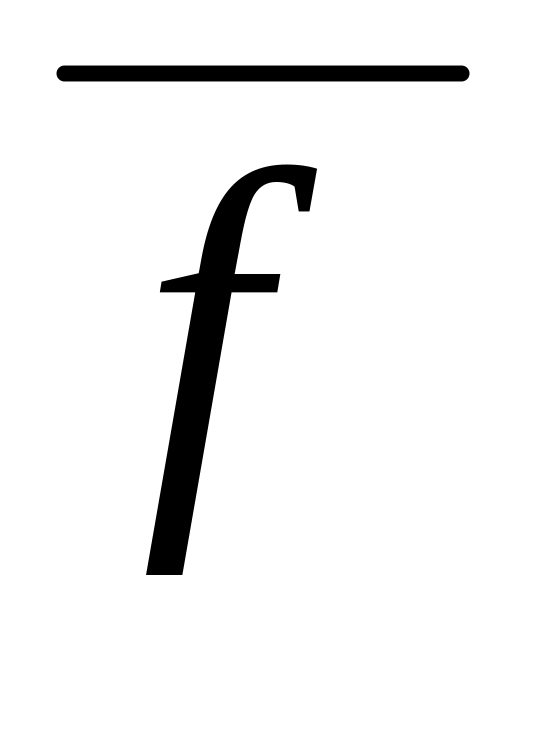 соответствует подмножество
соответствует подмножество
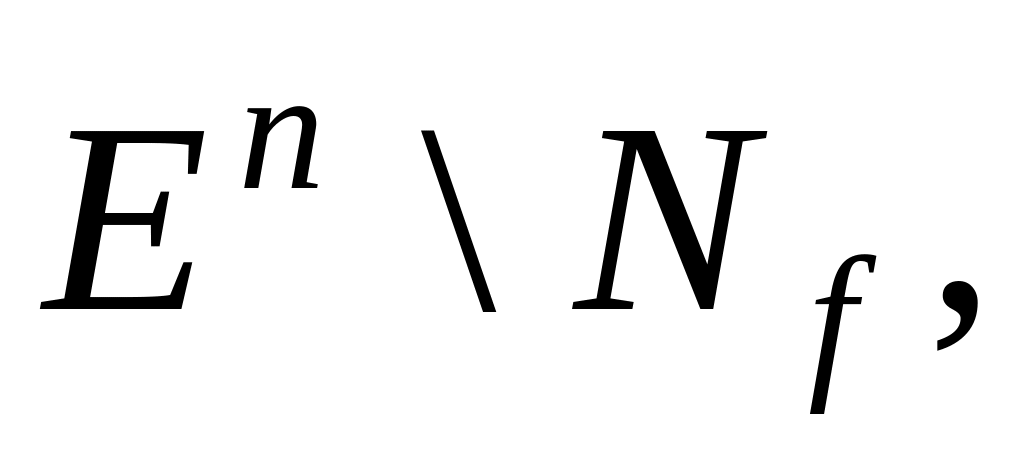
функции
 соответствует подмножество
соответствует подмножество
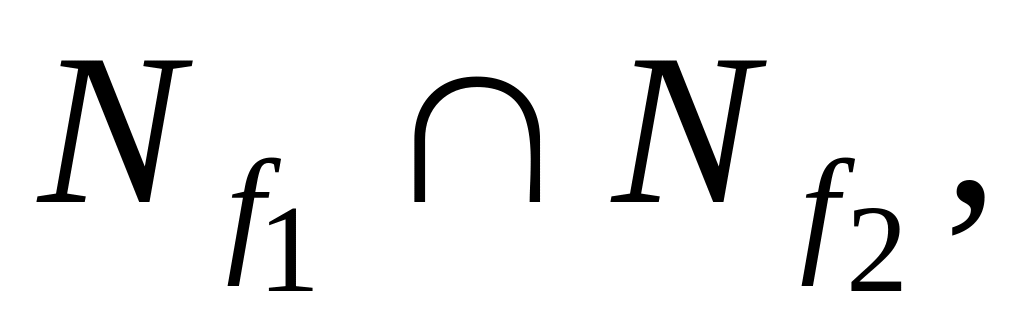
функции
 соответствует подмножество
соответствует подмножество
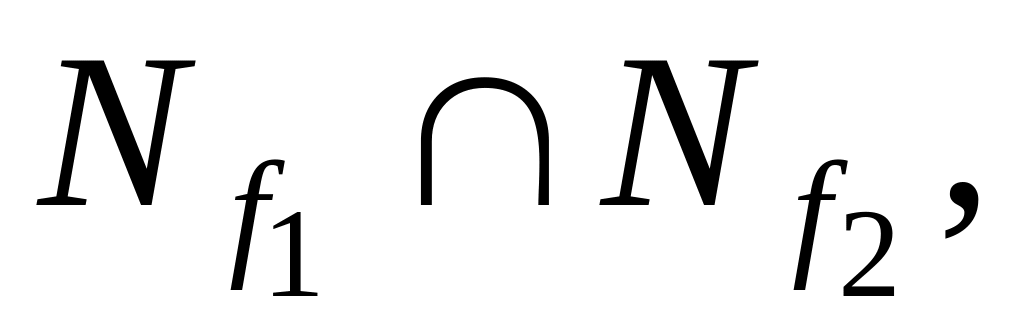
если
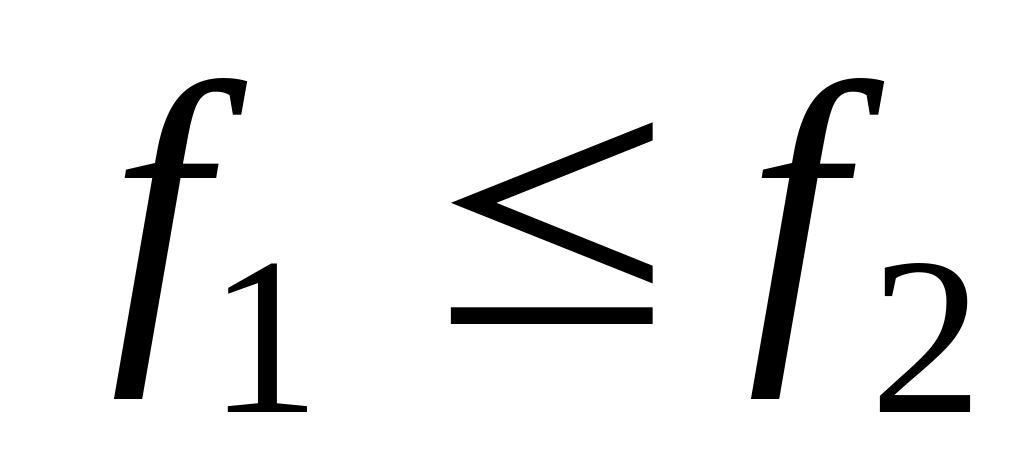 , то
, то
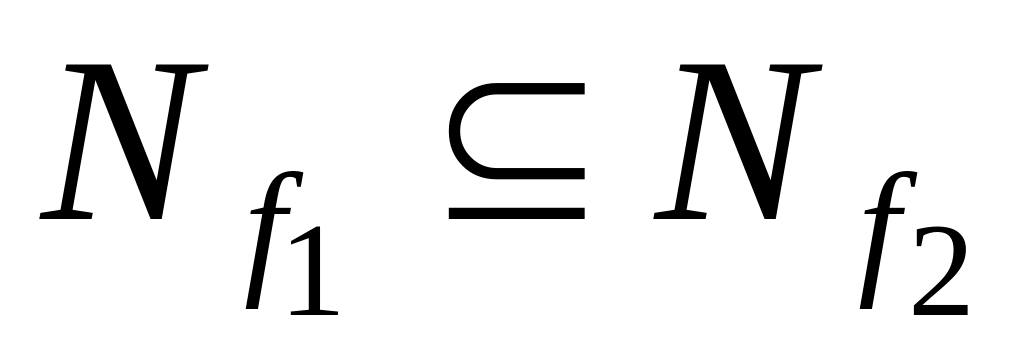 .
.
Подмножество
![]() называется интервалом
-го
ранга, если оно соответствует элементарной
конъюнкции
K
r
- го ранга.
называется интервалом
-го
ранга, если оно соответствует элементарной
конъюнкции
K
r
- го ранга.
Таким образом, каждая вершина единичного куба является интервалом n-го ранга, множество всех вершин – интервалом нулевого ранга, а интервал n-го ранга геометрически представляет собой подмножество вершин куба, заполняющих (n-r) – мерную грань.
Для
каждой д.н.ф.
![]() функции
выполняется соотношение
функции
выполняется соотношение
![]() .
.
Поэтому
с каждой д.н.ф. функции
связано покрытие подмножества
![]() интервалами
интервалами
![]() такими,
что
такими,
что
![]() .
.
Справедливо и обратное положение.
Обозначим
через
![]() ранг интервала
ранг интервала
![]() .
Тогда
.
Тогда
![]() совпадает с числом букв в д.н.ф.
совпадает с числом букв в д.н.ф.
Таким образом , задача построения минимальной д.н.ф. сводится к отысканию такого покрытия интервалами , чтобы выражение было минимальным. При построении покрытия , соответствующего кратчайшей д.н.ф., следует минимизировать число интервалов, участвующих в покрытии.
Интервалы
![]() ,
для которых
,
для которых
![]() ,
будем называть допустимыми также, как
и соответствующие им конъюнкции.
,
будем называть допустимыми также, как
и соответствующие им конъюнкции.
Сокращенная д.н.ф.
Интервал
называется
максимальным для f,
если
и не существует интервала
![]() такого , что
такого , что
![]() .
Очевидно, что каждый интервал
содержится
в некотором максимальном интервале
.
Поэтому совокупность всех максимальных
для f
интервалов
определяет покрытие подмножества
,
.
.
Очевидно, что каждый интервал
содержится
в некотором максимальном интервале
.
Поэтому совокупность всех максимальных
для f
интервалов
определяет покрытие подмножества
,
.
Д.н.ф.
![]() ,
реализующая функцию f
и
соответствующая покрытию подмножества
всеми
максимальными для f
интервалами, называется сокращенной
д.н.ф. функции f
. Функции f
будем обозначать ее через
,
реализующая функцию f
и
соответствующая покрытию подмножества
всеми
максимальными для f
интервалами, называется сокращенной
д.н.ф. функции f
. Функции f
будем обозначать ее через
![]() Сокращенная д.н.ф. определяется по
функции f
однозначно.
Сокращенная д.н.ф. определяется по
функции f
однозначно.
Теорема. Минимальная д.н.ф. функции получается из сокращенной д.н.ф.
функции путем удаления некоторых элементарных конъюнкций .
Следствие. Если конъюнкция К не входит а сокращенную д.н.ф. функции , то К не входит нив одну минимальную д.н.ф. для .
Теорема. Для всякой функции существует кратчайшая д.н.ф., которая получается из сокращенной д.н.ф. функции путем удаления некоторых элементарных конструкций .
Теорема. Сокращенная д.н.ф. монотонной функции не содержит отрицаний переменных и является ее единственной минимальной (кратчайшей) д.н.ф.
Методы построения сокращенной д.н.ф.
В основе этих методов лежат следующие преобразования :
1)
склеивание ![]() ,
,
2)
поглощение ![]() ,
,
3)
неполное склеивание ![]() ,
,
4)
обобщенное склеивание ![]() .
.
(операции 1), 3) можно выразить через 2) , 4) )
Метод Блейка
Метод использует операции поглощения и обобщенного склеивания .
Сначала выполняются все возможные преобразования 4).
После того как получены все конъюнкции , соответствующие максимальным интервалам , преобразование 2) удаляет все конъюнкции , соответствующие не максимальным интервалам. В результате получится сокращенная д.н.ф. Заметим , что порядок выполнения операций не существен.
Тупиковые д.н.ф.
Покрытие подмножества максимальными интервалами называется неприводимым, если после удаления из него любого интервала оно перестает быть покрытием.
Д.н.ф. функции называется тупиковой , если ей соответствует неприводимое покрытие подмножества .
Очевидно, что всякая минимальная (кратчайшая) д.н.ф. является тупиковой.
Заметим, что если сокращенная д.н.ф. по функции строится однозначно, то процесс перехода от сокращенной д.н.ф. к тупиковой неоднозначен. При этом удаление одних элементарных конъюнкций из сокращенной д.н.ф. приводит к минимальной д.н.ф., других - к тупиковой д.н.ф , не являющейся минимальной .
Процесс построения минимальных(кратчайших)д.н.ф. на основе совершенной д.н.ф можно описать следующим образом : строится сокращенная д.н.ф. , затем строятся все тупиковые д.н.ф. и среди них выделяются минимальные (сокращенные) д.н.ф.
