
- •Понятие дискретного источника сообщений.
- •Первая и вторая теорема Шеннона для источников без памяти
- •Оптимальное кодирование. Основные понятия и определения.
- •Однозначная декодируемость неравномерного кода.
- •Методы построения префиксных кодов. Метод Шеннона.
- •Свойства оптимального кода.
- •Алгоритм Хаффмана.
- •Блоковые коды
- •Линейные коды.
- •Эквивалентные и систематические коды.
- •Стандартное расположение.
- •Декодирование с использованием синдромов.
- •Последовательное декодирвание.
- •Методы построения новых кодов. Методы: добавление общей проверки на четность; выкалывание кодовых координат.
- •Определения
Последовательное декодирвание.
Теорема: Пусть код, используемый для передачи по ДСК, пусть все кодовый векторы имеют одну вероятность быть переданными, тогда средняя вероятность правильного декодирования совпадает с наибольшей возможной вероятностью для этого кода, если в качестве таблицы декодирования используется стандартное расположение, в котором каждый образующий вектор смежного класса имеет минимальный вес в своем классе.
Вес смежного класса это вес минимального по весу элемента в данном смежном классе.
В некоторых
случая для линейных кодов по полученному
вектору
удается находить минимальный вес
элемента смежного класса, содержащего
.
В этом случае декодирование осуществляется
так: пронумеруем элементы поля Галуа с
системой исчисления q,
номерами
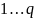 ,
так чтобы нулевой элемент был последним
,
так чтобы нулевой элемент был последним
 ,
,
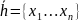 .
Найдем вес смежного класса
.
Найдем вес смежного класса
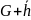 ,
затем заменим
,
затем заменим
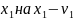 и т.д. Найдем веса смежных классов,
содержащих полученный вектор с измененными
координатами
и т.д. Найдем веса смежных классов,
содержащих полученный вектор с измененными
координатами
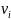 -элементы
поля, приводящие к максимальному
уменьшению веса. Пусть
-элементы
поля, приводящие к максимальному
уменьшению веса. Пусть
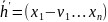 ,если
смещение
не произошло, то будем рассматривать
полученный вектор
,
проделываем процедуру уменьшения
последовательно с остальными координатами
вектора. В итоге будет получен вектор,
принадлежащий смежному классу веса 0,
т.е. самому коду
,если
смещение
не произошло, то будем рассматривать
полученный вектор
,
проделываем процедуру уменьшения
последовательно с остальными координатами
вектора. В итоге будет получен вектор,
принадлежащий смежному классу веса 0,
т.е. самому коду
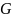 .
Построенный кодовый вектор считается
вектором, переданным по каналу связи,
а описанная процедура называется
процедурой
последовательного декодирования.
.
Построенный кодовый вектор считается
вектором, переданным по каналу связи,
а описанная процедура называется
процедурой
последовательного декодирования.
Проверочная матрица кода Хэмминга.
Процедура декодирования кодов Хэмминга.
Двоичный симплексный код к коду Хэмминга.
Является
методом построения двоичного кода
исправляющего 1 ошибку. Синдром, принятого
вектора
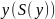 равен линейной комбинации тех столбцов
проверочной матрицы (
)
номера которых совпадают с номерами
искаженных компонент, а коэффициенты
линейной комбинации равны величинам
ошибок, поэтому проверочная матрица
кода исправляющего ошибку должна
удовлетворять 2-м ограничениям:
равен линейной комбинации тех столбцов
проверочной матрицы (
)
номера которых совпадают с номерами
искаженных компонент, а коэффициенты
линейной комбинации равны величинам
ошибок, поэтому проверочная матрица
кода исправляющего ошибку должна
удовлетворять 2-м ограничениям:
Матрица H не должна иметь 0 столбцов.
Все столбцы матрицы должны быть различными.
В противном случае ошибки не будут выявляться.
Пусть
 число строк проверочной матрицы
число строк проверочной матрицы
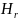 .
Чтобы построить код с максимально
возможной скоростью передачи данных
(
)
возьмем все допустимые не нулевые
двоичные векторы столбцы из векторного
пространства
.
Чтобы построить код с максимально
возможной скоростью передачи данных
(
)
возьмем все допустимые не нулевые
двоичные векторы столбцы из векторного
пространства
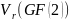 ,
для построения матрицы
,
для построения матрицы
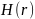 будем выписывать их в порядке возрастания
чисел.
будем выписывать их в порядке возрастания
чисел.
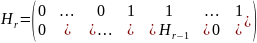
Двоичный
код с длиной блока
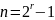 проверочной матрицы
проверочной матрицы
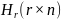 образованный всеми не нулевыми векторами
из векторного пространства
,
расположенными в порядке возрастания
чисел, двоичные разложения которых
совпадают с рассматриваемыми столбцами
называется двоичным
кодом Хемминга.
Обозначается
.
образованный всеми не нулевыми векторами
из векторного пространства
,
расположенными в порядке возрастания
чисел, двоичные разложения которых
совпадают с рассматриваемыми столбцами
называется двоичным
кодом Хемминга.
Обозначается
.
Длина
кодового слова
;
количество информационных символов
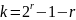 .
.
Процедура
декодирования для кодов Хемминга имеет
вид: пусть произошла ошибка в
символе кодового слова
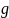 ,
подсчитаем синдром полученного вектора
,
подсчитаем синдром полученного вектора
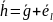 .
Тогда синдром будет иметь вид
.
Тогда синдром будет иметь вид
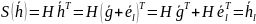 .
Если произошла 1 ошибка, то синдром в
двоичной записи указывает номер столбца,
в котором произошла ошибка. Из свойств
кода исправлять ошибку следует, что
кодовое расстояние
.
Если произошла 1 ошибка, то синдром в
двоичной записи указывает номер столбца,
в котором произошла ошибка. Из свойств
кода исправлять ошибку следует, что
кодовое расстояние
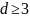 .
.
Теорема: коды Хемминга являются совершенными.
Коды
Хемминга распространяются на любую
систему счисления. Длина кода
характеризуется числом
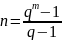 ,
где
,
где
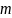 -
число строк проверочной матрицы и
-
число строк проверочной матрицы и
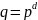 ,
,
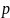 -простое
число.
-простое
число.
Двоичным
симплексным кодом ( )
называют код, двойственных коду Хемминга.
По определению двойственного кода
порождающая матрица кода Хемминга
является проверочной для двоичного
симплексного кода, проверочная матрица
кода Хемминга
является порождающей для двоичного
симплексного кода. Для построения
двоичного симплексного кода используют
индуктивный метод.
)
называют код, двойственных коду Хемминга.
По определению двойственного кода
порождающая матрица кода Хемминга
является проверочной для двоичного
симплексного кода, проверочная матрица
кода Хемминга
является порождающей для двоичного
симплексного кода. Для построения
двоичного симплексного кода используют
индуктивный метод.
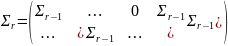
Каждая
пара кодовых слов симплексного кода
находится друг от друга на одинаковом
расстоянии, такие коды называются
эквидистантными. Все
слова симплексного кода, за исключением
нулевого, имеют одинаковый вес, т.е.
симплексный код является равновесным.
Симплексные коды распространяются на
все системы счисления. Параметры кода:
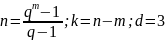
– число проверочных символов
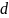 – кодовое расстояние
– кодовое расстояние
