
- •Понятие дискретного источника сообщений.
- •Первая и вторая теорема Шеннона для источников без памяти
- •Оптимальное кодирование. Основные понятия и определения.
- •Однозначная декодируемость неравномерного кода.
- •Методы построения префиксных кодов. Метод Шеннона.
- •Свойства оптимального кода.
- •Алгоритм Хаффмана.
- •Блоковые коды
- •Линейные коды.
- •Эквивалентные и систематические коды.
- •Стандартное расположение.
- •Декодирование с использованием синдромов.
- •Последовательное декодирвание.
- •Методы построения новых кодов. Методы: добавление общей проверки на четность; выкалывание кодовых координат.
- •Определения
Блоковые коды
Блоковые
коды: В кодере,
предназначенном для блоковых кодов,
непрерывная последовательность
информационных символов разбивается
на отрезки, содержащие по k
символов или на k
значные блоки. В дальнейшем операции
проводятся над каждым блоком отдельно,
не зависимо от других. Каждому
информационному блоку из k
символов сопоставляется набор из n-k
символов, где n>k
и называются проверочные символы. Набор
n
символов, составленный из k
информационных и n-k
проверочных, называется кодовым
словом. Кодовое слово
передается по каналу связи, искажается
шумом, а затем декодируется независимо
от других кодовых слов. n
– длина блока. Совокупность всех кодовых
слов называется кодом.
Мощность кодового алфавита
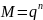 ,
где q
– основание кода, n
– длина кодового слова.
,
где q
– основание кода, n
– длина кодового слова.
Компоненты кодовых слов являются элементами поля Галуа. Часто рассматриваются двоичные коды.
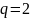 рассмотрим двоичный
симметричный канал (ДСК), предназначенный
для передачи двоичной информации.
Предположим, что сигналы передаются
независимо, шум накладывается на
передаваемую информацию. На примере
ДСК покажем основной принцип декодирования.
рассмотрим двоичный
симметричный канал (ДСК), предназначенный
для передачи двоичной информации.
Предположим, что сигналы передаются
независимо, шум накладывается на
передаваемую информацию. На примере
ДСК покажем основной принцип декодирования.
q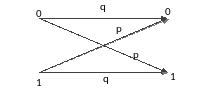 - вероятность совпадения переданного
и принятого символа
- вероятность совпадения переданного
и принятого символа
p – вероятность искажения передаваемого символа
q>p – плохой канал
q>>p – хороший канал
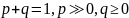
 -вероятность
того, что при передаче не произойдет
ошибок.
-вероятность
того, что при передаче не произойдет
ошибок.
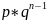 -
вероятность, что произойдет 1 ошибка и
т.д.
-
вероятность, что произойдет 1 ошибка и
т.д.
Т.к. q>p, то численные значения убывают.
В предположении, что все слова кода имеют одинаковую вероятность быть переданными по каналу, наилучшим решением на приемнике будет декодирование в такое кодовое слово, которое отличается от полученного в наименьшем числе компонент, т.е. декодирование в ближайшее кодовое слово. Такое декодирование называется декодированием по методу максимального правдоподобия.
Количество единиц, в кодовом слове, называется весом слова и обозначается W(q).
Расстоянием
Хемминга между 2-я кодовыми словами
определяется как число компонент, в
которых эти слова отличаются друг от
друга ( ,
,
 -
вес вектора).
-
вес вектора).
При искажении t компонент у некоторого кодового слова полученное на выходе канала слово будет отличаться от переданного в t компонентах, т.е. будет удалено на расстояние t.
Условиями, для обнаружения и исправления ошибок являются:
Для обнаружения всех комбинаций из d-1 или меньшего числа ошибок необходимо и достаточно, чтобы минимальное расстояние Хемминга между кодовыми словами было равно d.
Для того чтобы исправить все комбинации из t или меньшего числа ошибок необходимо и достаточно, чтобы минимально расстояние между кодовыми словами было равно 2t+1.
Линейные коды.
Линейные
коды: Пусть
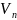 n-
мерное векторное пространство над полем
Галуа
n-
мерное векторное пространство над полем
Галуа
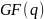 ,
подпространство
,
подпространство
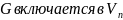 называется линейным
блоковым кодом.
называется линейным
блоковым кодом.
Величина
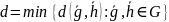 называется кодовым расстоянием.
называется кодовым расстоянием.
Расстояние
между 2-мя кодовыми словами линейного
блокового слова равно весу некоторого
не нулевого кодового слова, т.к.

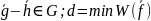 .
.
Кодовое расстояние для линейного блокового кода равно минимальному весу его не нулевых кодовых слов.
Пример:
q=2;
n=5;
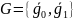 ;
;
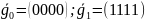
Код предназначен для кодирования двоичной информации. Его характеристики: большая помехозащищенность и малая скорость передачи информации. Этот код называется кодом кратных повторений.
Пусть G
подмножество
– линейный код размерности k.
Матрица
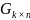 составленная из базисных векторов
подпространства Gназывается
порождающей матрицей кода G.
составленная из базисных векторов
подпространства Gназывается
порождающей матрицей кода G.
Для
линейного кода G
размера k
с кодовым расстоянием d
используется обозначение
 -
код. Этот код содержит
-
код. Этот код содержит
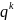 векторов. Поэтому код можно описать
перечислением всех кодовых слов, а можно
использовать более компактный способ
с помощью порождающей матрицей G.
векторов. Поэтому код можно описать
перечислением всех кодовых слов, а можно
использовать более компактный способ
с помощью порождающей матрицей G.
Из курса геометрии известно, что подпространство векторного пространства может быть задано различными базисами, что обуславливает неоднозначность выбора порождающей матрицы кода.
Векторы
 называются ортогональными если
называются ортогональными если
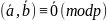 .
.
Пусть G векторное подпространство размерности k множество всех векторов из ортогональных к G образуют ортогональное векторное пространство.
Существует
матрица
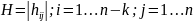 ранга n
ранга n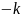 ,строками
которой является базис ортогонального
подпространства.
,строками
которой является базис ортогонального
подпространства.
Вектор
 ,когда
ортогонален каждой строке матрицы
,когда
ортогонален каждой строке матрицы
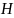 (
(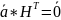 ).
В координатной записи это соотношение
имеет вид
).
В координатной записи это соотношение
имеет вид
 .
Эти формулы означают, что компоненты
кодового слова должны удовлетворять
совокупности n-k линейно независимых
уравнений, эти уравнения называются
обобщенными проверками
на четность. Соотношение
проверок на четность должны выполняться
и для базисных векторов подпространства
G
(
.
Эти формулы означают, что компоненты
кодового слова должны удовлетворять
совокупности n-k линейно независимых
уравнений, эти уравнения называются
обобщенными проверками
на четность. Соотношение
проверок на четность должны выполняться
и для базисных векторов подпространства
G
(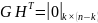 ).
).
Ортогональное
подпространство с порождающей матрицей
H
называется линейным
n-k
кодом, двойственным к линейному (n,k)
кода
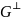 .
.
Пусть G
– линейный (n,k)
код с проверочной матрицей H,
тогда каждому кодовому слову
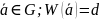 соответствует соотношение линейной
зависимости связывающей d
столбцов матрицы H.
Каждому соотношению линейной зависимости
включающей d
столбцов матрицы H
соответствует кодовое слово веса d.
соответствует соотношение линейной
зависимости связывающей d
столбцов матрицы H.
Каждому соотношению линейной зависимости
включающей d
столбцов матрицы H
соответствует кодовое слово веса d.
Блоковый код являющийся ортогональным пространством матрицы H имеет минимальный вес равный самое меньшее d тогда и только тогда, когда любая совокупность d -1 и меньшего числа столбцов матрицы H является линейно независимой.
Вероятностью
ошибки декодирования для данной схемы
декодирования называется вероятность
появления кодового слова на выходе
декодера отличного
от переданного в канал связи. Если все
кодовые слова используются с равной
вероятностью, вероятность ошибки
декодирования
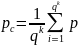 .
Для любого канала с независимыми
ошибками, 2 кода отличающиеся расположением
символов имеют одну и ту же вероятность
ошибки.
.
Для любого канала с независимыми
ошибками, 2 кода отличающиеся расположением
символов имеют одну и ту же вероятность
ошибки.
