Первая и вторая теорема Шеннона для источников без памяти

Первая теорема Шеннона

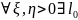такое, что при l>l₀ все реализации длины l источника [A, p(S)] могут быть разбиты на 2 класса

таких, что для последовательности 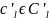имеет место неравенство

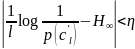
Где – энтропия источника.

Суммарная вероятность последовательностей из 2-го класса <ε

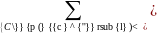
Следствие 1) Оценивается:

, а – основание логарифма

Следствие 2) Суммарная вероятность последней из первого класса не менее 1-ε:

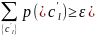
Упорядочим все последовательности длины l, полученные из источника без памяти, по убыванию их вероятностей. Пусть 0<α<1. Будем отбирать наиболее вероятные последовательности, пока их суммарная вероятность, оставаясь меньше заданного α, не будет обладать следующим свойством: добавление у этой сумме вероятности реализации следующей последовательности делает её больше α. Множество отобранных последовательностей обозначим M_I(α).

Вторая теорема Шеннона.

Для класса M_I(α) высоковероятных последовательностей, реализуемых на источнике без памяти [A, p(S)], определяемого заданным уровнем α: 0<α<1 имеет место следующее равенство:

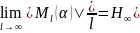
Геометрическая интерпретация распределения вероятностей на множестве реализаций и последовательностей ИБП.

Марковские источники.

Дискретный стационарный источник называется Марковским порядка m, если для любого 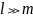и любой последовательности 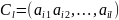выполняется, что вероятность появления .

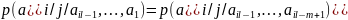Последовательность является реализацией конечной стационарной цепи Маркова с глубиной зависимости M.

Шаговая энтропия Марковского источника периода k:

Энтропия источника на 1 знак:

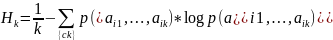
Связь между и устанавливает равенство:

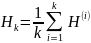
Последовательность является не возрастающей для .

Энтропией Марковского источника называется величина:

Энтропия Марковского источника всегда существует в силу теоремы Вейер-Штрасса.

Теоремы Шеннона для Марковских источников.

1 теорема Шеннона для Марковских источников.

m=1.

Для любых 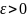и существует 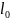такое, что при все реализации длины 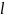источника могут быть разбиты на 2 класса

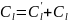
Энтропия источника: причем

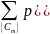
2 теорема Шеннона для Марковских источников

Для любых и существует такое, что при все реализации длины источника могут быть разбиты на 2 класса

Энтропия источника:

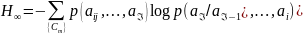
Марковский источник обладает свойством информационной устойчивости, что позволяет оценить число последних вошедших в 1-ый класс.

Эргодические источники

(*)

Дискретный стационарный источник [A,p(s)] называется эргодическим, если любое измеримое относительно вероятностной меры p(s), заданной на Fs, инвариантное по сдвигу множество последовательностей, порождённых источником, имеет вероятность либо единица, либо нуль.

Эргодические источники являются наиболее близкими с вероятностной точки зрения моделями осмысленных сообщений. Поэтому формулу (*) можно рассматривать как оценку числа литературных текстов длины l, в алфавите А, где H∞ понимается как энтропия текста на один знак.

Теоремы Мак-Милана.

Пусть последовательность C_l порождена дискретным стационарным эргодическим источником [A,P (S)] . Тогда для произвольных ε>0, δ>0 существует целое число l₀(ε, δ) такое, что при l> l₀(ε, δ)

(1)

Где p(c_l) – вероятность реализации последовательности

c_l =a_i1,…, a_il, а H∞- энтропия источника.

Доказательство:

для любого ε > 0 и соответствующего δ’ > 0 для m > m₀(ε) и l > m будет выполняться:

на любителя:

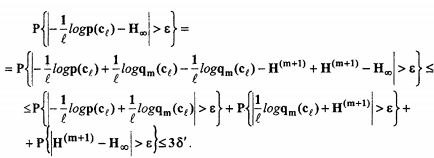
Полагая δ’= δ/3 получаем, что для достаточно больших l будет выполняться неравенство (1), что и доказывает теорему Мак-Миллана.

Имеет место свойство информационной устойчивости. Собственная информация последовательности, порождённой эргодическим стационарным источником, удовлетворяет соотношению:

Используем эту вероятностную трактовку соотношения. Последовательности, порождённые стационарным эргодическим источником, обладают свойством равнораспределённости

Свойство равнораспределённости позволяет оценить количество последовательностей, порождённых источником такого типа:

(*)