Методы построения префиксных кодов. Метод Шеннона.

Метод Шеннона

1. Упорядочиваем буквы алфавита А по убыванию их вероятностей.

2. Находит числа l_i, i=1,…,n, исходя из условий

3. Подсчитываем накопленные суммы. P₁=0, P₂=P(a₁),P₃=P(a₁)+P(a₂),

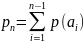
4. Находим первые после запятой l_iзнаков в разложении числа P_iв двоичную дробь. Цифры этого разложения, стоящие после запятой, являются кодовым словом соответствующим букве a_i

5. Если необходимо, провести операцию усечения.

При переводе правильной дроби в систему счисления с основание q необходимо сначала саму дробь , а затем и дробные зачти всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения. Умножение производить до тех пор, пока дробная часть произведений не станет равна нулю. Это означает, что сделан очный перевод. В противном случае - перевод осуществляется до заданной точности.

Свойства оптимального кода.

Свойства оптимального кода: Рассмотрим источник кодирования, с вероятностями 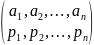, причем 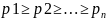.Необходимо построить двоичный код с минимальной средней длиной.

Рассмотрим свойства оптимального кода для вероятностных распределений на алфавите А, отличного от равномерного.

Свойства:

1. В оптимальном коде длины 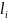кодовых слов не убывают.

2. Существует оптимальный префиксный код, в котором двум, наименее вероятным буквам 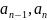, соответствуют кодовые слова, имеющие одинаковую длину и различающиеся лишь в последнем разряде.

Построим новый источник A’, полученный из исходного источника A склеиванием наименее вероятных букв в букву a’ в источнике A’. Буквы 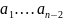порождаются с вероятностями совпадающими с вероятностями этих букв в источнике A, а буква a’ имеет вероятность равную сумме вероятностей ( ). Новый источник называется редуцированным, а операцию его получения редуцированием, эту операцию можно проводить конечное число раз, до тех пор, пока алфавит источника не будет состоять из 1 буквы, порождаемой с вероятностью 1. Имея код, отвечающий редуцированному источнику A’ можно построить код, отвечающий исходному источнику А.

Пусть буквам алфавита A’ сопоставлены кодовые слова 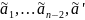тогда для алфавита A построим код следующим образом: для букв 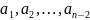сохраним кодовые слова , а в качестве 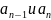кодовых слов возьмём слова, полученные в результате дописывания к кодовому слову символов 0 и 1 соответственно.

3. Если префиксный код, для редуцированного источника A’, является оптимальным, то и код, для исходного источника A, построенного указанным способом, также будет оптимальным.

Алгоритм Хаффмана.

Алгоритм Хаффмана для двоичной системы исчисления (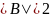 ): Этот алгоритм приводит к построению оптимального множества кодовых слов, в том смысле, Что никакое другое множество не имеет меньшего среднего числа символов на букву алфавита А. Для любого источника все наборы кодовых слов, удовлетворяющие свойствам 1-3, дают одну и ту же среднюю длину кодового слова. Этот алгоритм позволяет построить, по крайней мере, один из таких наборов. Последовательная реализация свойств 1-3 и есть суть метода Хаффмана.

Алгоритм Хаффмана сводится к выполнению 2-х частей алгоритма:

1. Построение последовательностей редуцированных источников сходящихся к вырожденному источнику.

1. Буквы источника располагают в порядке убывания вероятностей.

2. Две наименее вероятные буквы склеиваются в 1 букву редуцированного источника и приписывают этой букве суммарную вероятность склеенных букв.

3. Переходят к 1-у пункту, если алфавит редуцированного источника состоит из 2-х или более букв, в противном случае переходят ко 2-ой части.

2. Построение кодового дерева и соответствующего оптимального кода.

Проводят ребра, соединяющие буквы в алфавитах последовательных редуцированных источников и получаем граф дерева, в котором буквы исходного источника являются концевыми вершинами дерева, а единственная буква последнего вырожденного источника соответствует корню дерева. Помечают построенные ребра метками из алфавита 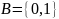и прослеживают эти метки при движении от корня дерева к концевой вершине. В итоге получают кодовое слово, соответствующее букве исходного алфавита. Полученный код является префиксным.

Приведенный алгоритм приводит к оптимальному множеству кодовых слов, за исключением, когда в исходном источнике или последующих редуцированных источниках имеется более 2-х букв с равными и минимальными вероятностями. Располагая в другом порядке буквы редуцированных алфавитов можно получить оптимальные префиксные коды с наборами кодовых слов тех же длин, что и в рассмотренном примере, коды будут отличаться лишь кодовыми словами.

Теоремы о возможности сжатия информации при кодировании.

1. Рассматривается источник без памяти с энтропией, возможно, так закодировать буквы, порождённые этим источником по средствам префиксного кода, составленного в алфавите B, что среднее число символов на букву 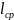удовлетворяет неравенству

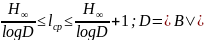
Данная теорема позволяет привести интерпретацию энтропии источника в случае, когда среднее число двоичных символов алфавита B, требуемых для кодирования буквы, порожденных источником, не меньше энтропии источника и не превосходит энтропию этого источника более чем на 1.

2. Введем коэффициент сжатия, обобщающий понятие средней длины кодового слова. Пусть 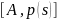марковский источник с энтропией , порождающий последовательность 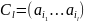, 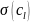–длина соответствующего кодового слова, коэффициентом сжатия последовательности длины назовем величину .

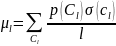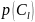- вероятность последовательности

–длина кодового слова этой последовательности

При

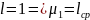
– коэффициент сжатия кода.

Теоремы о кодировании источников без памяти.

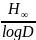Точная нижняя грань коэффициента по всем возможным однозначно декодируемым кодам равняется . Для любого возможного способа кодирования нельзя добиться большего сжатия, чем указанная величина.

Задача помехоустойчивого кодирования

Обобщенная схема цифровой аналоговой связи может быть представлена следующим образом:

Кодер – устройство преобразования информации, предназначенной для передачи по каналу связи.

Декодер – преобразует сигналы, полученные на выходе канала связи в информацию, предназначенную для получателя.

Для хранения информации используются диски, магнитные элементы и т.д.

Сигналы поступают в канал и искажаются шумом, искаженные сигналы поступают в декодер, который восстанавливает посланное сообщение и направляет его получателю.

Основная задача в технике связи заключается в построении кодера и декодера для надежной передачи информации.

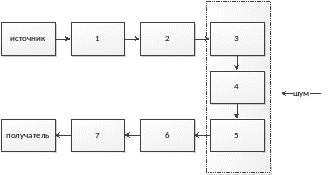
1 – кодер, кодирующий входную информацию в двоичные сигналы

2 – кодер, кодирующий двоичные сигналы

3 – кодер, кодирующий двоичные сигналы в сигналы на входе в канал.

4 – канал связи или память

5 – декодер, декодирующий сигналы на выходе канала в двоичные символы (демодулятор)

6 - декодер – исправляет ошибки в двоичных символах

7- декодер, декодирующий двоичные символы в сообщение.

Математическое описание функционирования кодера (2) и декодера (6), обеспечивающих заданный уровень надежности передачи информации.

В идеальной системе связи искажение в канале отсутствует, однако в реальной системе всегда имеются случайные ошибки. Поэтому для обнаружения или исправления таких ошибок используют корректирующие коды. Эти коды не могут исправлять любую возможную комбинацию ошибок, их задача исправлять наиболее правдоподобные комбинации ошибок. В основу построения корректирующих кодов положено предположение, что каждый символ искажается шумом не зависимо остальных искажений и, следовательно, вероятность данной комбинации ошибок зависит только от числа ошибок. Это предположение искусственно, т.к. в реальных ситуациях время действия помехи превышает продолжительность передачи 1 символа. Следовательно, необходимы коды для исправления серий ошибок.

В рамках теории информации мы будем рассматривать коды “корректирующей изолированной ошибки”.

Говорят, что код обнаруживает ошибку, если декодер сигнализирует об отличии принятого вектора от переданного кодового слова. Говорят, что код исправляет ошибку, если декодер указывает позицию и значение искаженной координаты.