
- •Понятие дискретного источника сообщений.
- •Первая и вторая теорема Шеннона для источников без памяти
- •Оптимальное кодирование. Основные понятия и определения.
- •Однозначная декодируемость неравномерного кода.
- •Методы построения префиксных кодов. Метод Шеннона.
- •Свойства оптимального кода.
- •Алгоритм Хаффмана.
- •Блоковые коды
- •Линейные коды.
- •Эквивалентные и систематические коды.
- •Стандартное расположение.
- •Декодирование с использованием синдромов.
- •Последовательное декодирвание.
- •Методы построения новых кодов. Методы: добавление общей проверки на четность; выкалывание кодовых координат.
- •Определения
Стандартное расположение.
Пусть G
(n,k)
код,
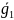 нулевой вектор,
нулевой вектор,
 остальные кодовые векторы. Процедура
декодирования веторов из векторного
пространства
полученных на выходе канала основана
на следующей таблице расположения
векторов n
мерного векторного пространства. Кодовые
векторы расположены в строке с нулевым
вектором слева, затем один из оставшихся
векторов т мерного векторного пространства,
например
остальные кодовые векторы. Процедура
декодирования веторов из векторного
пространства
полученных на выходе канала основана
на следующей таблице расположения
векторов n
мерного векторного пространства. Кодовые
векторы расположены в строке с нулевым
вектором слева, затем один из оставшихся
векторов т мерного векторного пространства,
например
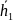 помещаем под нулевым вектором
,
Обычно в качестве
выбирают вектор минимального веса, т.к.
такой вектор наиболее вероятно получить
на выходе, если по каналу передавался
нулевой вектор. Вторая строка заполняется
так, чтобы под каждым кодовым вектор
помещаем под нулевым вектором
,
Обычно в качестве
выбирают вектор минимального веса, т.к.
такой вектор наиболее вероятно получить
на выходе, если по каналу передавался
нулевой вектор. Вторая строка заполняется
так, чтобы под каждым кодовым вектор
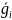 находился вектор
находился вектор
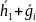 .
Аналогично в первый столбец следующей
строки помещают вектор
.
Аналогично в первый столбец следующей
строки помещают вектор
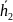 минимального веса и не вошедший в
предыдущие строки таблицы. Процесс
продолжается, пока каждый вектор из
пространства
не
появится в какой либо из строк таблицы.
минимального веса и не вошедший в
предыдущие строки таблицы. Процесс
продолжается, пока каждый вектор из
пространства
не
появится в какой либо из строк таблицы.
Расположение векторов n мерного векторного пространства в виде таблицы таблица… называется стандартным расположением.
В каждой
строке
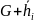 таблицы
находятся векторы смежного класса, n
мерного векторного пространства по
подпространству G.
В первом столбце находятся образующие
классов смежности. При соответствующем
выборе этих образующих процедура
декодирования с использованием
стандартного расположения векторов n
мерного векторного пространства обладает
свойствами:
таблицы
находятся векторы смежного класса, n
мерного векторного пространства по
подпространству G.
В первом столбце находятся образующие
классов смежности. При соответствующем
выборе этих образующих процедура
декодирования с использованием
стандартного расположения векторов n
мерного векторного пространства обладает
свойствами:
/* Вектор
ошибок
 ,
если по каналу связи был послан вектор
,
если по каналу связи был послан вектор
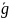 ,
а получен
,
а получен
 . */
. */
Если
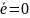 ,
то ошибок не произошло. Если
,
то ошибок не произошло. Если
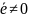 ,
то
,
то
не нулевые компоненты вектора ошибок
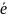 соответствуют искаженным компонентам
кодового вектора
;
соответствуют искаженным компонентам
кодового вектора
;Если стандартное расположение n мерного векторного пространства используется как таблица декодирования для линейного кода, то по полученному вектору будет правильно декодирован когда является образующим смежного класса.
Декодирование с использованием синдромов.
Декодирование
полученного вектора
с использование таблицы стандартного
расположения осуществляется следующим
образом: пусть
находится в i-ой
строке, тогда из него вычитается вектор
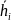 образующей этого класса смежности.
образующей этого класса смежности.
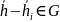 – переданный кодовый вектор.
– переданный кодовый вектор.
Данный
метод декодирования является простым,
но для его реализации требуется большая
память (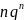 ).
).
Рассмотрим модификацию этого метода.
Пусть
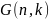 ортогональное пространство матрицы
ортогональное пространство матрицы
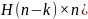 .
.
Для любого,
полученного на выходе канала вектора
,
тогда
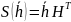 -синдром.
-синдром.
Т.к.
пространство ортогональное, то
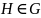 ,
когда
,
когда
 .
.
Два вектора
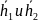 принадлежат одному и тому же классу
смежности, когда их синдромы равны.
принадлежат одному и тому же классу
смежности, когда их синдромы равны.
Т.о. процесс
декодирования можно упростить за счет
использования таблицы соответствия
образующих смежного класса и синдромов
для каждого класса смежности. Классов
смежности:
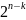 .
.
После
того как на выходе канала получим
,
вычисляется его синдром, затем по таблице
отыскивается соответствующий ему вектор
образующий смежного класса, который
является предполагаемым набором ошибок.
Вычитание его из
дает, предположительно, посланный
кодовый вектор. Объем памяти, требуемый
для декодирования с использованием
синдромов равен
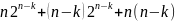 .
.
