Эквивалентные и систематические коды.
Эквивалентные и систематические коды: Коды, отличающиеся перестановкой столбцов, в порождающей матрице называются эквивалентными.
Назовем 2 порождающие матрицы комбинаторно эквивалентными, если одна из другой может быть получена путем элементарного преобразования строк и перестановкой столбцов.
Линейный
блоковый
кода G
называется систематическим, если первые
k
компонент каждого кодового слова
являются информационными, а последние
n-k
компоненты проверочными символами.
Теорема: Каждый линейный блоковый код эквивалентен систематическому коду.
Если порождающая матрица кода имеет приведенную форму, то одна из проверочных матриц может быть легко найдена.
Теорема:
если G
систематический код с порождающей
матрицей
,
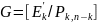где
единичная матрица, а
матрица порядка
,
то проверочная матрица имеет вид
.
Задача оптимизации кодов.
Задачи оптимизации кодов.
Из свойств обнаружения всех комбинаций ошибок следует, что способность кода корректировать ошибки находятся в прямой зависимости от величины кодового расстояния. Хорошие корректирующие свойства обеспечиваются большим кодовым расстоянием и наоборот. Для построения кодов с большим кодовым расстоянием требуется вводить много проверочных символов, не передающих информацию от источника к адресату, а выполняющих вспомогательную роль. Наличие большого числа проверочных символов при фиксированной длине кодового слова уменьшает число информационных символов, а следовательно и скорость передачи информации.
– скорость передачи информации
k – число информационных символов
n- длина кода
Т.о. хорошие корректирующие свойства кода и высокая скорость передачи информации – противоречивые требования. Поэтому задача построения кода с приемлемыми значениями (d,R) задача оптимизации, не имеющая единственного решения. Параметры (n,k,d) не могут принимать произвольные значения, так:
1. среди кодов с одинаковыми n и k лучшим является код, который имеет большее кодовое расстояние d.
2. Среди кодов с одинаковыми n и d лучшим является код, который имеет большее число информационных символов k.
3. Среди кодов с одинаковыми k и d лучшим является код, который имеет меньшую длину n, а следовательно и меньшее число проверочных символов.
Т.о. между n, k и d существуют определенные соотношения, задаваемые границами для кодового расстояния или для скорости передачи информации. Различают верхние и нижние границы.
Верхняя граница Хэмминга
Теорема: «Верхняя граница Хемминга»
Если
существует линейный q-ый
код длиной блока n,
k
информационными символами и d=2t+1,
где t-число
ошибок, то
.
Пример:
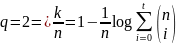
Равенство
достигается, когда
,
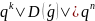где
-
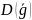число кодовых слов.
Коды, для которых выполняется равенство, называются совершенными или плотно упакованными. Примером такого кода является код кратных повторений.
Верхняя граница Плоткина
Теорема: «Верхняя граница Плоткина»
Если
существует q-ый
код длиной блока n
с общим числом кодовых слов M
и кодовым расстоянием D,
то выполняется
.
Коды, для которых выполняется равенство, называются эквидистантными. Это означает, что если для кода выполняется равенство, то расстояние между двумя любыми кодовыми словами одинаково. Примером такого кода является код кратных повторений.
Пример:
изображается в трехмерной системе
координат в виде куба. Этот код называется
симплексным.
Пример: все коды, построенные с использованием матрицы Адамара.
Нижняя граница Варшамова-Гилберта.
Теорема: «Нижняя граница Варшамова-Гилберта»
Существует
код с кодовым расстоянием равным поменьше
мере t,
параметры которого удовлетворяют
неравенству
.
Для оценки границ кода используются оценки Чернова.
Теореме:
Пусть
число
,
тогда справедливы оценки
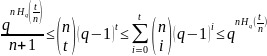
При больших n имеются асимптотическое предстваление границ Хемминга, Плоткина, Варшамова-Гилберта:
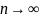
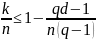
Рассмотренные оценки применяются и для нелинейных блоковых кодов.
Графическое представление оценок:
График…
Характеристика графика: при малой скорости и передаче более точной верхней границей является граница Плоткина, при большей – граница Хемминга. При больших значения n, наилучшей верхней границей считается Мак-Элиса-Родемича-Рамсея-Велча. Область значения параметров, для которых могут существовать коды, отмечена штрихом.
Стандартное расположение векторов векторного пространства.