
- •Понятие дискретного источника сообщений.
- •Первая и вторая теорема Шеннона для источников без памяти
- •Оптимальное кодирование. Основные понятия и определения.
- •Однозначная декодируемость неравномерного кода.
- •Методы построения префиксных кодов. Метод Шеннона.
- •Свойства оптимального кода.
- •Алгоритм Хаффмана.
- •Блоковые коды
- •Линейные коды.
- •Эквивалентные и систематические коды.
- •Стандартное расположение.
- •Декодирование с использованием синдромов.
- •Последовательное декодирвание.
- •Методы построения новых кодов. Методы: добавление общей проверки на четность; выкалывание кодовых координат.
- •Определения
Понятие дискретного источника сообщений.
Под ДИС понимают устройство, порождающее последовательности, составленные из букв конечного алфавита А, мощностью n<∞. При этом буквы последовательности порождаются в дискретные моменты времени.
t = 0, 1, 2, …
t = …, -2, -1, 0, 1, 2, …
Введение этих условий (конечность, дискретные моменты времени) обуславливает название этих источников. Всякий непрерывный источник информации можно в некотором смысле заменять с заданной степенью точности некоторым дискретным источником.
Последовательности, порождаемые ДИ можно рассматривать как траектории некоторых случайных процессов, задание которых и позволит ввести математическую модель источника.
Пусть бесконечная в обе стороны последовательность букв
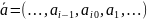
представляет
собой некоторую возможную реализацию
источника. Будем рассматривать
последовательность
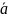 как элементарное событие некоторой
σ-алгебры, задание которой, вместе с
вероятностной мерой P
даёт основание интерпретировать
как некоторую траекторию случайного
процесса.
как элементарное событие некоторой
σ-алгебры, задание которой, вместе с
вероятностной мерой P
даёт основание интерпретировать
как некоторую траекторию случайного
процесса.
Совокупность
таких элементарных событий обозначим
A
= { .
Любое подмножество множества AI
представляет некоторое событие σ-алгебры.
Введём в рассмотрение событие следующего
вида:
.
Любое подмножество множества AI
представляет некоторое событие σ-алгебры.
Введём в рассмотрение событие следующего
вида:
Пусть в момент времени t1 источник порождает букву ai1ϵ A. Тогда это событие Ct1(ai1) является объединением всех таких элементарных событий , в которых координата с номером t в последовательности не фиксированы:

где xt – произвольные буквы алфавита A и t≠ti.
Если t1, .., tm – любые целые числа; ai1, …, aim – буквы из алфавита А, то событие Ct1…Ctm(ai1, …, aim) = {источник порождает букву aix в момент времени tk, где 1≤k≤m} – множество всех последовательностей , у которых определённая координата, соответствующая моменту времени tk фиксирована: xtk = aik, k=1, …, m. Остальные координаты не фиксированы и могут принимать произвольные значения из A.
Математическое описание дискретного источника сообщений.
Цилиндрическим множеством (цилиндром) называется случайное событие Ct1…Ctm(ai1, …, aim).
Математическое описание источника задаётся как описание некоторого случайного процесса и состоит в задании:
Некоторого конечного алфавита A
σ-алгебры элементарных событий
вероятностной меры
Для ДИС вводят следующие обозначение: [A, P(s)], P(AI)=1.
Пусть ϵ AI. Тогда через T обозначим последовательность
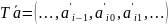
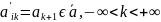
T представляет собой сдвиг на один шаг влево исходной последовательности .
Если RcAI, то TR – совокупность всех T , для которых ϵR, т.е. ϵR T ϵTR. Очевидно, что TAI = AI.
Понятие стационарного источника
Пусть
А — {a1,...,ak.}
— конечный алфавит и х ϵ А∞. Будем
обозначать через
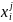 подслово последовательности x,
начиная с i-й
и заканчивая j-й буквой, а через xn
начало последовательности x
длины n,
т. е.
подслово последовательности x,
начиная с i-й
и заканчивая j-й буквой, а через xn
начало последовательности x
длины n,
т. е.
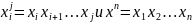 .
Дискретным источником X называется
дискретный случайный процесс со
значениями в А. Источник полностью
задается вероятностями Pr(Xn=xn),
которые определены для всех xn
ϵ An
и целых n>0
и удовлетворяют равенствам
.
Дискретным источником X называется
дискретный случайный процесс со
значениями в А. Источник полностью
задается вероятностями Pr(Xn=xn),
которые определены для всех xn
ϵ An
и целых n>0
и удовлетворяют равенствам
 .
Тогда
.
Тогда
 .
Источник X
называется стационарным, если для всех
целых t>0
и
.
Источник X
называется стационарным, если для всех
целых t>0
и
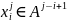 справедливы равенства
справедливы равенства
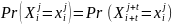 .
.
Энтропия стационарного источника
Введем
обозначение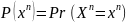 .
Для каждого стационарного
.
Для каждого стационарного
источника
X равенство
 определяет неотрицательную величину
Н(Х), которая называется энтропией
источника.
определяет неотрицательную величину
Н(Х), которая называется энтропией
источника.
