
- •Дайте определение скалярного произведения в Rn. Приведите неравенство Коши-Буняковского и проиллюстрируйте его на примере.
- •Дайте определения вырожденной и невырожденной квадратных матриц порядка 3. Приведите примеры таких матриц. Докажите, что ортогональная матрица является невырожденной
- •Выведите канонические уравнения прямой в r3, проходящей через данные точки и .
- •Дайте определение скалярного произведения в пространстве . Дайте определение евклидова пространства. Сформулируйте неравенство Коши-Буняковского и проиллюстрируйте его на примере.
- •Сформулируйте теорему двойственности и привести пример
- •Может ли квадратное уравнение в области комплексных чисел: а) не иметь корней; б) иметь ровно один корень; в) иметь два корня; г) иметь более двух корней? Решите уравнение .
- •Найдите угол между плоскостями , . Найдите угол между прямой и плоскостью в ?
- •Сформулируйте правило Крамера для решения систем линейных уравнений. Докажите правило Крамера для системы линейных уравнений от двух переменных.
- •Какие уравнения окружности, эллипса и гиперболы называется каноническими? Какая из линий второго порядка обладает асимптотами? Напишите каноническое уравнение этой линии и уравнения ее асимптот.
- •Дайте определение скалярного произведения в пространстве . Приведите неравенство Коши-Буняковского и проиллюстрируйте его на примере.
- •Дайте определения стандартной и канонической задач линейного программирования. Приведите к стандартной и канонической формам следующую задачу
- •Выведите уравнение прямой в , проходящей через данную точку в данном направлении .
- •Дайте определение линейного пространства. Приведите примеры линейных пространств, отличных от арифметических пространств .
- •Как найти угол между прямой и плоскостью в ? Ответ обоснуйте и приведите пример.
- •3.Дайте определение отрезка, луча. Напишите задающее их ур-ние и неравенство в r3. Как проверить, лежит ли точка на заданном отрезке? Приведите примеры.
- •Дайте определение аргумента комплексного числа и укажите способ его нахождения. Найдите аргумент числа . Какой аргумент имеет число ?
- •Образует ли линейное пространство множество квадратных матриц порядка , удовлетворяющих условию ? Ответ обосновать. Найдите размерность этого пространства.
- •2. Сформулируйте правило Крамера для решения систем линейных уравнений. Приведите пример применения правила Крамера для системы линейных уравнений от трех переменных.
- •Билет 19
- •1) Сформулируйте закон инерции квадратичных форм. Можно ли квадратичную форму с помощью невырожденного линейного преобразования переменных привести к виду ? Ответ обоснуйте.
- •2) Как определяется операция умножения матрицы а на число ? Приведите пример. Как связаны определители квадратных матриц а и размера nxn? Ответ обоснуйте.
Может ли квадратное уравнение в области комплексных чисел: а) не иметь корней; б) иметь ровно один корень; в) иметь два корня; г) иметь более двух корней? Решите уравнение .
Теорема: всякий многочлен с любыми числовыми коэффициентами, степень которых не меньше 1, имеет хотя бы один корень, в общем случае комплексный (т. е. другими словами всегда имеет n корней).
Может иметь только 2 корня, так как остальные варианты противоречат основной теореме алгебры. (в)
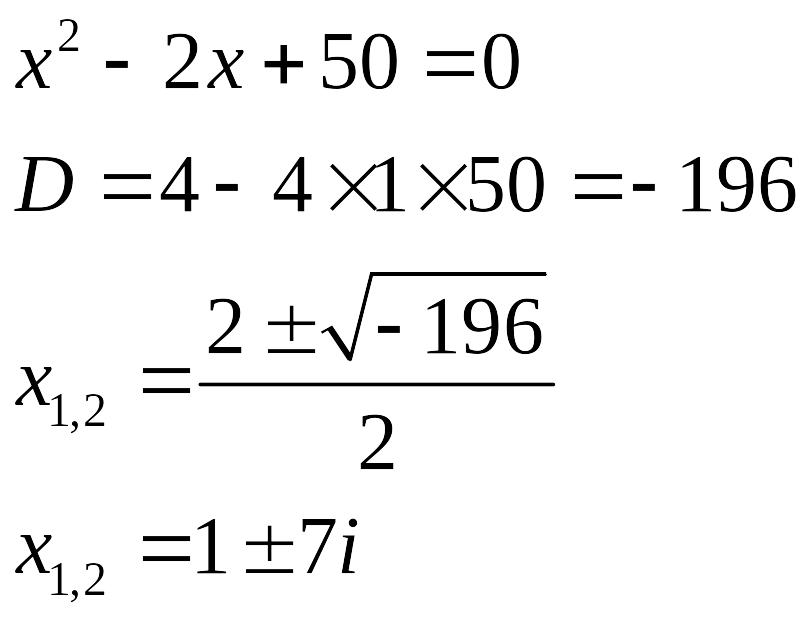
Укажите, какие из равенств не выполняются для любых матриц
 ,
,
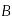 ,
,
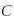 (предполагается, что все произведения
определены): а)
(предполагается, что все произведения
определены): а)
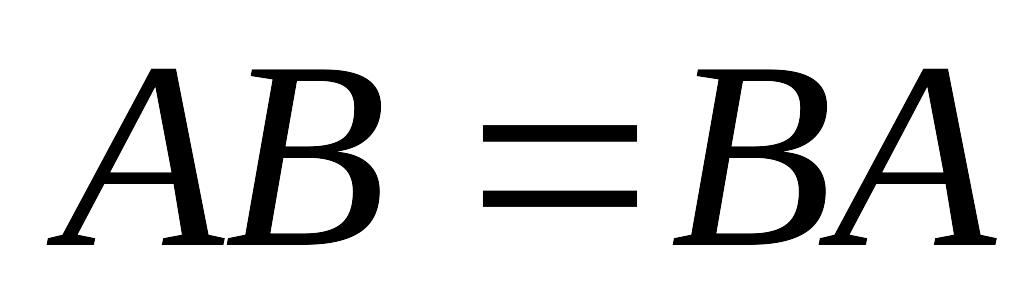 ; б)
; б)
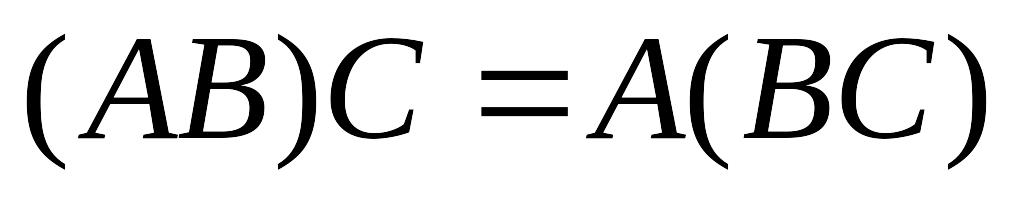 ; в)
; в)
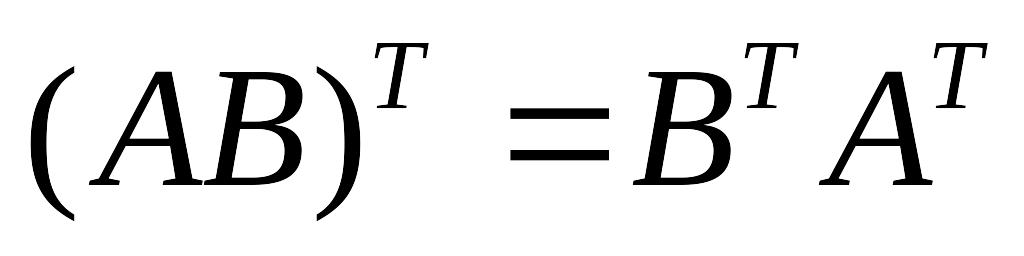 ; г)
; г)
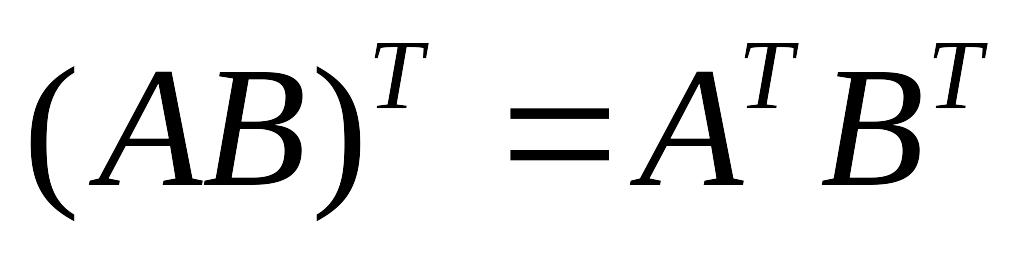 .
Приведите примеры, опровергающие
неверные равенства.
.
Приведите примеры, опровергающие
неверные равенства.
Определение: Матрица – прямоугольная таблица чисел. Отдельные числа (или символы, их заменяющие) называют элементами матрицы.
a11 a12 …a1n
a21 a22 …a2n
…
an1 an2 …ann
mxn – порядок матрицы.
Свойства сложения.
1.Ассоциативность:А+(В+С)=(А+В)+С
2. Коммутативность: А+В=В+А.
3. А+0=А.
Разность матриц: А-В = А+(-1)В
Свойства умножения матриц:
Если матрицы А, В и С таковы, что их произведение возможно, то
1. (АВ)С = А(ВС)
2. А(В+С)=АВ+АС
3. (В+С)А=ВА+СА
4.
![]()
5.
![]() – умножение матриц не обладает свойством
коммутативности.
– умножение матриц не обладает свойством
коммутативности.
Не выполняется АВ=ВА, пример: А – матрица порядка 2х2, В порядка 2х3, в этом случае АВ не равняется ВА, т.к. ВА не существует.
A
=
![]() , B
=
, B
=
![]() ,
,
то
AB
=
, а BA
=
![]()
Не выполняется АВт = Ат *Вт, пример: А – матрица порядка 2х2, а В порядка 2х3, в этом случае АВт не равняется Ат*Вт, т.к. Ат*Вт не существует.
Остальные равенства выполняются для любых матриц АВС.
Найдите угол между плоскостями , . Найдите угол между прямой и плоскостью в ?
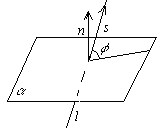
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
![]()
Рассмотрим
векторы
![]() и
и
![]() .
Если угол между ними острый, то он будет
.
Если угол между ними острый, то он будет
![]() ,
где φ – угол между прямой и плоскостью.
Тогда
,
где φ – угол между прямой и плоскостью.
Тогда
![]() .
.
Если
угол между векторами
![]() и
тупой,
то он равен
и
тупой,
то он равен
![]() .
Следовательно
.
Следовательно
![]() .
Поэтому в любом случае
.
Поэтому в любом случае
![]() .
Вспомнив формулу вычисления косинуса
угла между в
.
Вспомнив формулу вычисления косинуса
угла между в екторами,
получим
екторами,
получим
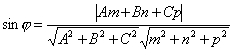
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
![]()
Под
углом
между двумя плоскостями будем понимать
один из двугранных углов, образованных
этими плоскостями. Очевидно, что угол
между нормальными векторами
![]() и
и
![]() плоскостей
α1
и α2
равен одному из указанных смежных
двугранных углов
плоскостей
α1
и α2
равен одному из указанных смежных
двугранных углов
![]() или
или
![]() .
Поэтому
.
Поэтому
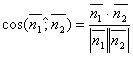 .
Т.к.
.
Т.к.![]() и
и
![]() ,
то
,
то
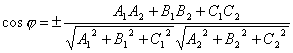 .
.
№8
z=-2x1-3x4![]() max
max
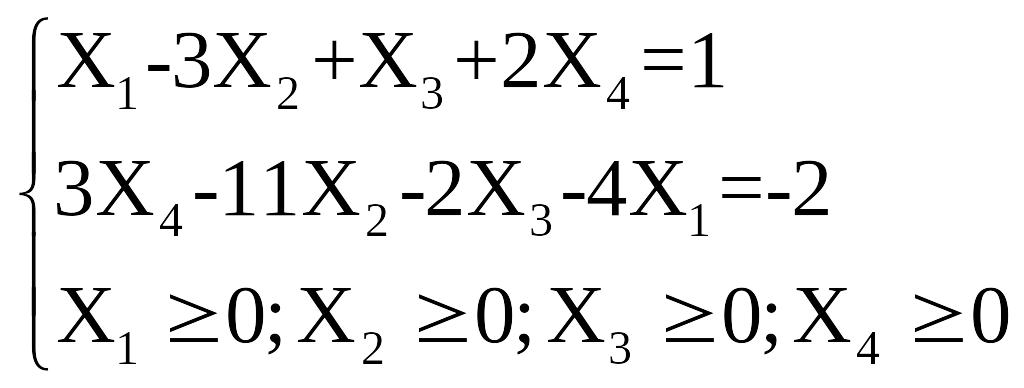
1 3 1 2 1
-4 -11 -2 3 -2

1 3 1 2 1
0 1 2 11 2
1 0 -5 -11 -5
0 1 2 11 2
1 2 11 2
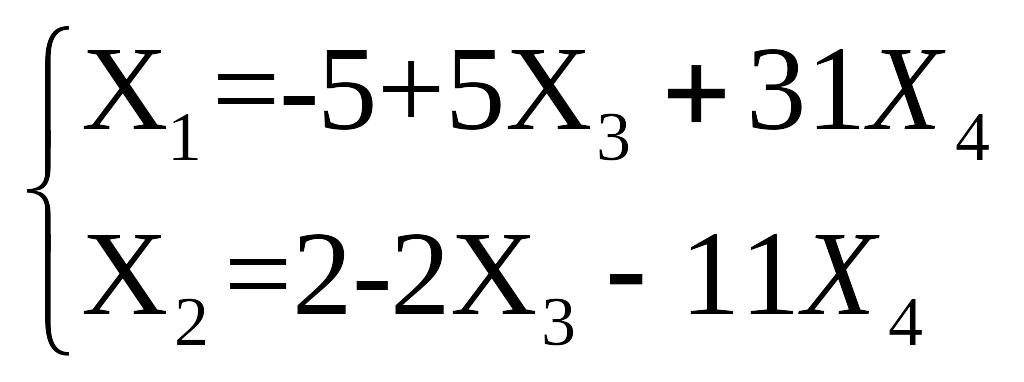
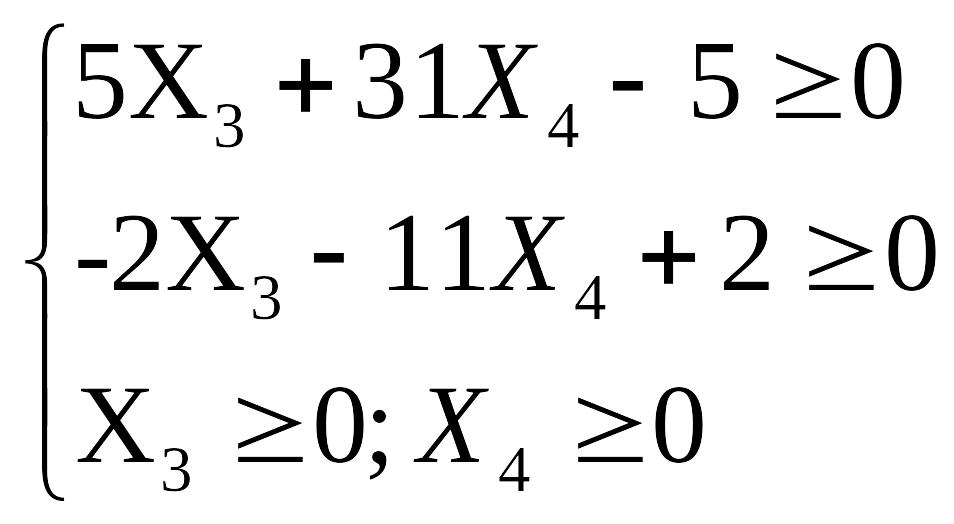
Z=10-10X3-62X4-3X4=10-10X3-65X4
В 07
1)
Дaйте
определение ортонормированной системы
векторов. Приведите пример ортонормированной
системы в
![]() .
Докажите, что ортонормированная система
в
,
состоящая из трех векторов, является
базисом пространства
.
.
Докажите, что ортонормированная система
в
,
состоящая из трех векторов, является
базисом пространства
.
Система векторов e1, e2, …, en евклидова пространства называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину. Пример: a1=(0,1), a2=(1,0)
В
ортонормиров. сист. векторы ортогональны
по определению. Докажем, что они ЛНЗ.
Предположим противное, тогда
![]() ,
где не все «лямбда» равны 0. Пусть
,
где не все «лямбда» равны 0. Пусть
![]() Умножим рав-во по правилу скалярного
произв-ия на а1.
Т.к. векторы взаимно ортогональны, т.е.
(ai,aj)=0
и т.к. (0,а1)=0,
мы получим:
Умножим рав-во по правилу скалярного
произв-ия на а1.
Т.к. векторы взаимно ортогональны, т.е.
(ai,aj)=0
и т.к. (0,а1)=0,
мы получим:
![]() ,
то (a1,a1)=0,
и, следовательно, a1=0,
что противоречит условию (векторы
ненулевые).
,
то (a1,a1)=0,
и, следовательно, a1=0,
что противоречит условию (векторы
ненулевые).
Итак, 3 вектора пространства ЛНЗ, следовательно, они являются базисом.
