5. Дайте определение скалярного произведения в пространстве . Дайте определение евклидова пространства. Сформулируйте неравенство Коши-Буняковского и проиллюстрируйте его на примере.

Скалярным произведением двух векторов a=(a₁ , a₂ , ..., a_n ) и b=(b₁, b₂, ..., b_n) называется число (a, b)=a₁b₁+a₂b₂+ ...+a_nb_n.

Основные свойства скалярного произведения векторов: 1.)=(b, a). 2. (ka, b)=k (a, b) 3. (a, b+ c)=(a, b)+ (a, c) 4. (a, a)> 0, если а= 0 и (a, a)= 0, если a=0

cos.=(a, b)/ |вектор а|*|вектор в|

Равенство справедливо при векторе а0 и векторе в0. Однако формула не совсем проста. Уравнение cos = с, (где  - неизвестное число) имеет решение только при –1c1. Поэтому, чтобы данное нами определение угла между векторами было корректным, необходимо сначала убедиться, что (a, b)/ |вектор а|*|вектор в| заключено между -1 и 1. Для этого имеется Неравенство Коши-Буняковского. Для любых двух векторов a и b из Rⁿ справедливо неравенство (a,b)²<(a,a)* (b,b).

Линейное пространство называется евклидовым, если каждой паре векторов , из этого пространства поставлено в соответствие действительное число , называемое скалярным произведением, и при этом для любых из и любого действительного числа справедливы следующие равенства:

1. ;

2. ;

3. ;

4. при , ,   -- нулевой вектор.

3. Сформулируйте теорему двойственности и привести пример

Первая теорема:

Если одна из двойственных задач имеет оптимальное решение, то и другая задача также имеет оптимальное решение, причем максимум (минимум) целевой функции одной из этих задач численно равен минимуму (максимуму) целевой функции другой задачи.

Вторая теорема:

Если оптимальному решению одной из двойственных задач соответствует нестрогое неравенство в i-том ограничении этой задачи, то соответствующая переменная в оптимальном решении двойственной задачи равна нулю.

№ 4.

Проверка:

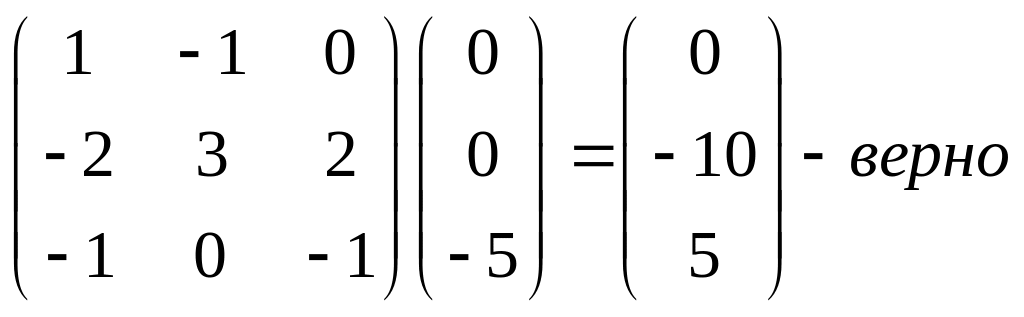
№5

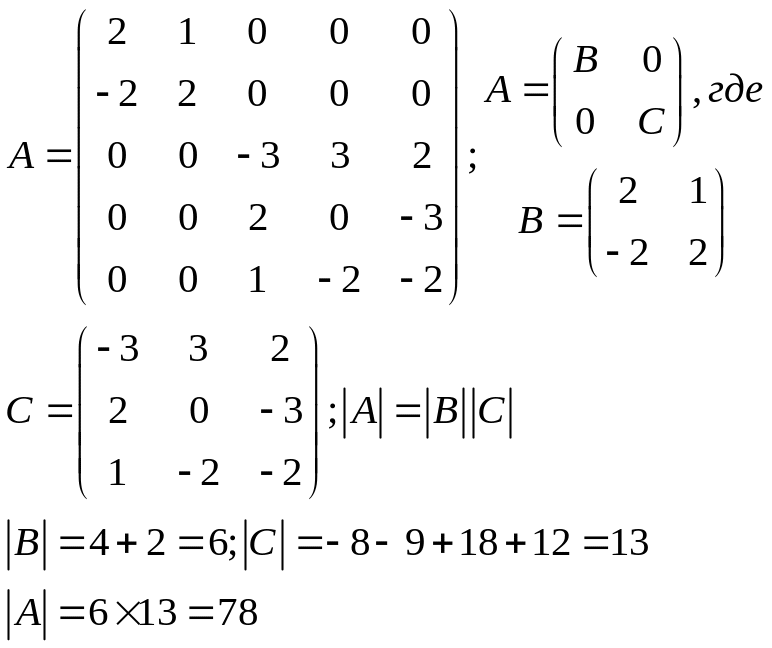
Ответ: 78.

7 . Найти общее уравнение плоскости, содержащей прямую и параллельной ей прямой .

Поскольку , положим точку начальной точкой плоскости , а направляющий для вектор -одним из направляющих векторов плоскости направляющий для прямой . Тогда уравнение плоскости запишем в виде:

6. Найти собственные значения матрицы , если

; =44+12=56

;

Задание 5

Дана матрица

=А

А= В 0

0 С

Определитель А = ОпределительВ * ОпределительС

ОпределительВ = 4+2=6

ОпределительС=-8-9+18+12=13

ОпределительА=6*13=78

Ответ:78

Задание 6.

С^-1 – собств. Значен., если

С= 11 6

-2 4

Собств. Значения С^-1 равны лямбда^-1, где лямбда – собствен значения С – следовательно ищем собственные значения С

С-лямбдаЕ= 11-лямбда 6

-2 4-лямбда

Определитель (С-лямбдаЕ) = 0

Значит, (11-Л)(4-Л)+12=0

Л²-15Л+56=0

Л1=7 Л2=8

Значит, Л1(для С^-1 )= 1/7

Л2=1/8

В 04

6. Сформулируйте основную теорему алгебры. Решите уравнение x³+27 = 0 .

Основная теорема алгебры – теорема о комплексных числах. Комплексное число Z = a + ib, где a и b – действительные числа; слагаемые a и b называются соответственно действительной и мнимой частью комплексного числа; символ i, определяемый условием i² = -1, называется мнимой единицей. Комплексные числа вводятся в связи с необходимостью решать уравнения вида X² + 1 = 0.

Теорема: всякий многочлен с любыми числовыми коэффициентами, степень которых не меньше 1, имеет хотя бы один корень, в общем случае комплексный (т. е. другими словами всегда имеет n корней).

7. Пусть , ..., - векторы из R⁶. Можно ли составить базис пространства R⁶ из линейных комбинаций этих векторов? Ответ обоснуйте. Докажите, что три вектора пространства линейно зависимы.

Нет нельзя т.к. это противоречит теореме о том, что линейно независимая система векторов в тогда и только тогда является базисом, когда число этих векторов равно n.

8. Напишите каноническое уравнение окружности. При каком значении параметра , уравнение определяет окружность?

(x-x₀)² + (y-y₀)² = R²

x² + y² + 2x - 4y + p = 0

(x² +2x + 1) - 1 +(y² - 4y + 4) - 4 + p = 0

(x+1)² + (y-2)² = -p +5

5-p >= 0

p <= 0

№5.

Появилась закономерность =>

№6

Где

№7.

№8

- точка минимума

, точка минимума .

В 05

9. Дайте определение числа, сопряженного к данному комплексному числу . Приведите пример. Покажите, что для комплексных чисел , : a) , б) .

Комплексное число a - ib называется сопряженным с числом z = a + ib и обозначается .

10. Дайте определение произведения матриц и . Приведите пример, когда существует, а - нет. Существуют ли ненулевые квадратные матрицы и такие, что ? Существуют ли матрицы и такие, что , а . Ответы обоснуйте.

Пусть даны матрицы и .

* =

Получаем матрицу С, каждый элемент которой равен сумме произведений элементов i–ой строки А на соотв. элемент j–го столбца В.

1) Произведением матрицы A = ( ) размера m n на матрицу B = ( ) размера n s называется матрица AB = ( ) размера m s элементы которой определяются формулой:

2) Да существует, например и

3) Нет, не существует т.к. это противоречит основному свойству определителей:

det(AB) = detAdetB

AB=0 detA+detB = 0

BA=E detBdetA = 1

11. Дайте определение гиперболы. Каков геометрический смысл параметров, входящих в каноническое уравнение гиперболы? Среди линий , , выберите гиперболы и постройте схематично их графики.

Гипербола – геометрическое место точек модуль разности расстояний от которых до двух заданных точек(фокусов) постоянен. ׀v₁-v₂׀=2a/

x²/a² - y²/b²=1 – каноническое ур-ие гиперболы.

b²=c²-a^2.

E=c/a E>1.

y=(±b/a)x. r=p/(1+Ecosφ) – полярное ур-ие.

Прямые L1 и L2, уравнения которых у=+- (b/a)х называются асимптотами гиперболы, где а и b действительные мнимые полуоси гиперболы.

№5.

№6

A=

По критерию Сильвестра:

D₁=

D₃

=> да, яв-тся

№7 А(6;6) l

l -?

x-6= -y+6

x+y-12=0 – общий вид - Ур-е в отрезках.

- параметрический вид

В 06