В 01
Дайте определение скалярного произведения в Rn. Приведите неравенство Коши-Буняковского и проиллюстрируйте его на примере.
Скалярным произведением двух векторов a=(a1 , a2 , ..., an ) и b=(b1, b2, ..., bn) называется число
Основные свойства скалярного произведения векторов:
(a,b)=(b, a).
(ka, b)=k (a, b)
(a, b+ c)=(a, b)+ (a, c)
(a, a)> 0, если а= 0 и (a, a)= 0, если a=0
cos.=(a, b)/ |вектор а|*|вектор в|
Равенство справедливо при векторе а0 и векторе в0. Однако формула не совсем проста. Уравнение cos = с, (где - неизвестное число) имеет решение только при –1c1. Поэтому, чтобы данное нами определение угла между векторами было корректным, необходимо сначала убедиться, что (a, b)/ |вектор а|*|вектор в| заключено между -1 и 1. Для этого имеется Неравенство Коши-Буняковского. Для любых двух векторов a и b из Rn справедливо неравенство (a,b)2<(a,a)* (b,b).
Дайте определения вырожденной и невырожденной квадратных матриц порядка 3. Приведите примеры таких матриц. Докажите, что ортогональная матрица является невырожденной
Матрица А порядка n*n называется невырожденной, если ее строки линейно независимы, в противном случае – вырожденная.
Теорема: квадратная матрица А невырождена тогда и только тогда, когда ее определитель |А| не равен нулю.
|А|
=
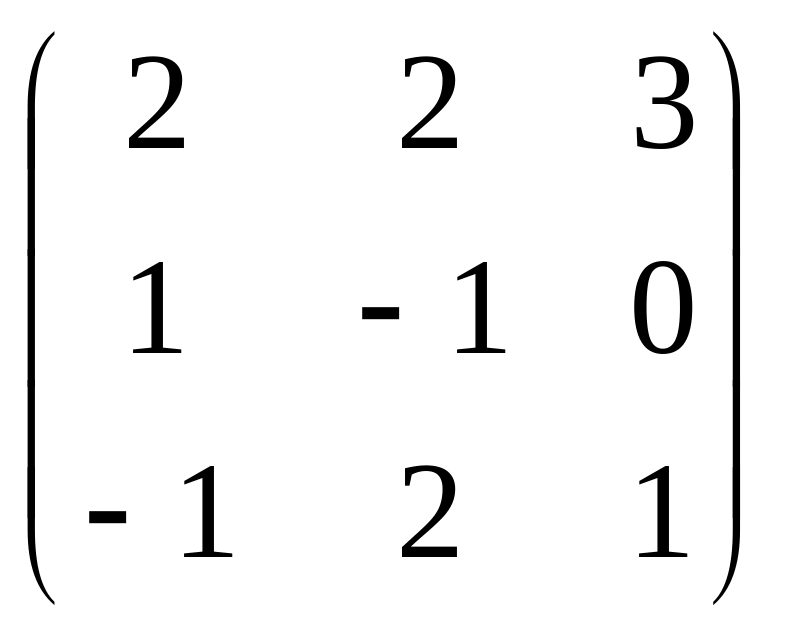= -1
0 – невырожд.
Квадратная матрица A называется ортогональной, если соответствующая ей система векторов столбцов является ортонормированной.
(ai,aj)=∑k=1nakiakj= δij
Пусть A - ортогональная матрица.
AT=A-1 –необходимое и достаточное условие ортогональности матрицы A.
ATA=E (по определению), A-1A=E.
А т.к. обратная матрица существует, если А невырожденная, то ортогональная матрица является невырожденной.
Выведите канонические уравнения прямой в r3, проходящей через данные точки и .
Положим начальной точкой, вектор = (b1-a1, b2-a2, b3-a3) - направляющим вектором, тогда каноническое Ур-е прямой, проходящей через точки А и В, примет вид:
Билет 2
1) В пространстве Rn существует ортонормированный базис, состоящий из собственных векторов симметрического линейного преобразования, в котором матрица имеет диагональный вид.
Векторы базиса ЛНЗ векторы, кол-во которых равно n.
Симметр. матрица порядка 3 может иметь максимум 3 ЛНЗ собств. вектора.
№ 4
Пишем уравнение.
Процесс преобразования закончен. Получилась система уравнений с базисными неизвестными x1, x2, x3 и свободным неизвестным x4. Наличие свободного неизвестного означает, что решений – бесконечное множество. Значит, система векторов линейно зависима.
№5.
Запишем определитель матрицы:
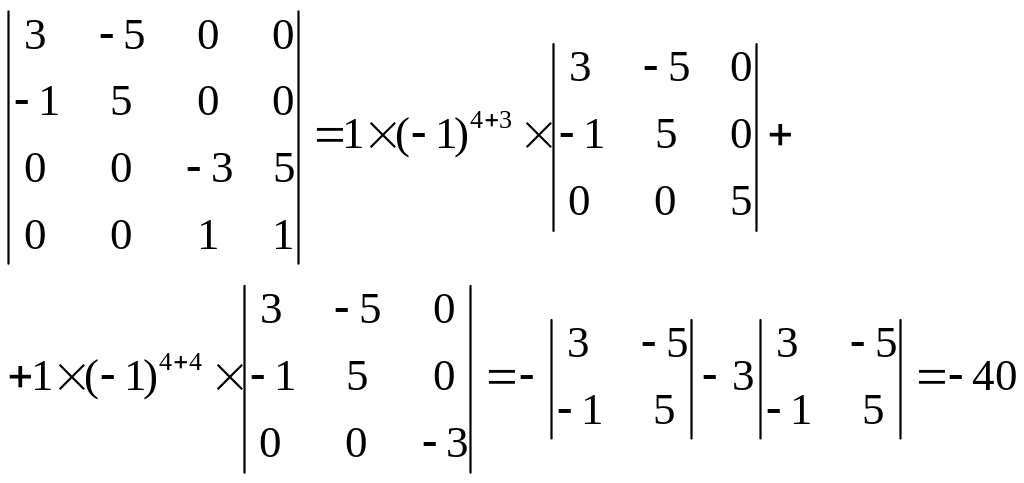
Ответ:-40.
№6
Найдём
собственные значения матрицы С4,
если
Найдём собственные значения матрицы С:
Тогда собственные значения матрицы С4 равны:
Ответ:
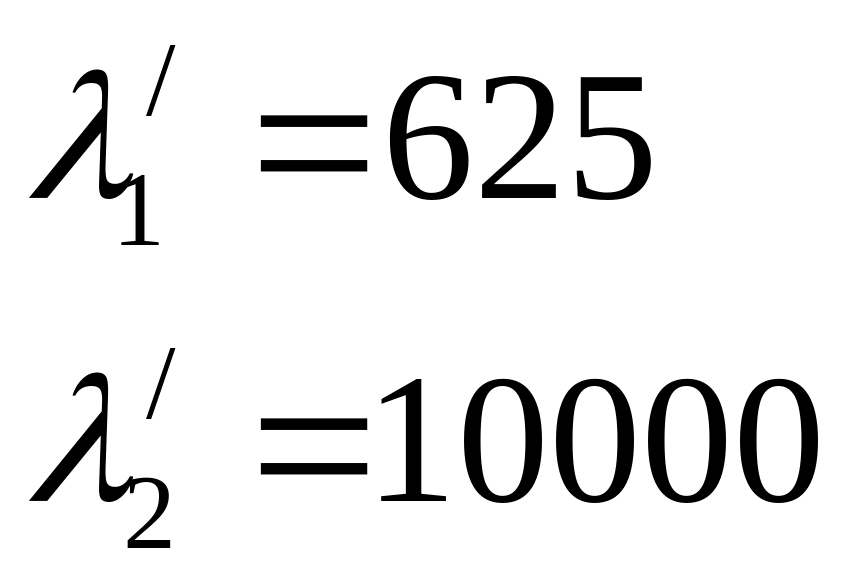
№7
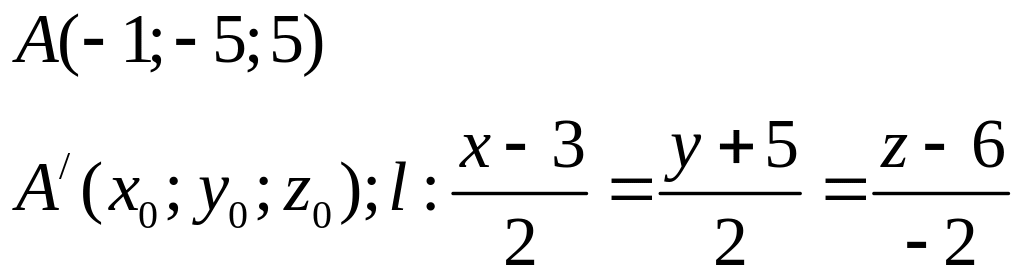
П:
Запишем
параметр. ур-е прямой
с начальной точкой
и направл. вектором
.
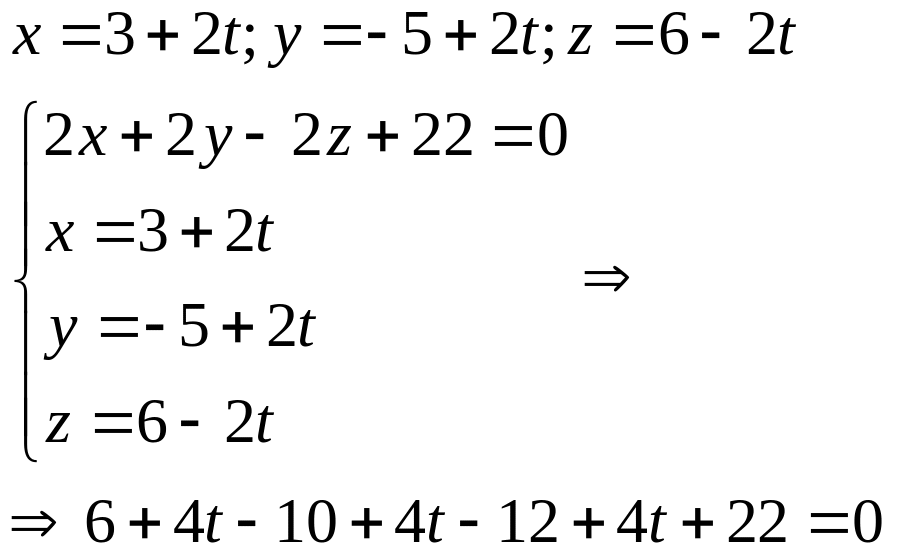
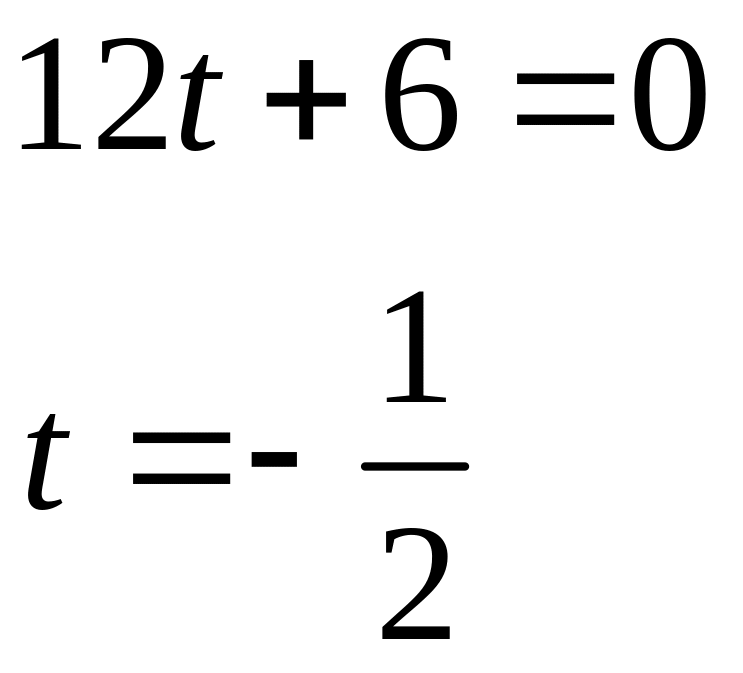
Тогда
x=3-1=2;
y=-6;
z=7.
Итак, получим
.
Найдём
:
Ответ:
В 03
Дайте определение матрицы линейного оператора в данном базисе. Приведите пример. Как изменяется матрица линейного оператора при переходе от одного базиса к другому? Ответ проиллюстрируйте на примере.
Выберем в пространстве L базис e1, e2 …, en. x=x1e1+x2e2+…+xnen - разложение произвольного эл-та x по данному базису. y=Ấ(x). В силу линейности оператора Ấ получаем y=Ấ(x) =x1Ấ(e1)+…+xnẤ(en).
Поскольку Ấ(ei) также эл. из L, то его можно разложить по этому базису. Ấ(ei)=a1ie1+a2ie2+…+anien ( i=1,2,3…n). Тогда Ấ(x)=x1(a11e1+a21e2+…an1en)+ x2(a12e1+a22e2+…+an2en)+…+xn(a1ne1+a2ne2+…+amnen)=(a11x1+a12x2+ +…+a1nxn)e1+(a21x1+a22x2+…+a2nxn)e2+…+(an1x1+an2x2+…+annxn)en. С другой стороны эл. y=Ấ(x) можно разложить в данном базисе
y=Ấ(x)=y1e1+y2e2+…+ynen. Ввиду единственности разложения вектора по базису:
y1=a11x1+a12x2+…+a1nxn
y2=a21x1+a22x2+…+a2nxn
. . . . . . . . . . . . . . . . . .
yn=an1x1+an2x2+…+annxn
y=x1A1+…+xnAn. Ai=Ấ(ei) - столбец. Ae=(A1… An)
Матрица Ae=(aije) (i,j = 1,2,..,n) называется матрицей оператора Ấ в базисе e1, e2,… en. Таким образом каждому линейному оператору соотв. матрица в данном базисе. Связь между эл. x и его образом y, равному Ấ(x), можно выразить в матричной форме уравнением: Y=AX. X=(x1, x2,…, xn)T