
- •Оглавление
- •ГЛАВА 1 РАСЧЕТ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
- •Тема 1 Метод эквивалентных преобразований
- •Тема 2 Метод напряжения между двумя узлами
- •Тема 3 Метод эквивалентного генератора
- •ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
- •Тема 1 Расчет действующих значений токов и напряжений
- •Тема 2 Символический метод расчета
- •Тема 3 Анализ резонансных режимов
- •Тема 4 Анализ цепей с взаимной индуктивностью
- •ГЛАВА 3 РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ
- •Тема 1 Расчет цепей с симметричной системой ЭДС
- •Тема 2 Расчет цепей с несимметричной системой ЭДС
- •Тема 1 Однофазные цепи несинусоидального тока
- •Тема 2 Высшие гармоники в трехфазных цепях
- •ГЛАВА 5 ПЕРЕХОДНЫЕ ПРОЦЕССЫ
- •ГЛАВА 7 МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
- •ГЛАВА 8 НЕЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- •ГЛАВА 9 ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
- •ЗАКЛЮЧЕНИЕ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 2 Символический метод расчета
|
R |
* |
|
|
* W |
U |
XC |
A |
|
||
|
|
|
|
R1 |
X L |
Рис. 2.34
Ответ: PW = −5 Вт.
Тема3 Анализ резонансных режимов
Резонансные режимы могут быть в цепях, содержащих индуктивные катушки и конденсаторы, которые компенсируют действие друг друга.
Занятие1
Цели занятия:
1.Научиться строить векторные диаграммы при резонансе напряжений.
2.Научиться использовать условие резонанса для расчета цепей с последовательным соединением приемников.
Если в условии заданы токи и напряжения, для решения задачи нужно построить векторную диаграмму. Алгоритм ее построения не отличается от рассмотренных ранее, но векторы входного тока и входного напряжения при резонансе направлены одинаково.
Если в условии задачи заданы параметры схемы (R, L, C), для решения необходимо использовать условие резонанса. При резонансе напряжений
вцепи с последовательным соединением приемников входное реактивное сопротивление Х = 0. В целом цепь имеет чисто активный характер. Ток на входе цепи совпадает по фазе с входным напряжением (ϕ = 0), поэтому
потребляемая мощность Р = U I .
Рассмотрим алгоритмы решения целевых задач на конкретных примерах.
Теоретические основы электротехники. Практикум |
-83- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
Задача1
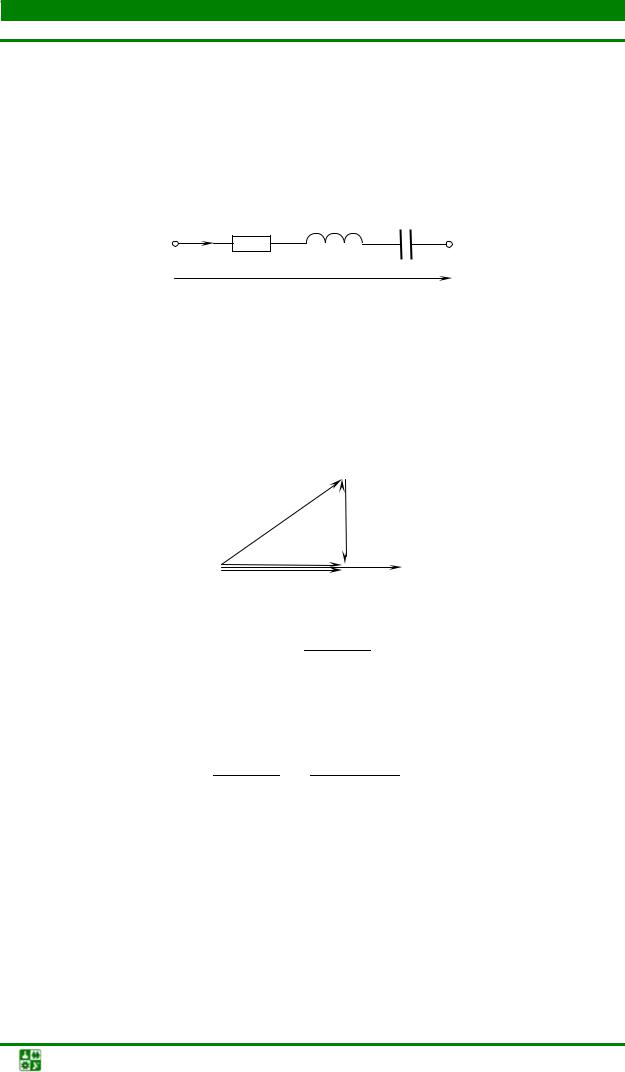
На рис. 2.35 изображена схема замещения цепи с последовательным соединением реальной индуктивной катушки и конденсатора. Вычислить напряжение на реальной катушке, если в резонансном режиме U =120 В,
UC =160 В.
I |
R |
X L |
XC |
|
|
||
|
|
U |
|
Рис. 2.35
Решение
1. В условии задачи заданы электрические величины, поэтому для решения нужно построить векторную диаграмму (рис. 2.36). Алгоритм построения диаграммы подробно изложен в занятии 1 темы 1. Напряжение на реальной индуктивной катушке
UK |
|
UC |
UR |
UL |
|
|
|
I |
U
Рис. 2.36
UK = 
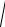 UR2 +UL2 .
UR2 +UL2 .
При резонансе напряжений U L =UC , U R =U . Поэтому
UK = 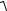
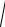 U 2 +UC2 =
U 2 +UC2 = 
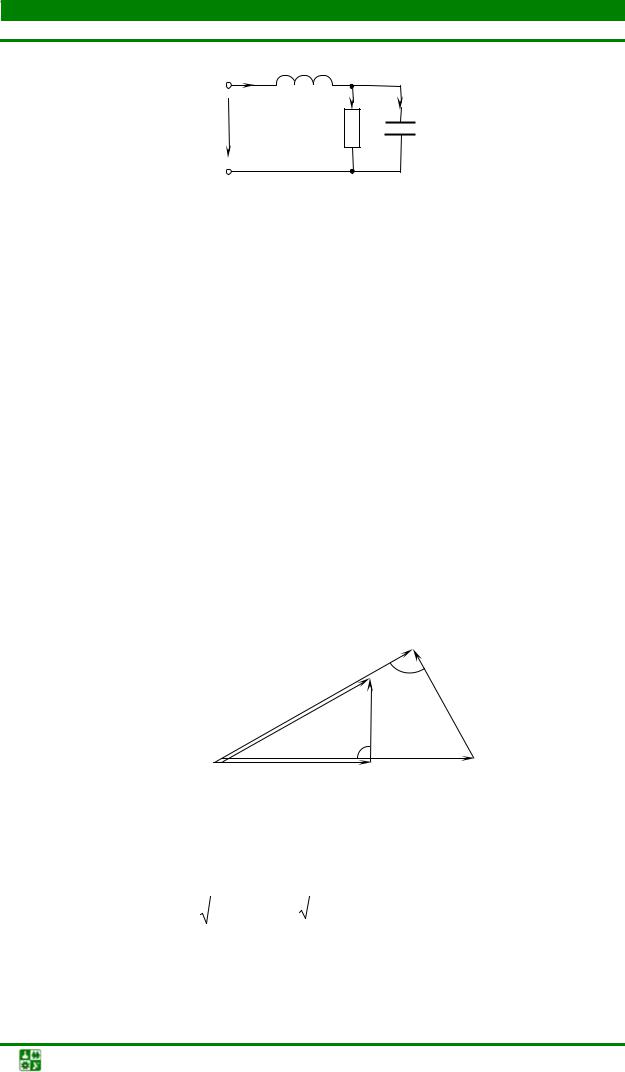
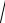 1202 +1602 = 200 В.
1202 +1602 = 200 В.
Задача2
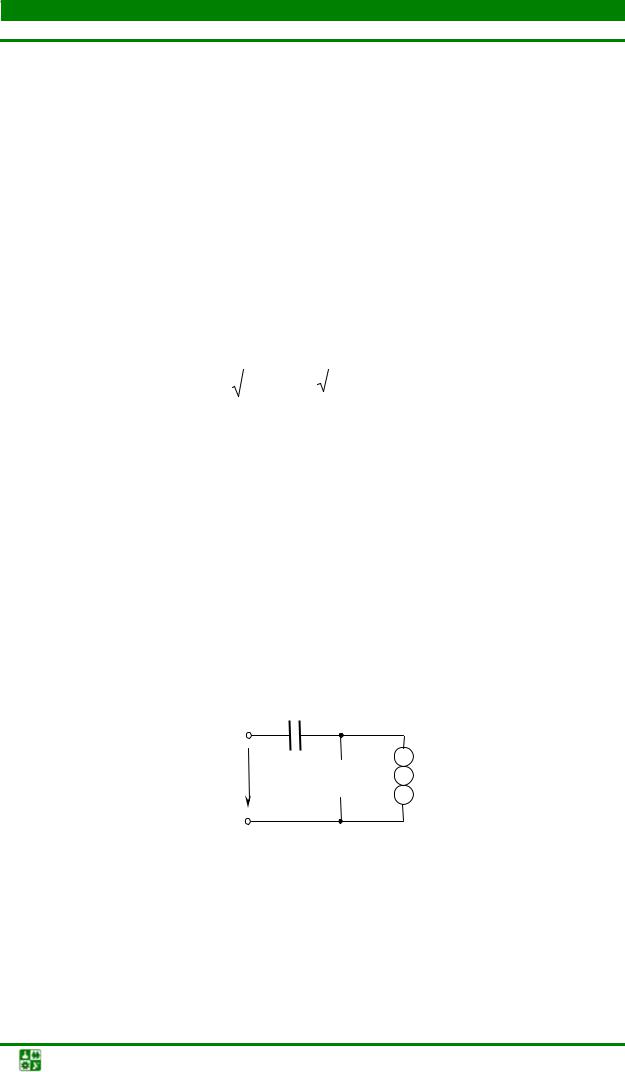
Вычислить UL в схеме рис. 2.37, если ϕ = 0, U = 180 В, UC = 300 В.
Теоретические основы электротехники. Практикум |
-84- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
|
X L |
1 |
|
IL |
|
IC |
|
U |
|
IR |
|
|
R |
XC |
|
|
|
2
Рис. 2.37
Пояснение к решению
Так как индуктивный и емкостный элементы находятся на участках цепи, соединенных между собой последовательно, ток и напряжение на входе совпадают по фазе (ϕ = 0), то наблюдается режим резонанса
напряжений.
Выявим узлы (1 и 2), ветви, направим токи.
Решение
1. Построим векторную диаграмму (рис. 2.38), начиная с вектора напряжения между двумя узлами U12 . Затем строим векторы токов в
пассивных параллельных ветвях IR и IC . Вектор тока I L равен геометрической сумме векторов IR и IC . Входное напряжение складывается
из векторов напряжений U |
и U |
L |
и совпадает с вектором входного тока |
I |
L |
|||||||||
|
|
|
12 |
|
|
|
|
|
|
|
||||
по фазе. Напряжение U L опережает ток I L на 90°. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
UL |
|
|
|
|
|
|
|
|
|
|
|
IL |
|
IC |
|
|
||
|
|
|
|
|
|
|
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
|
|
IR |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
12 |
|
|
|||
|
|
|
|
|
|
|
Рис. 2.38 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
2. Из прямоугольного |
треугольника |
напряжений, учитывая, |
что |
|||||||||||
U12 =UC , вычислим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
L |
= |
|
U 2 |
−U 2 |
= |
3002 −1802 |
= 240 В. |
|
|
||||
|
|
12 |
|
|
|
|
|
|
|
|
|
|
||
Задача3
Вычислить все сопротивления схемы рис. 2.37, если Р = 200 Вт,
Теоретические основы электротехники. Практикум |
-85- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
U = 40 В, UL =30 В, U12 = 50 В, ϕ = 0.
Решение
1. Вычислим ток I L , воспользовавшись формулой активной мощности
P =U IL cosφ =U IL .
Отсюда |
IL = |
P |
= 200 = 5 А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
U |
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2. |
Определим ток IR , исходя из того, |
что потребителем мощности |
|||||||||||||||||||||
является резистор, поэтому |
P =U I |
R |
. Тогда |
I |
R |
= |
|
P |
= 200 = 4 А. |
||||||||||||||
U |
|||||||||||||||||||||||
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
50 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
||
3. |
Вычислим ток IC с помощью треугольника токов (рис. 2.38): |
||||||||||||||||||||||
|
|
|
|
|
IC = |
IL2 − IR2 |
= |
52 − 42 |
=3 А. |
|
|||||||||||||
4. |
Определим сопротивления приемников: |
|
|
|
|
|
|
||||||||||||||||
X L |
= |
U L |
= |
30 = 6 Ом, |
R = U12 = |
50 =12,5 |
|
Ом, |
|
XC = U12 =16,7 Ом. |
|||||||||||||
|
|
|
|||||||||||||||||||||
|
|
IL |
5 |
|
IR |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
IC |
||||
Обратите внимание! |
Входное реактивное сопротивление X = 0, но |
||||||||||||||||||||||
X L = XC |
только в частном случае, при непосредственном последовательном |
||||||||||||||||||||||
соединении индуктивной катушки и конденсатора. |
|
|
|
||||||||||||||||||||
Следующую задачу решите самостоятельно. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
Задача4 |
|
|
|
|
|
|
|
|||||||||
Вычислить UL в схеме рис. 2.39, если U = 75 В, UC =100 В, ϕ = 0. |
|||||||||||||||||||||||
|
|
|
|
|
|
|
XC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
U |
|
|
|
|
R |
|
|
|
|
|
|
X L |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Рис. 2.39 |
|
|
|
|
|
|
|
|||||||||
Ответ: U L =125 В. |
|
Задача5 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
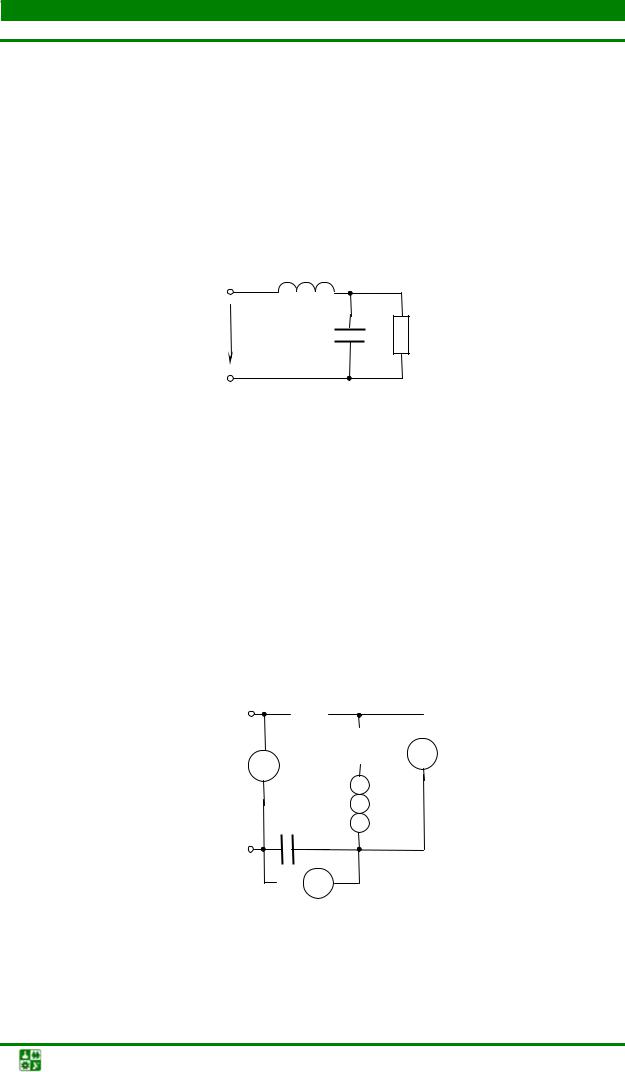
Вычислить емкость конденсатора С и входной ток I в схеме рис. 2.40, |
|||||||||||||||||||||||
если U = 120 В, ω=800 с-1, R = 5 Ом, R = 3 Ом, |
|
X |
L |
|
= 2 Ом, ϕ = 0. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Теоретические основы электротехники. Практикум |
-86- |

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
I |
XC |
1 |
|
|
|
||
U |
|
R |
R1 |
|
|
||
|
|
|
|
|
|
X L |
|
2
Рис. 2.40
В условии даны значения параметров схемы, следовательно, для решения нужно использовать условие резонанса напряжений: Xэ = 0 .
Решение
1. Запишем эквивалентное комплексное сопротивление схемы:
|
Z э = − j XC + |
(R + j X L ) R1 = |
|
|
|||||
|
|
|
|
|
|
R + j X L + R1 |
|
|
|
= − j X C + |
|
(5 + j 2) 3 |
= |
= − j X C + |
5,38e j21°50′ |
3 |
= |
||
|
5 + j 2 |
+3 |
|
8,25e j14° |
|
||||
|
|
|
|
|
|
|
|||
= − j X C +1,96e j7°50′ |
= − j X C +1,94 + j 0,27. |
|
|||||||
2. Эквивалентное реактивное сопротивление является мнимой составляющей (без j) комплексного сопротивления:
Xэ = −XC + 0,27 = 0.
Отсюда X C = 0,27 Ом. |
|
|
|
Емкость конденсатора C = |
1 |
= 0,0046 Ф. |
|
XC ω |
|||
|
|
3. Эквивалентное комплексное сопротивление цепи является чисто активным:
Z э = Rэ =1,94 Ом.
Теоретические основы электротехники. Практикум |
-87- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
4. Вычислим ток в цепи по закону Ома: I = U = 120 = 62 А.
Rэ 1,94
Следующую задачу решите самостоятельно.
Задача6
Эквивалентное комплексное сопротивление цепи, схема которой представлена на рис. 2.41, чисто активное и Z э = Rэ =125 Ом.
X L
U |
XC |
R |
Рис. 2.41
Определить индуктивность катушки L и емкость конденсатора С, если
сопротивление R = 200 Ом, циклическая частота ω= 2 105 с-1. Ответ: L = 0,484 мГн; C = 0,0194 мкФ.
Задачи 7–10 решите для самоконтроля. |
|
|
|
||||||||
|
Задача7 |
|
|
|
|||||||
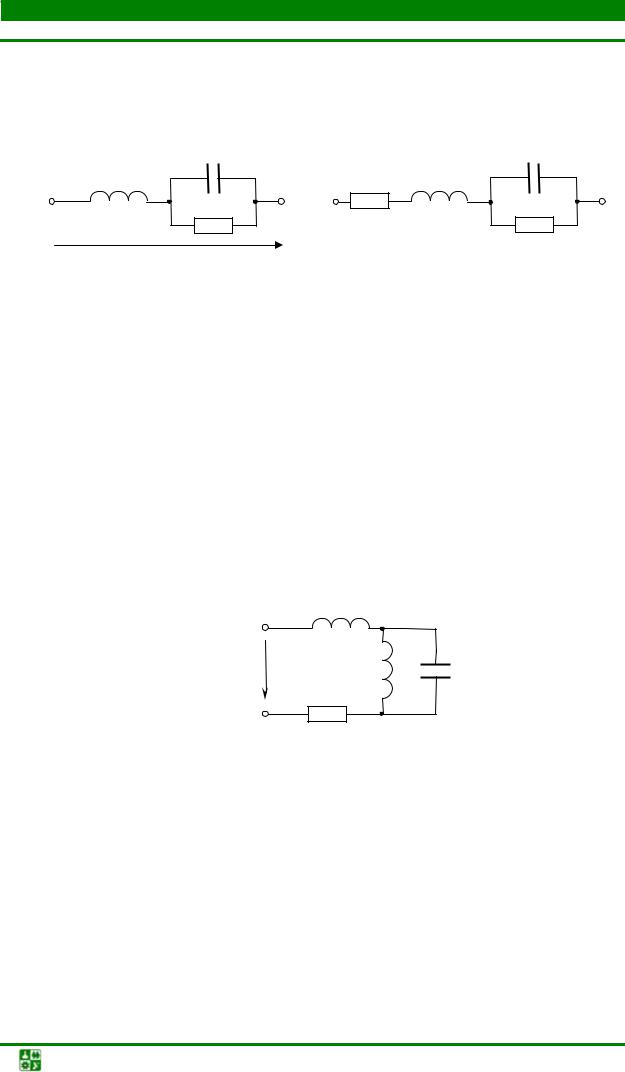
Вычислить параметры схемы (рис. 2.42), если ϕ = 0, |
I = 4 А, f = 50 |
||||||||||
Гц, вольтметры показывают соответственно: |
U = 200 |
В, U1 = 206 В, |
|||||||||
U2 =180 В. |
|
|
|
||||||||
|
|
|
R |
|
|
|
|||||
|
|
|
|
|
|
|
|
R1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
V1 |
|
|||||||
|
XC |
|
|
|
X L |
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
V2 |
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
Рис. 2.42 |
|
|
|
|||||
Ответ: R = R1 = 25 Ом; |
|
|
|
||||||||
С = 70 мкФ; L = 0,143 Гн. |
|
|
|
||||||||
Теоретические основы электротехники. Практикум |
-88- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
Задача8
Вычислить U в схеме (рис. 2.43), если ϕ = 0, UC =150 В, U L =120 В,
XC |
|
|
XC |
X L |
R |
|
X L |
|
1 |
|
R |
R |
|
|
|
U |
|
|
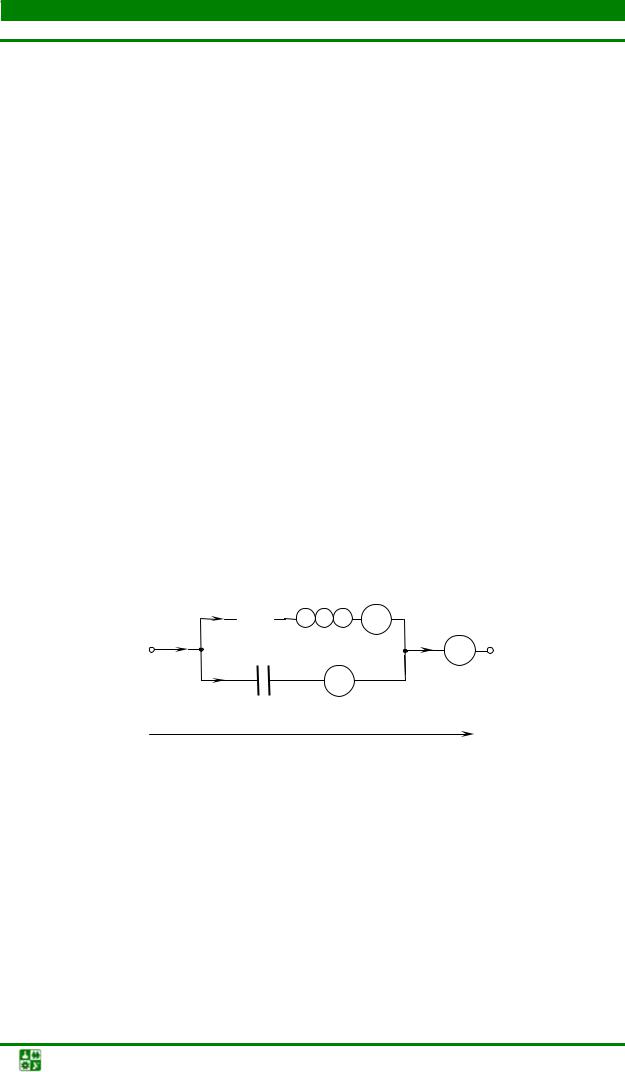
Рис. 2.44 |
Рис. 2.43 |
|
|
|
Ответ: U = 90 В. |
|
|
|
|
Задача9 |
|
|
Вычислить X L в схеме, |
представленной |
|
на рис. 2.44, если X C = |
= R = 5 Ом, R1 =8 Ом, ϕ = 0. |
|
|
|
Ответ: X L = 2,5 Ом. |
|
|
|
|
Задача10 |
|
|
Вычислить L0 в схеме (рис. 2.45), если ϕ = 0, R = 2 Ом, L = 2 мГн, |
|||
C = 250 мкФ, ω= 2 103 с-1. |
|
|
|
|
L0 |
|
|
|
u |
L |
С |
|
R |
||
|
|
|
|
|
Рис. 2.45 |
|
|
Ответ: L0 = 2 мГн. |
|
|
|
Занятие2
Цели занятия:
1.Научиться строить векторные диаграммы при резонансе токов.
2.Научиться использовать условие резонанса для расчета цепей при параллельном соединении приемников.
Теоретические основы электротехники. Практикум |
-89- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
Алгоритм построения векторных диаграмм подробно рассмотрен на с. 45 и 63. Так как при резонансном режиме сопротивление цепи чисто активное, направления векторов входного тока и входного напряжения совпадают.
Если в условии задачи заданы параметры схемы (R,L,C), для решения
необходимо использовать условие резонанса.
При резонансе токов в цепи с параллельным соединением индуктивных катушек и конденсаторов входная реактивная проводимость В = 0.
Реактивную проводимость ветви определяют по формуле
|
|
|
B = |
|
X |
, |
|
|
|
|||
|
|
R2 + X 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
где X и R – соответственно реактивное и активное сопротивления этой |
||||||||||||
ветви. |
|
|
|
|
|
|
|
|
|
|
|
|
Если ветвь не обладает активным сопротивлением |
(R = 0 ), то |
|||||||||||
реактивная проводимость B = |
1 |
, где |
X = X L − X C . |
|
|
|||||||
|
|
|
||||||||||
|
|
X |
|
|
|
|
|
|
|
|||
Рассмотрим алгоритмы решения целевых задач на конкретных |
||||||||||||
примерах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача1 |
|
|
|
|
|
|||
Определить показания второго амперметра (рис. 2.46), если в |
||||||||||||
резонансном режиме остальные приборы показывают: |
I1 = 6 А, |
I3 =3,6 А. |
||||||||||
|
R |
|
X L |
|
|
|
|
|
||||
I |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
A1 |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
I |
XC |
|
|
|
|
|
3 |
A3 |
|
|||
|
|
|
|
|
|
|||||||
I2 |
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U
Рис. 2.46
Решение
1. Построим векторную диаграмму (рис. 2.47).
Теоретические основы электротехники. Практикум |
-90- |

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
I3
. U
I1 I2
Рис. 2.47
2. Вычислим ток I2 :
I |
2 |
= |
I 2 |
− I 2 |
= |
62 −3,62 |
= 4,8 А. |
|
|
1 |
3 |
|
|
|
|
|
|
|
|
Задача2 |
|
||
Вычислить сопротивления всех приемников в схеме, представленной |
|||||||
на рис. 2.46, если Р = 80 Вт, |
I1 = 5 А, I3 = 4 А, |
φ = 0. |
|||||
Решение
1. Вычислим ток I2 из треугольника токов (рис. 2.47):
I2 = 
 I12 − I32 =
I12 − I32 = 
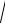 52 − 42 =3 А.
52 − 42 =3 А.
2. Определим входное напряжение, воспользовавшись формулой активной мощности:
P =U I3 cosϕ =U I3 .
Отсюда U = P = 80 = 20 В.
I3 4
3. Вычислим активное сопротивление, воспользовавшись формулой
P = R I12 . Тогда R = P = 80 =3,2 Ом.
I12 52
4. Вычислим полное сопротивление индуктивной катушки по закону
Ома:
Теоретические основы электротехники. Практикум |
-91- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
ZK = U = 20 = 4 Ом.
I1 5
5. Рассчитаем индуктивное сопротивление:
X L = 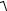
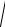 ZK2 − R2 =
ZK2 − R2 = 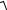
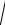 42 −3,22 = 2,4 Ом.
42 −3,22 = 2,4 Ом.
6. Вычислим емкостное сопротивление:
|
XC = U = |
20 = 6,7 Ом. |
|
|||||||
|
|
|
I2 |
3 |
|
|
|
|
||
Следующую задачу решите самостоятельно. |
|
|||||||||
|
|
|
Задача3 |
|
|
|
||||
Определить емкость конденсатора в схеме (рис. 2.46), если напряжение |
||||||||||
U = 30 В, токи I =375 мА и I |
3 |
= 225 мА, ω= 5 103 с-1. |
|
|||||||
1 |
|
|
|
|
|
|
|
|
|
|
Ответ: C = 2 10−6 |
Ф. |
|
|
|
|
|
|
|
|
|
|
|
|
Задача4 |
|
|
|
||||
Вычислить емкостное сопротивление |
XC и ток I |
в схеме (рис. 2.48), |
||||||||
если U = 50 В, R1 =8 Ом, R2 =5Ом, |
X L =6 Ом, ϕ = 0. |
|
||||||||
|
|
I |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
R |
|
R2 |
|
|
|
|
|
|
|
|
|
|
||
|
U |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
X L |
|
XC |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.48 |
|
|
|
||||
|
|
|
Решение |
|
|
|
||||
1. Вычислим XC |
из условия |
резонанса токов: |
входная реактивная |
|||||||
проводимость B = 0. Схема содержит две параллельные ветви с разным характером реактивных сопротивлений. Поэтому B = BL − BC = 0 и BL = BC .
Индуктивная проводимость
Теоретические основы электротехники. Практикум |
-92- |

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
BL = X 2X+LR2
L 1
Емкостная проводимость
BC = X 2X+CR2
C 2
Подставив эти значения, получим следующее уравнение:
6 |
|
= |
XC |
; |
36 + |
64 |
XC2 + 25 |
6XC2 −100XC +150 = 0.
Найдем корни этого уравнения:
XC |
= |
100 ± |
10000 −6 4 150 |
= |
100 ± |
6400 |
= |
100 ±80 |
; |
1,2 |
|
|
2 6 |
|
12 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
XC |
= |
100 +80 |
=15 |
Ом; |
XC =1,67 Ом. |
||
|
12 |
||||||
1 |
|
|
|
2 |
|||
|
|
|
|
|
|||
Полученное решение означает, что резонанс токов возможен при двух значениях емкостного сопротивления.
2. Вычислим ток в неразветвленной части схемы по закону Ома для действующих значений:
I = Y U .
Полная проводимость Y при резонансе токов является чисто активной:
Y =G =G |
+G |
= |
|
R1 |
+ |
|
R2 |
|
1 |
2 |
|
X 2 |
+ R2 |
|
X 2 |
|
+ R2 |
|
|
|
L |
1 |
|
С |
2 |
|
При XC1 =15 Ом активная проводимость
G = |
8 |
+ |
5 |
= 0,1 См. |
|
36 +64 |
225 + 25 |
||||
|
|
|
Тогда ток I = G U = 0,1 50 = 5 А.
При ХС2 =1,67 Ом активная проводимость
Теоретические основы электротехники. Практикум |
-93- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
G = 1008 + 275,8 = 0,26 См.
Ток I = 0,26 50 =13 А.
Задача5
Вычислить I,U, B2, ω в схеме (рис. 2.49), если ϕ = 0, I1 =1 А, I2 = 0,8 А, Q2 =32 вар, L = 25 мГн.
I |
R |
XC |
1 |
|
|
I |
|
X L |
|
I2 |
|
|
|
|
|
|
U |
Рис. 2.49
Решение
1. Вычислим ток I из треугольника токов, который получается при построении векторной диаграммы (рис. 2.50):
I = 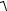
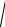 I12 − I22 =
I12 − I22 = 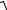
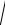 12 −0,82 = 0,6 А.
12 −0,82 = 0,6 А.
I |
I2 |
|
1 |
||
|
||
I |
|
|
Рис. 2.50 |
U |
|
|
||
2. Вычислим входное напряжение, воспользовавшись формулой |
||
реактивной мощности Q2 =U I2 . |
|
|
Отсюда U = Q2 = 32 = 40 В.
I2 0,8
3. Вычислим индуктивную проводимость по закону Ома:
Теоретические основы электротехники. Практикум |
-94- |
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
|
|
|
|
|
B = |
I2 |
= |
0,8 |
= 0,02 См. |
||||||||
|
|
|
|
|
|
|
40 |
|
|||||||||
|
|
|
|
|
2 |
U |
|
|
|
|
|
|
|||||
|
4. Вычислим циклическую частоту ω: |
||||||||||||||||
|
|
|
|
|
|
|
|
B = |
|
|
1 |
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
Lω |
||||
Тогда |
ω= |
1 |
= |
103 |
= 2000 с |
-1 |
. |
|
|
|
|
|
|
|
|
||
B L |
0,02 25 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача6 |
|||||||||
|
Вычислить I1,U,Y1, X L в схеме (рис. 2.51), если I = 0,4 А, I2 = 0,7 А, |
||||||||||||||||
G1 = 0,08 См, R = 3 Ом, ϕ = 0. |
|
|
|
|
|
|
|
|
|
|
X L |
||||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|||||
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
XC |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
||
|
|
|
|
|
|
|
|
|
Рис. 2.51 |
||||||||
Решение
1. Вычислим ток I1 из треугольника токов (см. рис. 2.47):
I1 = 
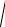 I 2 + I22 =
I 2 + I22 = 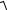
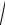 0,42 + 0,72 = 0,8 А.
0,42 + 0,72 = 0,8 А.
2. Вычислим входное напряжение по закону Ома:
I =Y U =G1 U.
Отсюда U = |
I |
= |
0,4 |
=5 В. |
|
G |
0,08 |
||||
|
|
|
|||
|
1 |
|
|
|
3. Вычислим полную проводимость первой ветви по закону Ома:
Y1 = UI1 = 05,8 = 0,16 См.
Теоретические основы электротехники. Практикум |
-95- |

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
4. Вычислим полное сопротивление первой ветви:
|
|
|
|
Z = |
1 |
= |
1 |
= 6,25 |
Ом. |
||||
|
|
|
|
0,16 |
|||||||||
|
|
|
1 |
Y |
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5. Вычислим индуктивное сопротивление: |
|||||||||||||
|
|
|
|
|
|
=5,48 Ом. |
|||||||
|
X |
L |
= |
Z 2 |
− R2 |
= |
6,252 −32 |
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Задача7 |
|
|
|||
Вычислить активное |
сопротивление |
R в схеме (рис. 2.51), если |
|||||||||||
I = 0,8А, Z = 4 |
Ом, B |
= 0,3 См, ω =105 с-1, ϕ = 0. |
|||||||||||
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
Решение
Можно предложить несколько вариантов для решения этой задачи. Рассмотрим наиболее рациональные и интересные.
Вариант I.
1. Вычислим потребляемую мощность по формуле
P= Z I 2 = 4 0,82 = 2,56 Вт.
2.Вычислим напряжение U по закону Ома:
U= Z I = 4 0,8 = 3,2 В.
3.Вычислим ток I2 по закону Ома:
I2 = B2 U .
Из условия резонанса токов B1 = B2 , поэтому
I2 = 0,3 3,2 = 0,96 А.
4. Вычислим ток I1 из треугольника токов (см. рис. 2.47):
I = |
I 2 |
+ I 2 |
= |
0,82 + 0,962 |
=1,25 А. |
1 |
|
2 |
|
|
|
5. Вычислим активное сопротивление R из формулы активной мощности: P = R I12 .
Теоретические основы электротехники. Практикум |
-96- |

ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
Отсюда
R = P = 2,56 =1,63 Ом.
I12 1,252
Вариант II.
1. Вычислим активную проводимость G1. При резонансе токов G1 равна полной проводимости цепи Y :
G1 =Y = Z1 = 0,25 См.
2. Вычислим полную проводимость ветви с индуктивной катушкой:
Y1 = 
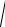 G12 + B12 =
G12 + B12 = 
 0,252 + 0,32 = 0,39 См.
0,252 + 0,32 = 0,39 См.
3. Вычислим активное сопротивление по формуле
R = G1 = 0,25 =1,63 Ом.
Y12 0,392
Следующие задачи решите самостоятельно.
|
Задача8 |
|
|
||
Вычислить I2 ,U, P,Y1 в |
схеме рис. 2.51, еслиI1 =1,5 |
А, |
I =1,2 А, |
||
B1 = 0,03 См, ϕ = 0. |
|
|
|
|
|
Ответ: I2 = 0,9 А, U = 30 В, P = 36 Вт, Y1 = 0,05 См. |
|
|
|||
|
Задача9 |
|
|
||
Вычислить I, I1, I2 ,C в схеме рис. 2.51, если G1 = 0,2 См, |
B2 =0,5 См, |
||||
U = 2 В, ω=105 с-1, ϕ = 0. |
|
|
|
|
|
Ответ: I = 0,4 А; I =1,08 |
А; I |
2 |
=1 А; C = 5 10−6 Ф. |
|
|
1 |
|
|
|
|
|
Задачи 10–13 предлагаются для самоконтроля. |
|
|
|||
|
Задача10 |
|
|
||
Вычислить I, B2 ,U в схеме рис. 2.51, если I1 =1 А, |
I2 = 0,8 А, |
||||
Q2 =32 вар, ϕ = 0. |
|
|
|
|
|
|
|
|
|||
Теоретические основы электротехники. Практикум |
|
-97- |
|||
ГЛАВА 2 ОДНОФАЗНЫЕ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Тема 3 Анализ резонансных режимов
Ответ: I = 0,6 А; B2 = 0,02 См; U = 40 В.
|
|
Задача11 |
|
Вычислить |
I,U,Y1,C |
в схеме рис. 2.51, если I1 = 3 А, I2 =1,8 А, |
B1 = |
0,09 См, ϕ = 0, f |
= 50 Гц. |
|
|
Ответ: I = 2,4 А; U = 20 В; Y1 = 0,15 См; C = 287 мкФ. |
|
||
|
|
Задача12 |
|
Определить емкость конденсатора С в схеме рис. 2.51, если R = =12 |
|||
Ом, X L =16 Ом, |
f = 50 Гц. |
|
|
Ответ: C =127 мкФ. |
|
|
|
|
|
Задача13 |
|
Вычислить U и UR |
в схеме рис. 2.52, если I1 = 2 А, C = 0,4 |
мкФ, |
|
ω= 5 104 с-1, ϕ = 0 . |
|
|
|
X L
R I1 
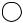
XC
UR
U
Рис. 2.52
Ответ: U =100 В; U R = 0.
Теоретические основы электротехники. Практикум |
-98- |
