ГЛАВА 9 ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
В предыдущих главах были рассмотрены цепи с сосредоточенными параметрами, в которых выделяют активные, индуктивные и емкостные элементы.
В цепях с распределенными параметрами энергии электрического и магнитного полей, а также необратимые преобразования энергии распределены вдоль длины цепи.
Занятие1
Цели занятия:
1.Научиться рассчитывать первичные параметры однородной линии.
2.Научиться вычислять вторичные параметры длинной линии.
3.Научиться определять волновые параметры линии.
Однородной называют линию, параметры которой равномерно
распределены вдоль ее длины. |
|
|
|
|
|
|
|
|||
Параметры линии |
на |
единицу |
длины |
называют |
|
первичными. Их |
||||
обозначают: R0 , G0 , C0 , L0 . |
|
|
|
|
|
|
|
|
||
R |
С= Ом м; |
G L= См м; |
[ |
0 ] |
= Ф м; |
[ 0 |
] |
= Гн м. |
||
[ 0 ] |
|
[ |
0 ] |
|
|
|
||||
Обычно их считают известными и постоянными.
Если первичные параметры не заданы, их можно вычислить по приведенным далее формулам для двухпроводной линии.
Погонная индуктивность, Гн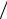
м,
L0 = µπ0 ln dr = 4 10−7 ln dr ,
где µ0 = 4π 10−7 – магнитная постоянная, Гн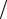
м,
r – радиус проводов линии,
d – расстояние между проводами.
Нужно отметить, что единицы измерения d и r должны быть одинаковыми.
Погонная емкость, Ф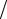
м,
C = 27,8 |
ε 10−12 , |
|
ln d |
r |
|
0 |
|
|
r |
|
|
где εr – относительная диэлектрическая проницаемость. |
|
|
|
|
|
Теоретические основы электротехники. Практикум |
-313- |
|
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Погонное активное сопротивление для меди σ =5,8 107Ом1 м
|
8,32 |
|
−6 |
1,44 |
|||
R0Гц= |
f |
||||||
r |
10Ом м = |
r |
|
Ом м. |
|||
|
λ |
||||||
|
см |
|
|
мм |
м |
||
Погонная активная проводимость, См м, |
|
|
|||||
G0 = ωC0 tg δ,
где δ – угол диэлектрических потерь.
Нужные для расчетов величины приведены в справочной литературе. Вторичными параметрами линии считают коэффициент
распространения электромагнитной волны γ и волновое сопротивление Zc .
Коэффициент распространения γ = 
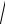Z 0 Y 0 ,
где Z 0 = R0 + jL0ω – комплексное продольное сопротивление на единицу
длины линии;
Y 0 = G0 + jC0ω – комплексная поперечная проводимость на единицу
длины линии.
Как любое комплексное число, коэффициент распространения состоит из действительной и мнимой составляющих:
γ = α + jβ,
где α – коэффициент затухания, характеризующий степень уменьшения модуля; β – коэффициент фазы, характеризующий степень изменения аргумента.
[α]= Нп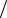
м, [β]= рад
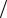м..
Волновое сопротивление
|
|
. |
Z с = |
Z 0 |
|
|
Y0 |
|
Волновыми параметрами линии являются фазовая скорость υ и длина волны λ.
Фазовая скорость – это скорость изменения фазы колебания, которая с течением времени и ростом координаты х остается неизменной. Ее определяют по формуле
υ = ωβ .
Теоретические основы электротехники. Практикум |
-314- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Если в воздушной линии пренебречь потерями, то максимальная фазовая скорость примерно равна скорости света: υ ≈ с = 3 105 км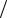
с.
Длина волны λ = 2βπ – это кратчайшее расстояние между двумя
точками, взятое в направлении распространения волны, фаза колебания которых отличается на 2π.
В линии |
без |
потерь |
(R0 = G0 = 0) коэффициент затуханияα = 0; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
υ = |
|
1 |
|
. |
|
γ =β = ω |
|
|
|
; Z |
|
= |
|
L0 |
|
= Z |
|
; |
||||||
L C |
0 |
|
c |
c |
||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|||||||||||||||||
0 |
|
|
|
|
C0 |
|
|
|
|
L0C0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если Z c , α и υ не зависят от частоты, в линии не будет искажений.
Для этого необходимо следующее соотношение параметров: L0 = R0 .
C0 G0
При этом коэффициент затухания α = αmin = 
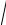R0G0 . Перейдем к рассмотрению конкретных задач.
Задача1
Рассчитать погонные параметры двухпроводной воздушной линии (tgδ = 0), составленной из медного провода диаметром 6 мм. Расстояние между проводами d = 200 мм. Рабочая частота f = 100 кГц.
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Погонная индуктивность |
|
|
|
|||||||||
L0 = 4 |
10 |
−7 |
ln |
d |
= 4 |
−7 |
200 |
=1,68 10 |
−6 |
|
||||||||||
|
|
|
r |
10Гнlnм. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||
Погонная емкость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C |
|
|
27,8ε |
r |
|
|
|
−12 |
|
27,8 1 |
−12 |
|
|
|
−12 |
|||||
|
= |
|
|
|
|
10 |
|
|
= |
Ф |
м10. |
|
|
= 6,64 |
10 |
|
||||
|
ln d |
|
|
|
|
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
ln 200 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
Погонное сопротивление
|
8,32 |
|
|
|
|
8,32 |
|
|
|
|
|
|
|
|
|
−6 |
|
|
5 −6 |
|
|
−3 |
|||
R0Гц= |
f |
|
|
|
|
|||||||
r |
10 |
|
= |
0,3 |
10Ом10м. |
=8,76 |
10 |
|
||||
|
cм |
|
|
|
|
|
|
|
|
|
|
|
Погонная проводимость |
|
|
|
|
|
|
|
|
||||
Теоретические основы электротехники. Практикум |
-315- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
G0 = ωC0tg δ = ωC0 0 = 0.
Задача2
Вычислить коэффициент распространения и волновые параметры
линии при частоте f = 1200 Гц, если R0 |
=12,4Ом км, L0 |
= 4,8 10Гн км, |
|||
|
|
|
|
|
−3 |
G0 = 0,8 |
−6 |
С0 = 5 |
−9 |
|
|
10См км, |
10Ф км. |
|
|
||
Решение
Коэффициент распространения электромагнитной волны
γ = 
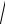Z 0 Y 0 = 
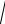(R0 + jL0ω)(G0 + jC0ω)=
= 
(12,4 + j 4,8 10−3 2π 1200) (0,8 10−6 + j5 10−9 2π 1200) =
=
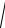(12,4 + j36,191) (0,8 10−6 + j37,699 10−6 ) =
=
38,255еj71,09° 0,0000377e j88,78° = 0,03798e j79,93° =
=(0,00664 + j0,0374)км−1.
1.Коэффициент затухания α = Re γ = 0,00664п кмH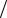 
0,05774= дБ км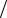 
(1 дБ = 0,115 Нп).
2. Коэффициент фазы β = Im(γ) = 0,0374рад км |
. |
3.Фазовая скорость υ = ωβ = 2βπf = 20,0374π 1200 = 201497,326км с.
4.Длина волны λ = 2βπ = 0,60374,28 =167,9 км.
Задача3
Определить первичные параметры R0 , L0 , G0 , C0 линии с волновым
сопротивлением |
Z c =100e− j15° Ом и коэффициентом распространения |
|||
γ =10 |
−3 |
j45° |
1 |
при циклической частоте ω=500рад с. |
|
eкм |
|||
Теоретические основы электротехники. Практикум |
-316- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Решение
1. Волновое сопротивление
|
|
|
|
|
|
|
|
|
|
|
|
|
Z c = |
Z 0 |
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y 0 |
|
|
|
|
|
|
|
|
|
Коэффициент распространения γ = |
|
. |
|
|
|
||||||||||||||||||||||
Z 0 Y 0 |
|
|
|
||||||||||||||||||||||||
2. |
Умножив Z c на γ, получим |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Z |
0 |
= Z |
c |
γ =100e |
− j15° |
|
−3 j45° |
= |
j30° |
( |
5 |
10+ j |
) |
−2 |
|||||||||||||
|
|
|
е 10 |
|
0,1e |
|
8,67= |
|
Ом км. |
||||||||||||||||||
Погонное сопротивление Z |
0 |
= R |
+ jL ω. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
||
Тогда R0 =8,67 |
|
|
−2 |
|
|
|
|
L0 = |
5 10−2 |
|
|
−4 |
|
|
|||||||||||||
10Ом км, |
|
|
500 |
=10Гн км. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Разделив γ на Z c , получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Y 0 |
= |
γ |
= |
10−3 e j45° |
|
=10 |
−5 |
e |
j60° |
=(См5 + jкм8,67. |
) 10 |
−6 |
|
||||||||||||
|
|
Z c |
100e− j15° |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Погонная проводимость Y |
0 |
= G + jC |
0 |
ω. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
Отсюда G = 5 10 |
−6 См |
, С |
|
= |
8,67 10−6 |
|
|
|
−8 |
|
|||||||||||||||||
км |
|
|
|
500 |
|
|
=1,73 |
10Ф км. |
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача4
Вычислить вторичные параметры и длину волны линии без потерь,
если L0 |
=14,16 10Гн км, |
G0 |
= 0,95 10См км, |
f =1800 1 c. |
|
−3 |
|
−6 |
|
Решение
1. Коэффициент затухания α = 0. Коэффициент распространения
γ =β = ω
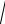L0 C0 = 2πf 
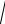L0 C0 = 2π 1800
14,16 10−3 3,4 10−9 =
=0,07847рад км.
2.Волновое сопротивление
Теоретические основы электротехники. Практикум |
-317- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
|
|
|
|
|
|
Z |
|
|
|
|
|
|
L |
|
|
|
|
|
14,16 10−3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
с |
= |
|
|
|
|
|
0 |
|
= |
|
|
|
3,4 10−9 |
|
|
= 2040,76Ом. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
|
Длина волны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
λ = |
2π = |
|
|
2π |
|
|
|
=80,07км. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0,07847 |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача5 |
|
|
|
||||||||||
Вычислить |
|
погонную |
|
|
емкость |
|
|
C0 |
линии |
с |
параметрами |
||||||||||||||||||||||||
R0 =12,4Ом км, |
|
L0 |
= 4,8 10Гн км, |
|
|
G0 = 0,8 10См км |
для передачи на |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−6 |
|
|
|
максимальное расстояние сигналов без искажения с допустимым затуханием |
|||||||||||||||||||||||||||||||||||
αl =10 дБ. Определить это расстояние. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
||||||||||
Условие линии без искажений: |
L0 |
= |
R0 |
. |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
0 |
|
|
|
G |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
Отсюда C0 = |
|
L |
G |
|
|
|
4,8 |
10−3 0,8 10−6 |
−9 |
|
|
||||||||||||||||||||||||
|
0 |
|
|
0 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0,3097 10Ф |
км. |
|
||||||||||
R0 |
|
|
|
|
|
|
|
|
|
|
12,4 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Коэффициент затухания будет минимальным: |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
α |
|
|
= |
|
|
|
|
|
|
|
=км12,4 0,8 10−6 |
= 3,15 10−3 |
. |
||||||||||||||||||||||
min |
R НпG |
||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Длина передачи сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
l |
= |
|
|
|
αl |
|
= |
|
10 0,115 = |
1150 = |
365км. |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
αmin |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,15 10−3 |
3,15 |
|
|
|
|
||||||||||||||||
Следующие задачи решите самостоятельно. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача6 |
|
|
|
||||||||||
Вычислить |
|
вторичные |
|
|
и |
волновые |
параметры линии, если |
||||||||||||||||||||||||||||
R0 =58Ом км, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−9 |
|
|
|
|
|
|
|
|
L0 = 4,24 |
−3 |
|||||
|
|
|
|
|
|
|
С0 =11,5 10Ф км, |
|
|
|
|
|
10Гн км, |
||||||||||||||||||||||
G0 =1,02 |
|
−6 |
|
|
|
|
f =10000Гц. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
10См км, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Теоретические основы электротехники. Практикум |
-318- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
|
Ответ: |
|
|
Z c = 614,259eОм; |
|
γ = 0,048 + j0,441км |
; |
−1 |
||||||
|
|
|
|
|
|
|
|
− j6,09° |
|
|
|
|
||
υ =142403,6км с; |
; λ =14,24км. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Задача7 |
|
|
|
|
|||
|
Определить |
первичные |
параметры линии, |
если |
f = 1800 |
|
Гц, |
|||||||
Z c = 2240,944eОм, |
|
γ = |
0,086e |
j72,29° |
1 |
|
|
|
|
|||||
|
км. |
|
|
|
|
|||||||||
|
Ответ: |
− j16 29° |
|
|
|
|
|
|
|
|
|
|
||
|
R =108Ом км; |
L =14,16 |
10Гн км; |
G = 0,95 10См км, |
|
|||||||||
|
|
|
0 |
|
|
|
0 |
|
|
−3 |
0 |
−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С = 3,4 10Ф−9 |
км. |
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача8 |
|
|
|
|
|||
|
Определить |
значение |
G |
, |
при |
котором линия будет передавать |
||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
сигналы |
без искажения, |
если |
|
R0 =58Ом км, |
С0 =11,5 10Ф−9 км, |
|
||||||||
L |
= 4,24 |
−3 |
|
. |
|
|
|
|
|
|
|
|
|
|
10Гн км |
|
|
|
|
|
|
|
|
|
|
||||
0 |
Ответ: G =157,3 10См км. |
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
−6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача9 |
|
|
|
|
|||
|
Вычислить коэффициент затухания, коэффициент фазы, фазовую |
|||||||||||||
скорость и длину волны линии при частоте ω=10−4с1 |
при следующих |
|||||||||||||
значениях |
первичных параметров: |
R =10Ом км; , |
L = 0,5мГн км, , |
|||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
С0 |
|
−8 |
|
|
−6 |
|
|
|
|
|
|
|
|
|
= 4 10Ф км, |
G0 =10См км. |
|
|
|
|
λ =110,56 |
|
|
||||||
|
Ответ: |
α = 0,0352Нп км, |
|
β = 0,0568рад км, |
|
км, |
||||||||
υ=176056км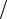 
с.
Занятие2
Цели занятия:
1.Научиться находить токи и напряжения в различных сечениях линии при заданных нагрузках.
2.Изучить особенности расчетов токов и напряжений в линии без
потерь.
3.Научиться определять мощности в различных сечениях линии и КПД линии.
Напряжение и ток в любой точке линии, если задан режим работы на входе линии, можно определить из следующей системы уравнений:
Теоретические основы электротехники. Практикум |
-319- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
I = I2cosβx + j U2 sinβx .
Z c
Для расчета мощностей удобно пользоваться формулой комплексной
*
мощности S =U I = Р+ jQ .
Полная мощность является модулем комплексной мощности S. Активная мощность P = Re(S) , реактивная мощность Q = Im(S).
Коэффициент полезного действия линии равен отношению активной мощности нагрузки (в конце линии) к активной мощности на входе линии:
η = Р2 .
Р1
Рассмотрим ряд конкретных задач.
Задача1
Определить напряжение U2 , ток I2 , мощность P2 в нагрузке, а также КПД передачи энергии по линии длиной 500 км, если напряжение на входных зажимах линии U1 = 220 кВ, волновое сопротивление Z c = 308,8e− j8°
Ом, сопротивление нагрузки |
Z н = 2Z c, коэффициент |
распространения |
||
γ = (0,1792 + j1,052) км10−.3 1 |
|
|
|
|
|
|
Решение |
|
|
1. Напряжение на нагрузке для заданного режима U2 |
= Z нI2 = 2Z cI2 . |
|||
Тогда уравнения (3) примут вид: |
|
|||
U |
=U |
2 |
( chγl +0,5shγl ); |
|
1 |
|
|
|
|
I1 = I2( chγl + 2shγl ).
Отсюда
|
|
U |
|
|
U2 |
= |
1 |
|
. |
chγl + 0,5sh |
|
|||
|
|
γl |
||
Расчет гиперболических функций:
Теоретические основы электротехники. Практикум |
-321- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
|
η= |
85052 |
= 0,87 или η=87 %. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
97746 |
|
|
|
|
|
|
|
|
|
Задача2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Линия |
с |
|
параметрами |
|
|
G0 |
= 5 10См км, |
|
|
−3 |
, |
|||||||||||||||||||||
|
|
|
L0 =8 10Гн км |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−8 |
|
|
|
|
|
||
R = 40Ом км |
и |
С = 5 10Ф−9 км |
|
длиной l = 200 км работает на частоте |
||||||||||||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = 5000с |
−1 . Определить мощности, потребляемые на входе и выходе линии, |
|||||||||||||||||||||||||||||||
если к входным зажимам линии |
|
|
приложено |
напряжение U1 =10В , |
а |
|||||||||||||||||||||||||||
сопротивление нагрузки Z н =1000e j30° Ом. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|||||||||
1. |
Вычислим волновые сопротивления Z c : |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 + j8 |
10−3 5 |
103 |
|
|
|
||||
|
|
|
|
Z |
|
|
|
|
|
|
R |
+ jL |
|
ω |
|
|
|
|
|
|
||||||||||||
|
Z c |
= |
|
|
0 |
= |
|
|
0 |
0 |
|
|
|
= |
|
|
|
|
|
|
|
|
= |
|
||||||||
|
|
|
|
|
G0 + jC0ω |
|
|
5 10−8 + j5 10−9 |
103 |
|
||||||||||||||||||||||
|
|
|
|
Y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
40 + j40 |
|
|
= |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 10−8 + j25 10−6 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
= |
|
|
|
40 |
2e j45° |
|
|
=1504e |
− j22,5° Ом. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
2,5 10−5e j90° |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2. |
Вычислим коэффициент распространения γ: |
|
|
|
|
|||||||||||||||||||||||||||
γ = Z 0 Y 0 =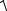 
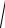40
2 e j45° 2,5 10−5 e j90° = 3,76 10−2 e j67,5° =
=(1,439 + j3,474)км10.−2 1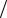
3.Вычислим напряжение U2 из системы уравнений (3):
U2 = |
U |
1 |
|
. |
|
|
|
|
|||
chγl + |
Z c |
Shγl |
|||
|
|
|
|||
|
|
Z н |
|
||
Выполним вспомогательные расчеты:
Теоретические основы электротехники. Практикум |
-323- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
|
|
|
|
|
Z c |
1504e− j22,5° |
=1,504e |
− j52,5°; |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Z н |
|
1000e j30° |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γl = 2,878 + j6,948; |
|
|
|
|
|
||||
|
eγl |
= e2,878 e j6,948° =17,78e j38,09° =13,99 + j10,98; |
|||||||||||||||||||||||
|
|
e−γl |
= |
|
1 |
|
|
|
= 0,056e− j38,09° = 0,044 − j0,0345; |
||||||||||||||||
|
|
|
eγl |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
shγl = 0,5(eγl −e−γl ) = 6,98 + j5,5 = 8,886e j38,23°; |
||||||||||||||||||||||||
|
chγl = 0,5(eγl |
+ e−γl ) = 7,015 + j5,47 =8,895e j37,94° ; |
|||||||||||||||||||||||
|
|
chγl |
+ |
Z c |
|
shγl =19,95 + j2,17 = 20,07e |
j6,22°. |
||||||||||||||||||
|
|
Z н |
|
|
|
||||||||||||||||||||
Подставив найденные значения, получим: |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
− j6,22° В. |
|||||||||
|
|
|
|
U2 |
= |
|
|
|
|
|
|
= 0,498e |
|
|
|
|
|
|
|||||||
|
|
|
20,07e j6,22° |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Комплекс тока в нагрузке |
|
|
|
|||||||||||
|
|
|
U2 |
|
|
|
|
|
0,498e− j6,22° |
|
|
|
|
−3 |
|
− j36,22° А. |
|||||||||
|
I2 |
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
0,498 10 |
|
e |
|
|
|||
4. Ток |
|
Z н |
|
|
|
|
1000e j30° |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
U2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
I |
= I |
chγl + |
|
shγl = 0,498 10−3 e− j36,22° 8,895e j37,94° + |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||
1 |
|
2 |
|
|
|
|
|
|
|
Z c |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
+0,498e−jj6,22, ° 8,886e j38,23° = 6,635 10−3e j22,38° А. 1504e− 22 5°
5.Вычислим мощности, потребляемые на входе и выходе линии:
P1 |
= Re U1 |
I |
1 |
|
=(10 6,635 10 |
−3 |
e |
− j22,38° |
)= 61,35 10 |
−3 |
Вт; |
|
|
* |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Теоретические основы электротехники. Практикум |
-324- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
P2 = Re U2 |
I2 |
= Re(0,498e |
− j6,22° |
0,498 10 |
−3 |
e |
j36,22° |
)= 0,215 |
10 |
−3 |
Вт. |
|||
|
* |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следующую задачу решите самостоятельно. |
|
|
|
|
|
|||||||||
|
|
|
|
|
Задача3 |
|
|
|
|
|
|
|
|
|
Рассчитать напряжение |
U |
и |
ток I |
в начале линии, |
комплексную |
|||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
мощность в начале и конце линии, КПД линии, если f = 1200 Гц, l = 142 км,
R0 =12,4Ом км , |
С0 = 5 10Ф км |
, |
|
|
L0 = 4,8 10Гн км, |
|||||
|
|
|
|
|
−9 |
|
|
|
|
−3 |
−6 |
|
U2 = 28,2 В, |
|
Z н =500e |
− j8,5 |
Ом. |
|
|
||
G0 = 0,8 10См км, |
|
|
|
=11,205 − j3,116ВА; |
||||||
Ответ: U =109,721eВ; |
I |
|
= 0,106e |
− j 44,467° |
А; S |
|
||||
|
1 |
− j60,011° |
1 |
|
|
1 |
|
|||
|
|
|
|
|
|
|
||||
S2 =1,572 − j0,235 ВА; η=14 %. |
|
|
|
|
|
|
|
|||
|
|
|
Задача4 |
|
|
|
|
|
||
Определить напряжение U |
и ток I |
в начале линии, а также длину |
||||||||
|
|
|
1 |
|
1 |
приняв условие: R0 = G0 = 0 , |
||||
электромагнитной |
волныλ для |
задачи 3, |
||||||||
Z н = 500 Ом. |
|
|
|
|
|
|
|
|
|
|
Решение
1. Для линии без потерь волновое сопротивление
|
|
|
|
4,8 |
10−3 |
|
|
|
|
L |
|
||||
Z c = |
0 |
= |
|
|
= 979,796 Ом. |
||
|
|
C0 |
5 10−9 |
|
|||
2. Коэффициент распространения волны
γ = jβ = ω
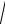L0 C0 = 2πf 
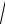L0 C0 = = 7539,822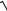
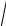4,8 10−3 5 10рад−9 = 0,0369км
3. Ток I2 |
= |
U2 |
= |
28,2 |
= 0,0564 |
А. |
|
Z н |
500 |
||||||
|
|
|
|
|
4. Вычислим напряжение U1 из системы уравнений (4):
U1 =U2cosβl + jI2 Z csinβl =
Теоретические основы электротехники. Практикум |
-325- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
=28,2cos( 0,03693 142 ) + j0,0564 979,796 sin( 0,0369 142 ) =
=14,294 − j47,635 = 49,733e− j73,297° В.
5.Вычислим входной ток I1:
I1 = I2cosβl + j U2 sinβl = 0,0564e j8,5°cos( 0,0369 142 ) +
Z c
+ j 97928,796,2 sin( 0,0369 142 ) = 0,0286 − j0,0248 = 0,0378e− j40,926° А.
6. Длина электромагнитной волны
λ = 2βπ =170,276 км.
Следующую задачу решите самостоятельно.
|
Задача5 |
|
|
|
|
|
Определить напряжение U |
и ток I |
|
в начале линии без потерь, если |
|||
1 |
1 |
|
км, |
L0 |
=14,16 10Гн км, |
|
f = 1800 Гц, l = 47,1 км, |
C0 = 3,4 |
10Ф |
||||
|
|
|
−9 |
|
|
−3 |
I2 = 6 e j16,15° мА, Z н = 4000 Ом.
Ответ: U1 = 21,4e− j146,3°В; I1 =8,022e− j113,3°мА.
Занятие3
Цели занятия:
1.Научиться определять входное сопротивление линии в разных режимах.
2.Изучить особенности расчета линии без потерь.
Входное сопротивление линии равно отношению напряжения к току на входе линии:
Z вх = U1 .
I1
Теоретические основы электротехники. Практикум |
-326- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Введение понятия входного сопротивления позволяет заменить рассмотрение цепей с распределенными параметрами цепями с сосредоточенными параметрами.
В общем случае входное сопротивление
U2chγl + Z cI2shγl |
|
Z н + Z cthγl |
. |
|||
Z вх = Z c |
|
|
|
= Z c |
|
|
|
|
|
Z c + Z нthγl |
|||
U |
2shγl + Z cI2chγl |
|
|
|||
При согласованной |
нагрузке |
(Z н = Z c ) входное сопротивление |
||||
Z вх = Z c .
Входное сопротивление линии в режиме короткого замыкания (Z н = 0)
Z вх = Z cthγl .
Входное сопротивление линии в режиме холостого хода (Z н = ∞)
Z вх = Z cchγl .
Входное сопротивление можно определить из режимов холостого хода и короткого замыкания:
Z вх = Z хх |
Z н + Z кз |
. |
|
||
|
Z н + Z хх |
|
В линии без потерь гиперболические функции заменяют круговыми тригонометрическими функциями.
Входное сопротивление имеет вид
Z вх = Z c |
Z н + jZ сtgβl |
. |
|
||
|
Z с + jZ нtgβl |
|
Напряжение и ток в разомкнутой линии без потерь определяют по следующим формулам:
U =U2cosβx,
U
I = j Z 2 Eβx,
c
где х – расстояние от конца линии до точки, в которой рассчитывают напряжение и ток.
Теоретические основы электротехники. Практикум |
-327- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Входное сопротивление линии без потерь в режиме холостого хода – реактивное:
Z вх = − jZ cctgβl .
Напряжение и ток закороченной на конце линии без потерь
|
|
|
U = jZ cI2sinβx, |
||
|
|
|
|
||
I |
= I2 cosβx. |
|
Входное сопротивление закороченной на конце линии также |
||
реактивное: |
Z вх = jZ ctgβl. |
|
|
||
Перейдем к рассмотрению конкретных задач. |
||
|
|
Задача1 |
Определить вторичные параметры однородной линии длиной 200 км при частоте f = 800 Гц, если входное сопротивление в режиме холостого хода
Z хх = 750е− j26°Ом, а в режиме короткого замыкания – Z кз = 500 Ом.
Решение
Входное сопротивление в режиме короткого замыкания
Z кз = Z cthγl ,
в режиме холостого хода – Z хх = Z ccthγl = thZγcl .
Перемножив эти выражения, получим
Z c = 
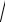Z хх Z кз = 
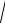750e− j26° 500 = 612,37e− j13° Ом.
Поделив Z кз на Z хх , получим
|
|
|
|
|
|
|
|
|
thγl = |
Z кз |
= |
|
500 |
|
= 0,8165e j13° . |
||
|
750e− j26° |
|||||||
|
|
Z хх |
|
|
||||
Гиперболический тангенс
Теоретические основы электротехники. Практикум |
-328- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
thγl = |
shγl |
|
= |
eγl −e |
−γl |
|
eγl |
= |
e2γl |
−1 |
. |
|
||
chγl |
eγl + e−γl |
eγl |
e2γl |
+1 |
|
|||||||||
|
|
|
|
|
|
|
||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2γl =1 + 0,7956 + j0,1837 |
= 6,5684e j( 47,8°+360°n ), |
|
||||||||||||
1 − 0,7956 − j0,1837 |
|
|
|
|
|
|
|
|
||||||
где n – целое число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как e2γl = e2αl e j2βl , |
то e2αl |
|
– модуль комплексного числа, а |
|||||||||||
2βl −его аргумент; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2αl = 6,5684 ; α = ln6,5684 |
=1,882 |
= 4,7057мНп км; |
|
|||||||||||
|
|
|
|
|
2l |
|
400 |
|
|
|
|
|
||
2βl = 47,8°+ 360°n = ( 0,829 + 2πn ) рад; |
|
|||||||||||||
|
|
β = |
0,829 + 2πn . |
|
|
|
|
|
||||||
|
|
|
|
|
|
2l |
|
|
|
|
|
|
|
|
Чтобы найти число n, определим приближенно длину волны: |
|
|||||||||||||
|
|
|
с |
|
3 105 |
|
|
|
|
|
|
|
||
|
λ = |
|
|
|
= |
|
=375км . |
|
|
|
||||
|
|
f |
800 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
На расстоянии, равном длине волны, фаза изменяется наπ радиан2 |
. |
|||||||||||||
Поэтому на расстоянии 2l длина волны λ укладывается следующее число раз:
n′ = 2λl = 375400 =1,067 .
Принимаем целое число n = 1 < n′. Отсюда
0,829 + 2π
β = рад км=.0,01778
2l
Коэффициент распространения
γ = α+ jβ = (4,7057+ j17,78) км10.−3 =18,38 10−3 ej75,17° 1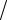
Задача2
Теоретические основы электротехники. Практикум |
-329- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Определить ток в начале однородной линии в режиме холостого хода,
если линия |
длиной 200 км с параметрами Z c = 400e− j5° Ом и |
|
γ = 0,002eкмj80° 1 |
подключена к генератору с напряжением U |
=10 кВ. |
|
1 |
|
Решение
Входное сопротивление линии в режиме холостого хода
Z хх = Z сcthγl .
Определяем
cthγl = |
chγl |
= |
eγl |
+ e−γl |
; |
|
shγl |
eγl |
− e−γl |
||||
|
|
|
γ = α+ jβ = 0,002ej80° = (0,348км + j1,97) 10−3 1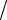
.
γl = 0,0695+ j0,394 (βl в радианах);
eγl = e0,0695 e j0,394 =1,072e j0,394° = 0.99 + j0,411; e−γl = e−0,0695e− j0,394 = 0,933e− j0,394° = 0,862 − j0,358 ;
cthγl = |
1,852 + j0,053 = 2,377e− j78,9°. |
|||
|
0,128 + j0,769 |
|||
Тогда |
|
|
|
|
Z хх = 400e− j5° 2,377e− j78,9° =950,7e− j83,9° Ом. |
||||
Ток в начале линии |
|
|
|
|
I |
|
= |
U1 |
=10,52e j83,9° А. |
|
|
|||
1хх |
|
Z хх |
||
Задача3
В однородной линии задачи 2 найти ток в начале линии в режиме короткого замыкания нагрузки.
Теоретические основы электротехники. Практикум |
-330- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Решение
Входное сопротивление в режиме короткого замыкания
Z кз = Z сthγl = |
Z c |
= |
|
400e− j5° |
=168,28e |
j73,9° |
Ом. |
|||
cthγl |
2,377e− j78,9° |
|
||||||||
|
|
|
|
|
|
|
|
|||
Ток Iкз = |
U1 |
= |
10000 |
|
|
= 59,45e− j73,9° А. |
|
|
||
|
168,28e j73,9° |
|
|
|||||||
|
Zкз |
|
|
|
|
|||||
Задача4
Определить входное сопротивление короткозамкнутой на конце линии
без потерь с параметрами |
L = 0,2мГн км |
и C = 5 10Ф−9 км |
|
при длине |
||||||||||||||||
|
|
1 |
|
|
= 1 λ. |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
||
l |
= |
λ и l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
8 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
||||||
|
|
|
Входное сопротивление короткозамкнутой линии без потерь |
|||||||||||||||||
|
|
|
|
|
|
|
|
Z кз = jZ ctgβl . |
|
|
|
|
||||||||
|
|
|
Волновое сопротивление |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z c = |
|
|
L0 |
|
= 200 Ом. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
C0 |
|
|
π |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
1 λ = |
π , |
|
|
||
|
|
|
Длина волны λ = |
2π |
, отсюда βl |
|
= |
|
tgβl = tg |
=1. |
||||||||||
|
|
|
|
|
|
4 |
||||||||||||||
|
|
|
|
|
|
β |
|
1 |
|
|
λ |
8 |
4 |
1 |
|
|||||
Тогда Zкз1 = j200 Ом, следовательно, имеет индуктивный характер.
Если l2 = λ3 , то βl2 = 23 π, tg 23 π = −1,732 .
Отсюда Z кз2 = − j346 Ом, т. е. имеет емкостный характер.
Задача5
Однородная линия без потерь с параметрами задачи 4 находится в режиме холостого хода. Определить, при какой наименьшей длине линия будет эквивалентна идеальному конденсатору емкостью С = 20 мкФ при
частоте ω =108 с−1.
Теоретические основы электротехники. Практикум |
-331- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Решение
Входное сопротивление
Z хх = − jZ cctgβx .
Волновое |
сопротивление |
Z c = 200 Ом, коэффициент фазы |
||||||||
β = ω |
|
|
= 3,16 |
рад , Z |
|
= − j |
1 |
|
= − j500 Ом. |
|
L C |
0 |
вх |
||||||||
|
||||||||||
0 |
|
м |
|
Сω |
|
|||||
|
|
|
|
|
|
|
||||
После подстановки получим
− j500 = − j200ctgβx ;
ctgβx = 2,5 ; βxmin = 0,38 рад;
X min = 0316,,38 = 0,12 м.
Следующие задачи решите самостоятельно.
Задача6
Определить, при какой наименьшей длине линия задачи 5 будет эквивалентна индуктивному элементу с индуктивностью L = 2 мкГн.
Ответ: X min = 0,745 м.
Задача7
Определить входное сопротивление линии без потерь длиной l = 100 м, если Z c = 200 Ом; Z н =100 Ом и β = 22,9 10−м3 .1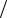
Ответ: Z вх = 212e− j27°Ом.
Задача8
Нагрузкой линии с параметрами предыдущей задачи служит идеальная индуктивная катушка сопротивлением Z н = j600 Ом. Определить
минимальное расстояние от конца линии, при котором входное сопротивление равно нулю.
Ответ: X min = 86,2 м.
Теоретические основы электротехники. Практикум |
-332- |
ГЛАВА 9. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Задача9
Линия без потерь длиной l = 100 км соединяет генератор с активной
нагрузкой |
сопротивлением Rн = 600 Ом. |
Нагрузка потребляет мощность |
P = 50 Вт. |
При частоте 106 Гц линия |
имеет волновое сопротивление |
2 |
|
|
400 Ом. Определить токи и напряжения в начале и в конце линии.
Ответ: I2 = 0,29 А; U2 =174 В; I1 = 0,4 А; U1 =132 В.
Задача10
Определить, на каком расстоянии должна быть закорочена линия без потерь, чтобы она была эквивалентна индуктивному элементу с L =10−5 Гн, еслиZ c =500 Ом, λ = 60 м, υф =3 10км5 с.
Ответ: l = 5,36 м.
Теоретические основы электротехники. Практикум |
-333- |