Контрольные задания

Выполнить необходимые расчёты для построения аппроксимирующей функции вида

,

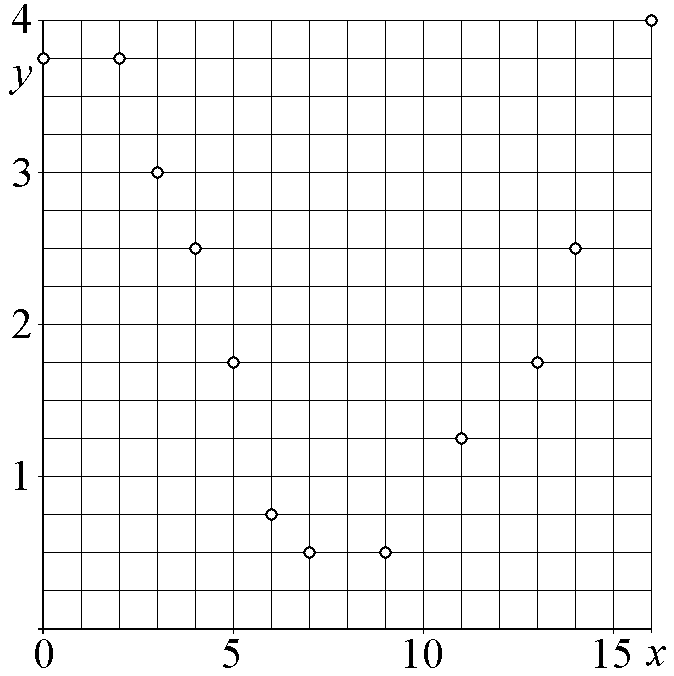
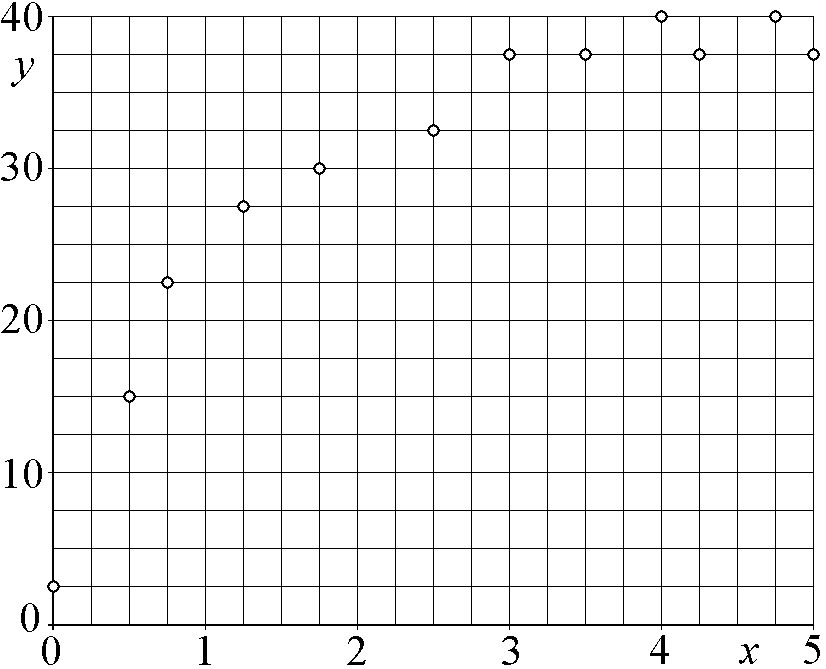
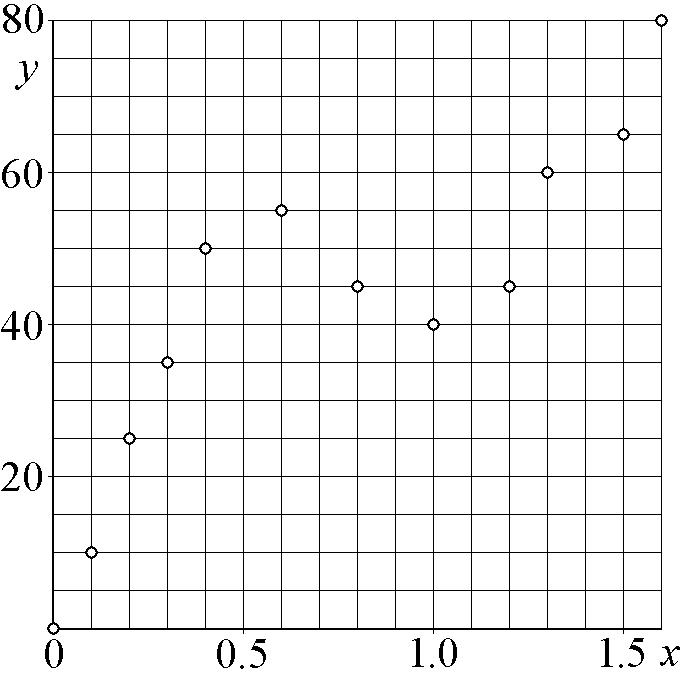
которая описывает экспериментальные данные, приведённые на графиках в количестве 12-ти точек (см. рис.5–14). Для построения аппроксимирующей функции выбрать три базисные функции из четырёх, заданных в таблице 1. Для этого перебрать все возможные варианты формирования аппроксимирующей функции и обосновать свой выбор лучшего варианта. Построить график аппроксимирующей функции вместе с экспериментальными точками. Записать аппроксимирующую функцию с найденными коэффициентами.

Рис.5.	Рис.6.
Рис.7.	Рис.8.

Рис.9.	Рис.10.
Рис.11.	Рис.12.
Рис.13.	Рис.14.

Таблица 1. Варианты базисных функций ₁(x), ₂(x), ₃(x) и ₄(x).

Варианты 1–3 (Рис.5)		Варианты 16–18 (Рис.10)
1
2
3
Варианты 4–6 (Рис.6)		Варианты 19–21 (Рис.11)
4
5
6
Варианты 7–9 (Рис.7)		Варианты 22–24 (Рис.12)
7
8
9
Варианты 10–12 (Рис.8)		Варианты 25–27 (Рис.13)
10
11
12
Варианты 13–15 (Рис.9)		Варианты 28–30 (Рис.14)
13
14
15

6. Решение задачи коши для обыкновенных дифференциальных уравнений 1-го порядка Справочная информация

Обыкновенное дифференциальное уравнение 1-го порядка

с вязывает независимую переменную x, искомую функцию y и её производную. Решение дифференциального уравнения заключается в отыскании функции y = y(x), обращающей это уравнение в тождество на конечном или бесконечном интервале (a, b). Различают общее и частные решения дифференциального уравнения. Общее решение уравнения имеет вид

y = y(x, C),

г

Рис.1.

де C – произвольная постоянная интегрирования. Его графическим отображением является семейство кривых (см. рис.1), называемых интегральными. Каждая интегральная кривая является отображением частного решения, соответствующего своему значению постоянной C. Для выделения частного решения из множества кривых общего решения необходимо задать начальное условие

.

Такая постановка задачи отыскания решения дифференциальных уравнений называется задачей Коши (A.L.Cauchy, 1789–1857). Для существования единственного решения задачи Коши необходимо и достаточно существование и ограниченность правой части дифференциального уравнения f(x, y) и её частной производной f(x, y)/y в некоторой окрестности начальной точки (x₀, y₀).

Для численного решения задачи Коши существует множество методов, которые условно делятся на две группы: одношаговые и многошаговые. Все эти методы позволяют получить искомое решение дифференциального уравнения в виде таблично заданной функции, в т ой или иной мере согласую­щееся с истинным частным решением (см. рис.2). Эти группы методов различаются объёмом информации, которая используется для вычисления координат очередной точки табличной функции. Одношаговые методы используют значения функции и

Рис.2.

её производной только в одной предыдущей точке, в то время как многошаговые – в нескольких. К одношаговым методам решения задачи Коши относятся метод Эйлера, усовершенствованный метод Эйлера, методы Рунге–Кутта, Кутта–Мерсона и другие.

Метод Эйлера (L.Euler, 1768)

Он является старейшим методом решения задачи Коши и заключается в последовательном применении следующих формул

,

,

,

г

Рис.3.

еометрическая интерпре­тация которых при k = 0 представлена на рис.3. В точке (x₀, y₀) вычисляется значение производной dy/dx через f(x, y), которое определяет тангенс угла наклона касательной к графику неизвестного точного решения задачи Коши. Следующая точка численного решения определяется как точка на этой касательной с абсциссой x₁ = x₀+ h. В компактном виде для k = 0, 1, 2,… эти соотношения записываются следующим образом

, .

Метод Эйлера относится к методам первого порядка точности, поскольку его решение совпадает с истинным только в том случае, когда последнее является линейной функцией y = a₁+ a₂x. Его абсолютная погрешность ε_абс(x_k+1, h) на каждом шаге пропорциональна величине h². Это обусловлено тем, что в качестве направления, определяющего положение следующей точки численного решения, используется касательная в левой точке каждого отрезка [x_k, x_k+1]. На рис.3 видно, что для получения более точного численного решения недостаточно знания параметров функции в единственной левой точке отрезка [x_k, x_k+1]. Требуется собрать дополнительную информацию о её поведении на отрезке интегрирования для отыскания решения при x = x_k+1 с меньшей погрешностью. Для этого можно использовать некоторые промежуточные направления, определяемые касательными к графику неизвестного точного решения в характерных точках рассматриваемого отрезка (крайние точки, середина отрезка и т.д.).