Контрольные задания

По номеру своего варианта вычислить один из приведённых ниже определённых интегралов с использованием формулы трапеций и сделать оценку погрешности выполненных вычислений.

1. . 2. . 3. . 4. .

5. . 6. . 7. .

8. . 9. . 10. . 11. .

12. . 13. . 14. .

15. . 16. . 17. . 18. .

19. . 20. . 21. .

22. . 23. . 24. . 25. .

26. . 27. . 28. .

29. . 30. .

2. Решение нелинейных уравнений Справочная информация

К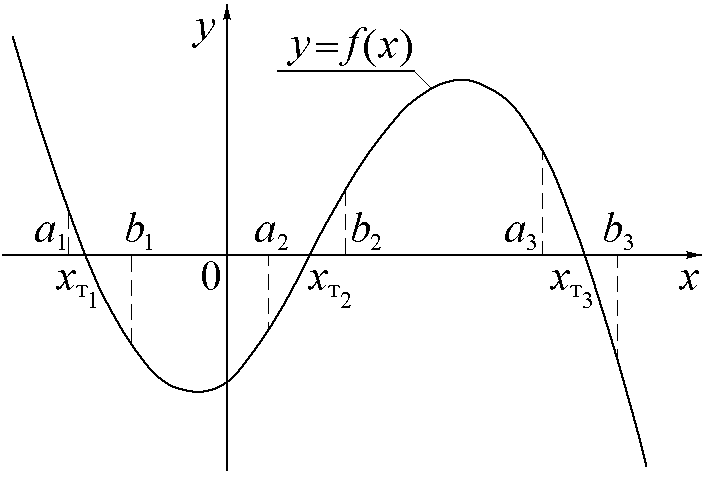 ак известно, далеко не всякое алгебраическое уравнение

может быть решено аналитически. Это относится к большинству трансцендентных уравнений и к алгебраическим уравнениям выше четвёртого порядка. Однако точное решение уравнений на практике часто и не требуется. Чтобы считать задачу решённой, достаточно бывает отыскать значения корней с требуемой степенью точности. Для получения таких решений разработаны численные методы.

Р

Рис.1.

ешение нелинейных уравнений осу­­­ществляется в два этапа. На первом этапе производится отделение корней, то есть поиск достаточно малых отрезков локализации, каждый из которых содержит единственный корень уравнения и на каждом из которых функция f(x) монотонна вместе со своей первой производной. Для этого используется график функции y = f(x), точки пересечения которого с осью абсцисс являются корнями исходного уравнения. Случай, когда корнем уравнения является точка касания графика и оси абсцисс, здесь не рассматривается. Это позволяет выделить отрезки [a, b], содержащие только один корень (см. рис.1). При этом для непрерывной функции f(x) будет выполняться неравенство

f(a) f(b) < 0.

Процесс отделения корней может быть проиллюстрирован на примере уравнения x³ – 7.3x² + 16.8x – 12.2 = 0, для которого корни ищутся на отрезке [0, 3]. Сначала выполняется процесс табулирования функции f(x) = x³ – 7.3x² + 16.8x – 12.2, а затем, используя полученные результаты, строится диаграмма типа «гладкие графики» (см. рис.2). Как видно из графика функции, на этом этапе можно выделить два отрезка локализации корней [1.5, 1.6] и [2.2, 2.4].

На втором этапе внутри выделенных отрезков вычисляются значения каждого из корней уравнения с заданной точностью. Для этого используются два основных итерационных подхода: последователь-

Рис.2.

ное уточнение первоначального приближения значения корня, взятого из выделенного отрезка, и сужение выделенного отрезка, содержащего корень.

Метод половинного деления (метод бисекций)

А

Рис.3.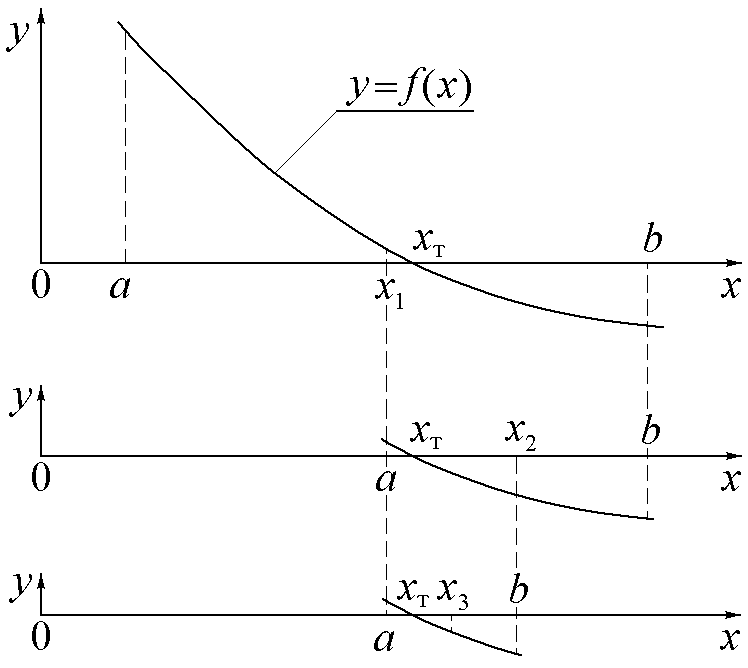

лгоритм метода иллюстрируется на рис.3. Отрезок локализации [a, b] корня делится пополам x₁= (a + b)/2 и в полученной точке вычисляется значение функции. Если f(x₁) = 0, то корень найден и расчёты прекращают. В противном случае из двух отрезков [a, x₁] и [x₁, b] выбирают тот, который содержит корень уравнения. На концах искомого отрезка функция f(x) должна иметь значения разного знака. Для это­го проверяется условие f(a) f(x₁) < 0. При его выполнении в качестве нового отрезка принимается отрезок [a, x₁], в противном случае – [x₁, b]. Процесс вычисления значения корня продолжается до тех пор, пока не будет выполнено требование к точности его определения. В данном случае оценка абсолютной погрешности определения корня

совпадает с длиной отрезка его последней локализации. В свою очередь относительная погрешность вычисляется как

.

При этом за значение корня принимается либо одна из границ суженного отрезка [a, b], либо его середина.

Алгоритм метода может быть проиллюстрирован на рассмотренном выше примере уточнения корня уравнения

x³ – 7.3x² + 16.8x – 12.2 = 0.

В качестве отрезка локализации выбирается отрезок [1.5, 1.6], содержащий первый корень уравнения (см. рис.2). На первом шаге уточнения корня вычисляются значения функции на границах выбранного отрезка

f(1.5) = 1.5³– 7.3·1.5²+ 16.8·1.5 – 12.2 = –0.05,

f(1.6) = 1.6³– 7.3·1.6²+ 16.8·1.6 – 12.2 = 0.088.

Затем в середине отрезка x₁ = 1.55 также вычисляется значение функции

f(1.55) = 1.55³– 7.3·1.55²+ 16.8·1.55 – 12.2 = 0.0256.

Так как эта точка не соответствует корню уравнения, то определяется новый отрезок его локализации. Для этого проверяется знак произведения значений функции на левой границы отрезка локализации корня и в его центре f(1.5)·f(x₁). Из расчётов видно, что это произведение меньше нуля, значит в качестве нового отрезка локализации корня должен приниматься отрезок [1.5, 1.55].

Для выполнения второго шага значения функции на границах нового отрезка локализации считать не нужно, они уже известны

f(1.5) = –0.05, f(1.55) = 0.0256.

Достаточно вычислить её значение в середине нового отрезка локализации корня x₂= 1.525

f(1.525) = 1.525³– 7.3·1.525²+ 16.8·1.525 – 12.2 = –0.0105.

Так как произведение f(1.5) f(x₂) больше нуля, то в качестве нового отрезка локализации принимается [1.525, 1.55]. Аналогично выполняются шаги c третьего по седьмой, дающие следующие значения приближения корня

x₃ = 1.5375 – центр отрезка [1.525, 1.55],

x₄ = 1.53125 – центр отрезка [1.525, 1.5375],

x₅ = 1.53438 – центр отрезка [1.53125, 1.5375],

x₆ = 1.53281 – центр отрезка [1.53125, 1.53438],

x₇ = 1.53203 – центр отрезка [1.53125, 1.53281].

Значение относительной погрешности вычисления приближения x₇= 1.53203 корня уравнения будет определяться по формуле

.

Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью ε_отн = 0.001, то уточнение значения корня можно прекратить.

При реализации метода расчётная таблица может быть составлена в следующем виде:

i	ai	bi	f(ai)		f(xi)
1	a1	b1	f(a1)	x1	f(x1)
2	Если f(a1)f(x1)<0, то a2 = a1, иначе a2 = x1.	Если f(a1)f(x1) 0, то b2 = b1, иначе b2 = x1.	f(a2)	x2	f(x2)
…	….………	…….……	……	…..	……	…….

Ниже на рис.4 представлены результаты расчётов в программе Excel.

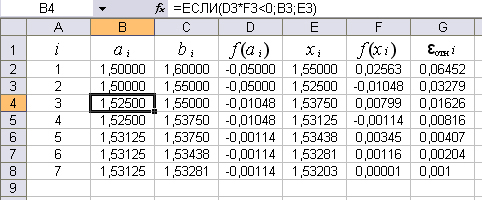
Рис.4.

Метод Ньютона (I.Newton, 1669, Mr.Raphson, 1720)

В данном методе каждое новое приближение к значению корня уравнения f(x) = 0 ищется по следующей итерационной схеме

,

,

………………….

,

………………….

где x₀ – первоначальное приближенное значение корня, взятое с отрезка [a, b] локализации точного решения уравнения.

Если последовательность значений x_k (k = 0, 1, 2,...) сходится к точному значению корня x_т, то абсолютная погрешность значения корня на k-ом шаге (x_k) определяется выражением

, ,

где

, , , .

Может случиться так, что последовательность приближённых значений x_k (k = 0, 1, 2, ...) искомого корня не имеет предела. В этом случае метод расходится, и описанная итерационная схема не может быть применена для решения уравнения. Анализ выражения для ε_абс позволяет сформулировать условие сходимости итераций. Очевидно, для того, чтобы погрешность ε_абс при стремлении k к бесконечности стремилась к нулю и итерации сходились к точному решению, надо обеспечить выполнение следующего неравенства

.

Приведённые формулы для оценки погрешностей и условия сходимости итераций предполагают знание точного решения уравнения x_т и решение дополнительной задачи поиска минимума модуля первой производной функции f(x) и максимума модуля её второй производной на отрезке локализации корня [a, b]. В связи с этим на практике условие сходимости используется в форме

,

где

, ,

а при его выполнении для определения погрешности приближённого решения применяют более грубую её оценку в виде

,

где

, .

Графическая интерпретация работы метода Ньютона пред­ставлена на рис.5. Из точки на кривой y = f(x), имеющей абсциссу x₀, проводитс я касательная до пересечения с осью 0x. Абсцисса точки пересечения принимается за новое приближение значения x₁ корня уравнения f(x) = 0. В случае сходимости последовательности вычисляемых значений x₀, x₁,…, x_k,… процесс продолжается до тех пор, пока не выполнится условие его окончания.

Р

Рис.5.

ассмотрим работу метода Ньютона на примере поиска приближённого значения первого корня уравнения

x³ – 7.3x² + 16.8x – 12.2 = 0,

расположенного на отрезке [1.5, 1.6] (см. рис.2) и оценки погрешности его определения.

Следуя итерационной схеме метода Ньютона, в качестве нулевого приближения искомого корня можно взять x₀ = 1.5 и вычислить первое приближение корня следующим образом

,

где

f(x₀) = f(1.5) = 1.5³ – 7.3·1.5² + 16.8·1.5 – 12.2 = –0.05,

= 3·1.5² – 14.6·1.5+16.8 = 1.65,

Отсюда получается значение корня в первом приближении

.

Вторая итерация:

f(x₁)= 1.5303³ – 7.3·1.5303² + 16.8·1.5303 – 12.2 = –0.00254,

= 3·1.5303² – 14.6·1.5303 + 16.8 = 1.48306,

.

Третья итерация:

f(x₂)= 1.532018³ – 7.3·1.532018² + 16.8·1.532018 – 12.2 = –8·10 ^–6,

= 3·1.532018² – 14.6·1.532018 + 16.8 = 1.47378,

.

Оценку относительной погрешности полученного приближённого решения можно найти по формуле

,

откуда

.

Выполненные вычисления без определения истинного значения относительной погрешности могут быть сведены в таблицу:

i	xi
0	x0
1	x1
…	…..	…………	…..

При реализации в программе Excel эта расчётная таблица метода Ньютона может быть представлена образом, приведённом ниже на рис.6 вместе с результатами расчетов.

Рис.6.