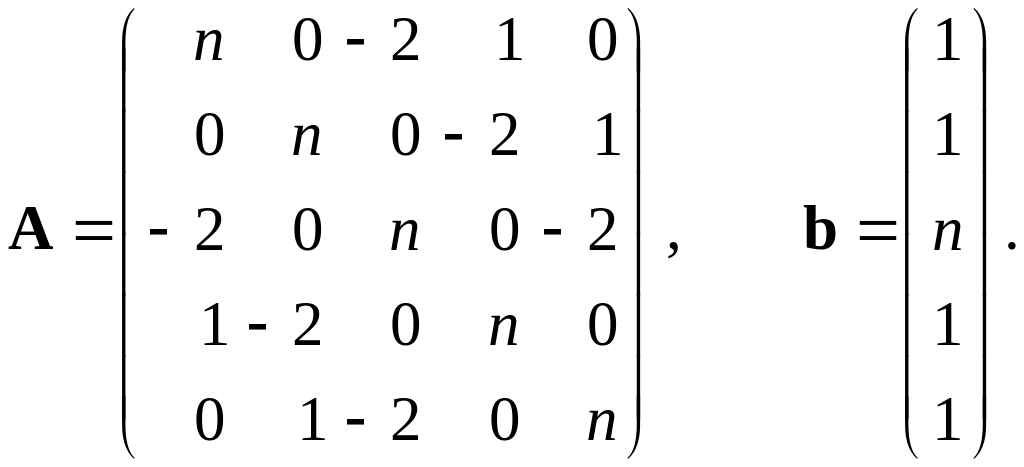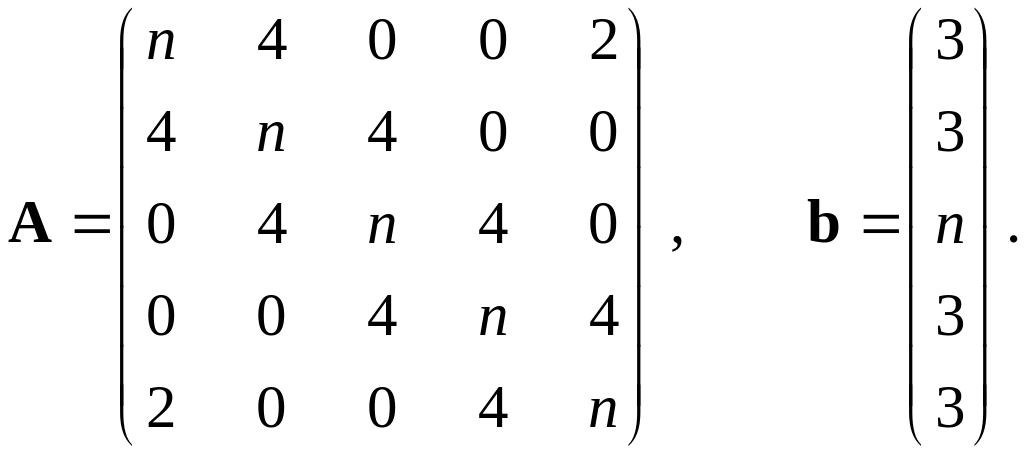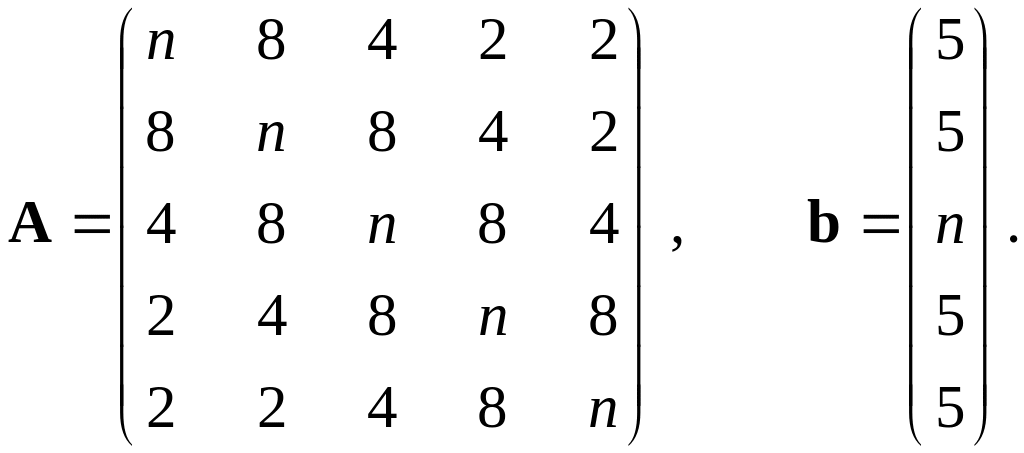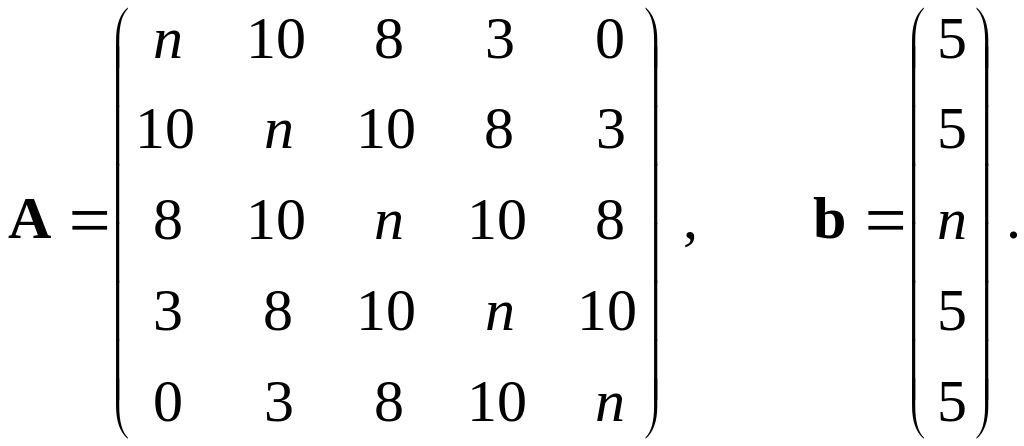Контрольные задания

Методом Гаусса с выбором главного элемента по столбцу найти решение системы линейных алгебраических уравнений . Оценить относительную погрешность полученного решения. Матрицу А и вектор b взять по номеру своего варианта, заменяя параметр n этим номером.

1–5.
6–10.

11–15.
16–20.
21–25.
26–30.

4. Интерполяция таблично заданных функций Справочная информация

Интерполяцией называется представление функции, значения которой заданы в виде таблицы, некоторой другой функцией, которая имеет аналитическое описание и которая совпадает с исходной при табличных значениях аргумента.

Простейшая задача, приводящая к интерполяции функций, заключается в следующем. В дискретные моменты времени x₁, x₂,..., x_n измеряется значение некоторой физической величины y, то есть наблюдается зависимость функции y от аргумента x, и строится таблица

x	x1	x2	...	xn
y	y1	y2	...	yn

П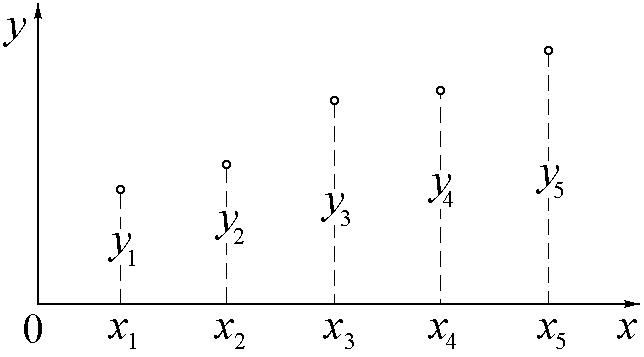 о этой таблице требуется восстановить значения функции при любых других значениях аргумента x из отрезка [x₁, x_n] или подобрать аналитическое выражение для приближающей функции y(x) достаточно простого вида, значения которой совпадали бы с заданными в таблице

.

Г

Рис.1.

еометрический смысл задачи состоит в том, что через точки, которыми отображаются табличные значения аргумента и функции на поле декартовой системы координат x0y, как это показано на рис.1, и которые называются узловыми точками или узлами интерполяции, необходимо провести, по крайней мере, непрерывную линию, подобрав для неё аналитическое описание.

В зависимости от требований, которые накладываются на приближающую функцию, могут применяться различные формы её представления: линейная, квадратичная, кубическая или более высокого порядка. К простейшим из них относятся кусочно-линейная интерполяция, интерполяция кубическим сплайном и интерполяция многочленами, в частности, многочленом Лагранжа и другие.

Интерполяция многочленами

В общем виде задача интерполяции многочленами формулируется следующим образом. Пусть на отрезке [x₁, x_n] таблично задана функция абсциссами x₁, x₂,..., x_n и ординатами y₁, y₂,..., y_n своих узловых точек. Требуется построить степенной полином вида

,

значения которого в точках x₁, x₂,..., x_n совпадает со значениями этой табличной функции

Такой полином всегда существует и оказывается единственным. Для вычисления коэффициентов этого полинома пользуются условиями равенства его значений и значений таблично заданной функции в узлах интерполяции. Это даёт систему из n линейного алгебраического уравнения относительно коэффициентов a₀, a₁,..., a_n вида

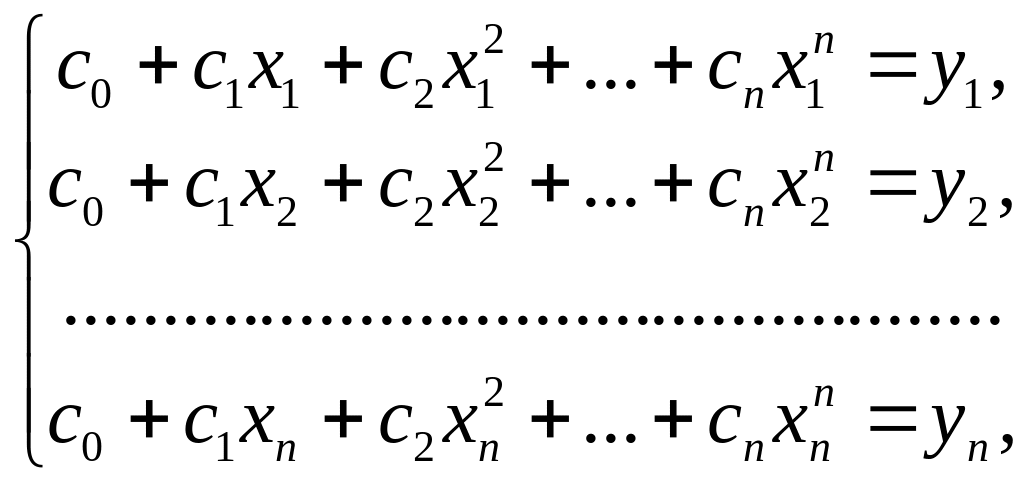
которая в матричной форме записывается следующим образом

и которая может быть разрешена любым из известных методов решения систем линейных алгебраических уравнений.

Использование такого подхода имеет ряд недостатков. Во-первых, с увеличением количества n узлов интерполяции пропорционально возрастает и степень системы линейных алгебраических уравнений, что приводит к усложнению ее решения. Во-вторых, с ростом n возрастает вероятность «биения» функции между узлами интерполяции за счёт членов полинома с высокими степенями.

x	0	1	2	3
y	2	0.5	1	4

Рассмотрим применение этого подхода на примере кусочно-линейной интерполяции таблично заданной функ­ции и поиска её значения при аргументе х = 1.6.

Для решения задачи строится полином 3-го порядка

,

коэффициенты которого есть решение следующей системы линейных алгебраических уравнений

В матричной форме эта система имеет вид

.

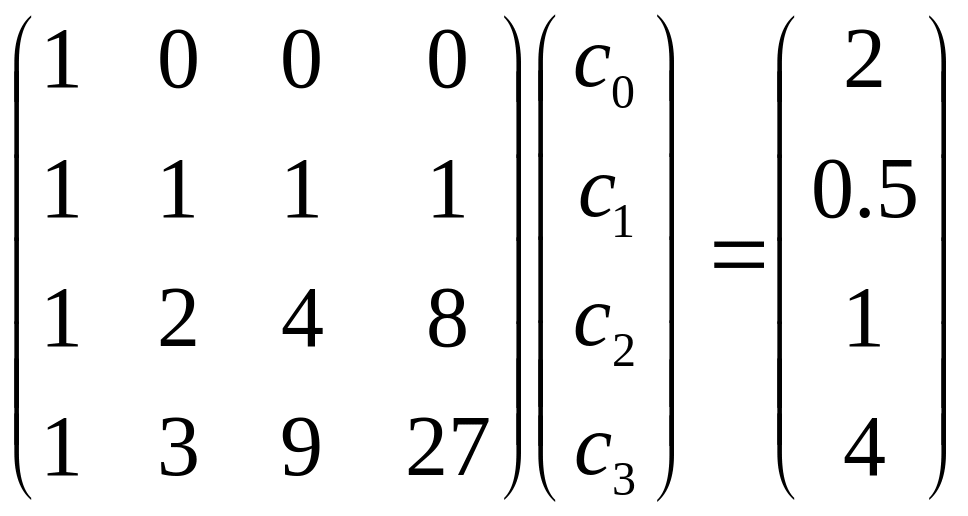Её решение получается любым доступным методом, например методом Гаусса

.

Таким образом, табличная функция в случае интерполяции полиномом представляется в виде

.

Её значение в заданной точке x = 1.6 будет

.

Ниже на рис.2 представлен фрагмент рабочей книги Excel с реализацией интерполяции полиномом. При построении графика приближающей функции аргумент х изменяется с шагом 0.2, а значения функции вычисляются по общей формуле, адаптированной под конкретные значения из диапазона изменения аргумента.

Многочлен Лагранжа (J.L.Lagrange, 1795)

Представляет собой случай полиномиального представления приближающей функции, когда она ищется в виде линейной комбинации базисных функций _k(x), которые должны быть определены для всего отрезка интерполяции [x₁, x_n], линейно независимы, и их количество должно быть равно числу узлов таблично заданной функции

.

Коэффициенты с₁, с₂, ..., с_n определяются исходя из условий ра-

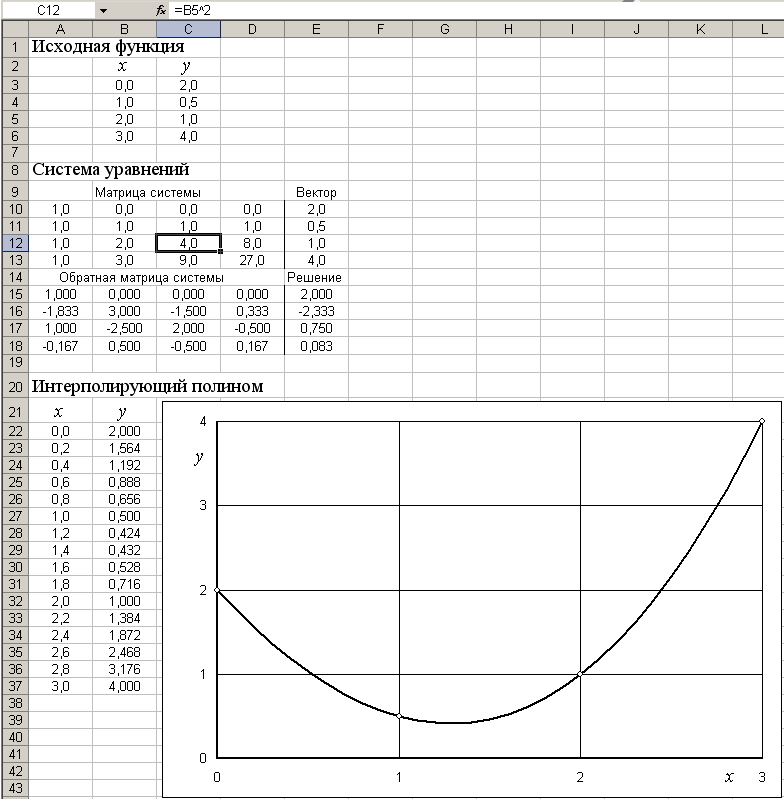
Рис 2.

венства значений приближающей и исходной функций при табличных значениях аргумента, что сводит задачу к системе n линейных алгебраических уравнений относительно них, а в качестве функций _k(x) используются полиномы (n–1) степени

,

которые для пяти узловых точек записываются в виде

,

,

,

,

.

Для каждого полинома характерно то, что для всех значений x_i в узловых точках он принимает нулевые значения, кроме k-ой, где его значение равно единице. Графики этих полиномов пред­ставлены на рис.3.

При таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции, а сама она приобретает характерный для многочлена Лагранжа вид

.

Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.4.

Рассмотрим работу метода на приведённом выше примере интерполяции таблично заданной по 4-м точкам функции. Сначала строятся четыре базовых полинома:

,

,

,

.

Рис.3.

Рис.4.

Они позволяют записать интерполирующий многочлен Лагранжа в виде

.

Для аргумента x = 1.6 многочлен Лагранжа даёт

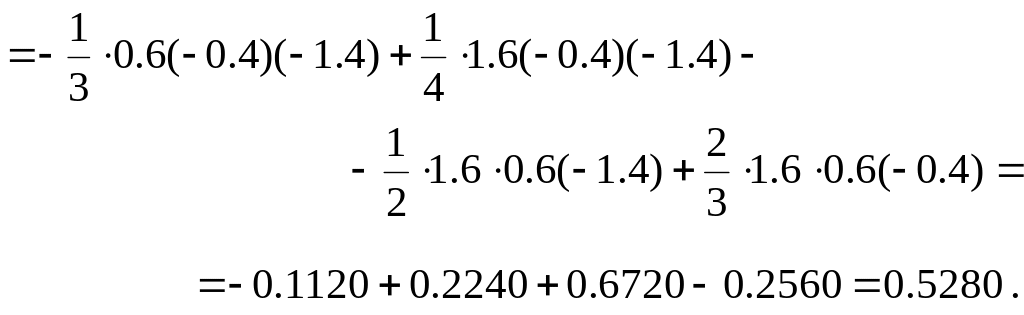
Ниже на рис.5 представлен фрагмент рабочей книги Excel с реализацией интерполяции с помощью многочлена Лагранжа. Как видно из рисунка для аргумента x = 1.6 многочлен Лагранжа дал значение 0.528.

Для контроля правильности вычислений многочлена Лагранжа полезно строить графики базовых полиномов. Для рассматриваемого примера они приведены на рис.6.