Контрольные задания
Получить решение задачи Коши на указанном отрезке с использованием метода из числа рассматриваемых в лабораторной работе. Оценить относительную погрешность полученного решения.
1.
.
2.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
15.
.
16.
.
17.
.
18.
.
19.
.
20.
.
21.
.
22.
.
23.
.
24.
.
25.
.
26.
.
27.
.
28.
.
29.
.
30.
.
7. Решение задачи коши для нормальных систем обыкновенных дифференциальных уравнений и уравнений высших порядков Справочная информация
Задача Коши для нормальной системы обыкновенных дифференциальных уравнений записывается в виде
или в матричной форме
,
,
где
,
,
.
Система дифференциальных уравнений связывает независимую переменную x, искомые функции y1, y2,..., yn и их первые производные. В данном случае решение задачи Коши заключается в отыскании функций y1 = y1(x), y2 = y2(x),..., yn = yn(x), обращающих каждое уравнение системы в тождество на конечном или бесконечном интервале (a, b) и удовлетворяющих начальным условиям.
Такая форма записи задачи Коши является канонической для систем обыкновенных дифференциальных уравнений. К ней могут быть приведены как любые другие формы представления систем дифференциальных уравнений, разрешённых относительно старших производных, так и дифференциальные уравнения высших порядков. Приведение дифференциальных уравнений высших порядков к нормальной системе дифференциальных уравнений осуществляется по следующей схеме. Если дана задача Коши следующего вида
,
,
то замена переменных
сводит её к нормальной системе дифференциальных уравнений с начальными условиями
образующих задачу Коши.
Для решения такой задачи Коши используются те же методы, что для обыкновенных дифференциальных уравнений 1-го порядка. Это обуславливается тем, что матричная форма записи задачи Коши для нормальной системы полностью совпадает с её формулировкой для этих уравнений. Аналогична для неё и теорема о существовании единственного решения. Единственным отличием здесь является то, что вместо функций y(x) и f(x, y) используются вектор-функции y и f, которые состоят из n функций y1(x), y2(x),..., yn(x) и f1(x, y1,..., yn), f2(x, y1,..., yn),..., fn(x, y1,..., yn), соответственно. При этом расчётные схемы методов и оценки их погрешностей сохраняются.
Метод Эйлера
Соотношения метода Эйлера для нормальной системы в матричной форме имеют вид
,
или в развёрнутой форме
,
где верхний индекс показывает номер шага по аргументу x.
Геометрическая интерпретация работы метода Эйлера решения задачи Коши для нормальной системы идентична его геометрической интерпретации для дифференциальных уравнений 1-го порядка. Однако в данном случае движение осуществляется вдоль некоторой кривой в (n + 1)-мерном пространстве переменных x, y1, y2,..., yn, которая является геометрическим представлением вектор-функции y.
Оценка погрешности метода
Все оценки погрешности, полученные для решений задачи Коши для одного дифференциального уравнения 1-го порядка, остаются справедливыми и для решения систем аналогичных дифференциальных уравнений. В силу этого абсолютная погрешность метода Эйлера на каждом шаге пропорциональна величине h2
.
Здесь
,
где
.
При
вычислении коэффициента Ck+1
в качестве вектор-функции
используется некая промежуточная
функция, кривая которой в (n+1)-мерном
пространстве переменных x,
y1,
y2,...,
yn,
располагается между кривыми приближённого
и неизвестного точного решений.
Абсолютная погрешность вычисления приближённого решения на отрезке интегрирования системы дифференциальных уравнений после n-го шага оценивается следующим образом
,
где m = 2 для метода Эйлера и
.
На практике такое вычисление абсолютных погрешностей решения задачи Коши затруднено. Поэтому, как правило, для вычисления погрешности методов используют апостериорную оценку, базирующуюся на правиле Рунге
,
где y(xk, h) и y(xk, 2h) – приближённые значения вектора решения, вычисленные в точке xk при шагах интегрирования, отличающихся друг от друга в два раза.
В качестве относительной погрешности решения задачи Коши на отрезке [x0, xn], как и в случае одного дифференциального уравнения 1-го порядка, используют интервальную оценку
.
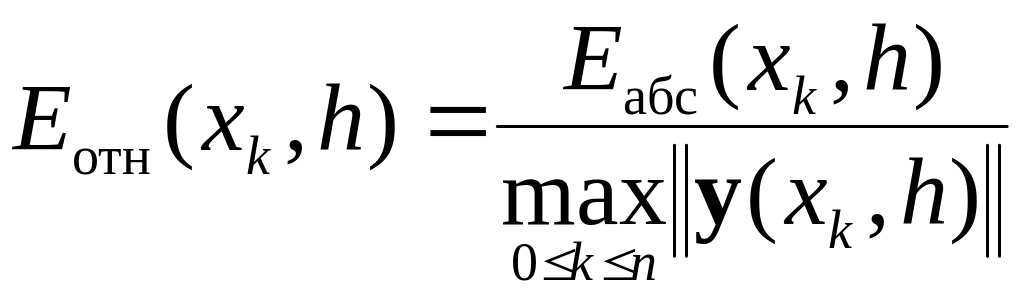Алгоритм метода
Эйлера решения задачи Коши и оценка
погрешности получаемых результатов
может быть проиллюстрирован на примере
решения уравнения
с начальными условиями y(0)
= 0,
на отрезке [0, 0.4] с шагом h
= 0.1.
На первом этапе дифференциальное уравнение 2-го порядка должно быть преобразовано к эквивалентной системе дифференциальных уравнений 1-го порядка. Для этого вводятся следующие обозначения
,
что позволяет записать исходную задачу Коши в виде системы
В соответствии с алгоритмом метода Эйлера расчётная схема решения системы дифференциальных уравнений может быть представлена в виде следующих соотношений
,
Таким образом, процесс решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом
Для получения оценки погрешности решения необходимо повторить проделанные расчёты с удвоенным шагом h = 0.2
Эти результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1
,
,
,
,
,
,
,
,
,
,
.
Возможный вариант реализации метода Эйлера в программе Excel представлен на рис.1. Здесь решена задача Коши, подобная рассмотренной выше. Отличие состоит в том, что отрезок построения решения увеличен до отрезка [0, 2]. Сравнение решений с шагами h = 0.1 и h = 0.05 позволяет оценить погрешность последнего.
Рис.1.