Симплексные таблицы.

При практических расчетах реальных задач удобно использовать симплексный метод реализованный в симплексных таблицах. Рассмотрим алгоритм их составления на примере конкретной задачи, не углубляясь в его подробное обоснование. Вернемся к задаче 1 ( текст задачи см. лекция 29). Найти максимум функции при выполнении следующих условий :

Приведем задачу к каноническому виду, добавив в каждое неравенство системы ограничений по балансовой переменной, указывающей величину остатков сырья соответствующего вида:

Выпишем матрицу и расширенную матрицу этой системы:

Их ранг равен 3, значит система совместна и имеет три базисные переменные. Общий вид таблиц следующий:

С			С1	С2	…	Сq	…	Cn
Базисные переменные	Сбаз	В	А1	А2	…	Аq	…	Аn
			a11	a12	…	a1q	…	a1n
			a21	a22	…	a2q	…	a2n
					…		…
			ai1	ai2	…	aiq	…	ain
					…		…
			am1	am2	…	amq	…	amn
					…		…
					…		…

В первой строке этой таблицы указаны коэффициенты при переменных целевой функции. В столбцы А_j записывают коэффициенты при переменной х_j. В столбец В записывают свободные члены уравнений системы линейных ограничений. В первый столбец симплекс таблицы заносят наименования переменных, которые образуют единичный базис. Если такого базиса нет, то можно выбрать любые переменные в качестве базисных, при этом число базисных переменных равно рангу матрицы системы ограничений. Две последние строки таблицы предназначены для проверки полученного плана на оптимальность. Значения вычисляются как скалярное произведение . Значение целевой функции на данном шаге можно вычислить так: . Оценки переменных вычисляются по формуле .

Заполним первую симплексную таблицу для нашей задачи. В качестве трех базисных переменных выберем переменные х₃ , х₄ , х₅.

Таблица 1.

С			3	9	0	0	0
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5
x3	0	714	6	3	1	0	0
x4	0	910	5	10	0	1	0
x5	0	948	3	12	0	0	1
		0	0	0	0	0	0
			3	9	0	0	0

Проверяем выполнение критерия оптимальности ( формулировку см.выше ). В переложении для применения в симплексных таблицах возможны следующие варианты:

1. Если все оценки не положительны , то найденный план оптимален, решение закончено.

2. Если имеются положительные оценки, например, , для которой все , то целевая функция неограничена сверху на множестве планов и задача не имеет конечного решения.

3. Если столбцов описанных в пункте 2 нет, но имеется положительная оценка, то продолжаем решение, выбирая новый базис.

Для выбора нового базиса выделим наибольшую из положительных оценок. Пусть это будет . Назовем столбец с номером q – разрешающим. В этом столбце для положительных коэффициентов составим отношения , из которых выберем минимальное. Если оно получено в строке с номером p, (т.е. ), то эту строку назовем разрешающей. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент . Новой базисной переменной вместо х_p будет переменная х_q. В нашей задаче наибольшая из положительных оценок «9» находится во втором столбце. Этот столбец будет разрешающим. Найдем разрешающую строку: 714/3=238; 910/10=91; 948/12=79. Минимальное значение – «79», значит третья строка будет разрешающей. Переходим к новой таблице по следующим правилам:

1. Заменим в первом столбце таблицы имя старой базисной переменной, стоящей в p-й строке ( х_p= х₅ ), на имя новой базисной переменной согласно номеру разрешающего столбца ( х_q= х₂ ).

2. В столбцах, соответствующих основным переменным, проставляем нули и единицы: 1 - против «своей» основной переменной, 0 - против «чужой» основной переменной.

3. Все элементы разрешающей строки делим на разрешающий элемент .

4. Далее производим пересчет остальных элементов симплекс-таблицы по методу Гаусса-Жордана. К каждой из остальных строк прибавляем преобразованную разрешающую строку, умноженную на такое число, чтобы в разрешающем столбце получился 0. Эти преобразования в виде формул можно записать так:

Таблица 2.

С			3	9	0	0	0
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5
x3	0	477	21/4	0	1	0	-1/4
x4	0	120	5/2	0	0	1	-5/6
x2	9	79	1/4	1	0	0	1/12
		711	9/4	9	0	0	3/4
			3/4	0	0	0	-3/4

Анализ полученной таблицы 2 показывает, что решение не оптимально. Наибольшая (и единственная) из положительных оценок находится в первом столбце. Он будет разрешающим. Найдем разрешающую строку: 79:(1/4)=316; 477:(21/4)=90.9; 120:(5/2)=48. Минимальное значение – «48», значит вторая строка будет разрешающей. Базисная переменная х₄ меняется на переменную х₁. Переходим к следующей таблице по описанным выше правилам.

Таблица 3.

С			3	9	0	0	0
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5
х3	0	225	0	0	1	-2.1	1.5
х1	3	48	1	0	0	2/5	-1/3
х2	9	67	0	1	0	-0.1	1/6
		747	3	9	0	0.3	0.5
			0	0	0	-0.3	-0.5

Данные этой таблицы указывают на оптимальность полученного решения, согласно которому целевая функция достигает максимального значения 747 при х₁=48, х₂=67, х₃=225, х₄=0, х₅=0.

В случае, если при приведении задачи к каноническому виду не удается сразу получить базис, т.е. среди векторов-столбцов матрицы ограничений нет единичного вектора, содержащего 1 на i-ом месте, то используется М-метод или метод искусственного базиса. В левую часть i-ого уравнения добавляется новая переменная х_j, ( ). Она становится недостающей базисной переменной и вводится в целевую функцию с коэффициентом (-М), где М – очень большое положительное число ( настолько большое, что все алгебраические суммы, в которые М входит с положительным коэффициентом – положительны, а все алгебраические суммы, в которые М входит с отрицательным коэффициентом – отрицательны ). Такие переменные называют искусственными или М-переменными, а построенную задачу М-задачей.

Пример 1: Построить М-задачу: найти максимум функции F=-2x₁-3x₂-4х₃ при ограничениях

Преобразовав неравенства в равенства, получим следующую систему ограничений:

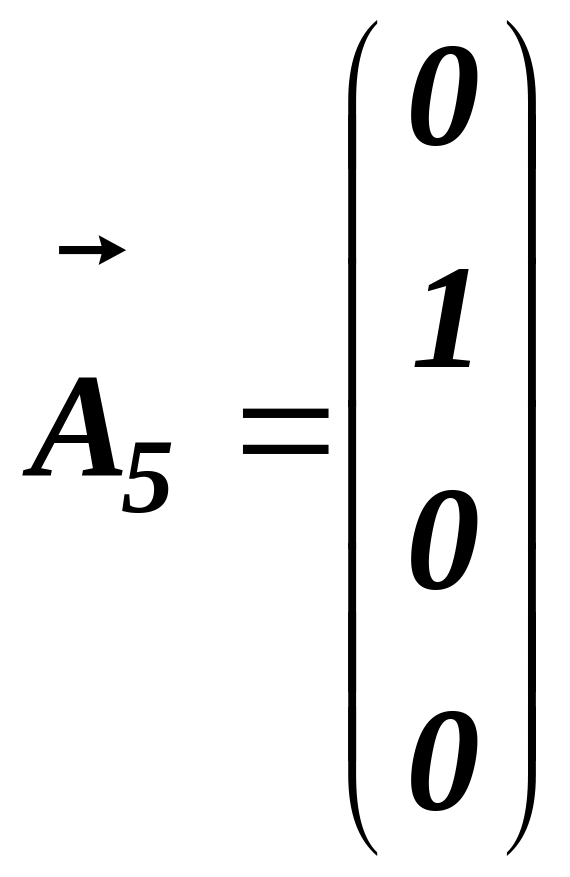В матрице ограничений полученной задачи есть два единичных вектора-столбца: и . Чтобы получить еще два единичных вектора, введем две М-переменные х₇ и х₈ в третье и четвертое уравнения. В целевую функцию х₇ и х₈ вводим с коэффициентом (-М). Окончательно имеем следующую формулировку М-задачи:

найти максимум функции F= -2x₁ - 3x₂ - 4х₃ - Мх₇ - Мх₈ при ограничениях

Решим эту задачу с помощью симплекс-таблиц так же, как решали каноническую задачу линейного программирования. Приведем все тре6уемые симплекс-таблицы без подробных комментариев.

Таблица 1.

С			-2	-3	-4	0	0	0	-М	-М
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5	А6	А7	А8
x4	0	12	2	3	1	1	0	0	0	0
x5	0	14	2	1	2	0	1	0	0	0
x7	-М	4	1	1	0	0	0	0	1	0
x8	-М	2	0	0	1	0	0	-1	0	1
		-6М	-М	-М	-М	0	0	М	-М	-М
			М-2	М-3	М-4	0	0	-М	0	0

Таблица 2.

С			-2	-3	-4	0	0	0	-М	-М
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5	А6	А7	А8
x4	0	4	0	1	1	1	0	0	-2	0
x5	0	6	0	-1	2	0	1	0	-2	0
x1	-2	4	1	1	0	0	0	0	1	0
x8	-М	2	0	0	1	0	0	-1	0	1
		-2М-8	-2	-2	-М	0	0	М	-2	-М
			0	-1	М-4	0	0	-М	-М+2	0

Таблица 3.

С			-2	-3	-4	0	0	0	-М	-М
Базисные переменные	Сбаз	В	А1	А2	А3	А4	А5	А6	А7	А8
x4	0	2	0	1	0	1	0	1	-2	-1
x5	0	2	0	-1	0	0	1	2	-2	-2
x1	-2	4	1	1	0	0	0	0	1	0
x3	-4	2	0	0	1	0	0	-1	0	1
		-16	-2	-2	-4	0	0	4	-2	-4
			0	-1	0	0	0	-4	-М+2	-М+4

Ответ: F( 4,0,2,2,2,….)=16.

Возможен и другой принцип выбора уравнений для введения М-переменных. Они вводятся не сразу после приведения задачи к каноническому виду, а после получения первого базисного решения. Выбираются те уравнения, которые дают отрицательную компоненту в базисном решении и в каждое из них вводится новая неотрицательная искусственная переменная, которая имеет тот же знак, что и свободный член в правой части уравнения. В первой симплекс-таблице все искусственные переменные и обычные добавочные переменные, дающие неотрицательные компоненты базисного решения включаются в число базисных.

Пример 2: Построить М- задачу: найти максимум функции F=x₁+2x₂ при ограничениях:

.

Если мы возьмем в качестве базисных переменных х₁ и х₂, то получим недопустимое базисное решение Х=(0; 0; -1; 3; 5) с одной отрицательной компонентой, получающейся из первого уравнения. Введем в первое уравнение искусственную переменную у₁ с тем же знаком, что и свободный член. Также новую переменную введем в целевую функцию с коэффициентом (-М). Окончательно получим: найти максимум функции F=x₁ + 2x₂ - My₁ при ограничениях:

В обоих случаях дальнейшее решение задачи ничем не отличается от изложенного выше.