Лекция 29

Лекция 29. Математическое программирование: экстремум функции нескольких переменных в замкнутых областях; линейный случай; примеры задач линейного программирования. Геометрический смысл линейных уравнений и неравенств. Экономические задачи, приводящие к системам неравенств, их формализация. Графический метод решения задач линейного программирования.

В 1938-1939 ленинградский математик ( впоследствии акаде­мик, лауреат Ленинской, Государственных и Нобелевской премий ) Л.В.Канторович в результате анализа ряда проблем организации и планирования производства сформулировал новый класс условно-экстремальных задач и предложил методы их решения. Так было положено начало развитию нового раздела математики - линейному программированию. Однако, вследствие научной изоляции СССР, идеи Канторовича и других ученых, занимавшихся этой и близкими ей проблемами, замечены в мире не были. В 5о-х годах ме­тод был "создан" заново американским математиком Данцигом. Название метода прижилось в результате не совсем удачного перевода одной из работ Данцига, т.к. английское "programming" лучше соответствует русскому "планирование".

Линейное программирование - раздел математики, в котором изучаются методы решения задач на отыскание экстремума линейной функции нескольких переменных при наличии ограничений в виде линейных уравнений и неравенств.

1. Примеры задач линейного программирования. Построение их экономико-математических моделей.

1.1. Задача оптимального использования ресурсов. ( первый тип )

Для изготовления различных изделий А и В предприятие использует три вида сырья. На производство единицы изделия А требуется затратить сырья первого вида 6 кг, второго 5 кг, третьего 3 кг. На производство единицы изделия В соответственно: 3, 10 и 12 кг. Производство обеспечено сырьем первого вида в количестве 714 кг, сырьем второго вида в количестве 910 кг и третьего вида - 948 кг. Прибыль от реализации единицы готового изделия А составляет 3 руб., а изделия В - 9 руб. Составить план производства изделий А и В, при котором прибыль от их реализации максимальна. Формализуем условие этой задачи. Пусть - планируемое количество изделий А, - планируемое количество изделий В, тогда затраты сырья первого вида на их производство составят кг, сырья второго вида кг, сырья третьего вида кг, прибыль составит руб. Учитывая ограничения по количеству сырья и естественное требование, что и - неотрицательны, поставленную задачу можно записать так: найти максимум функции при выполнении следующих условий:

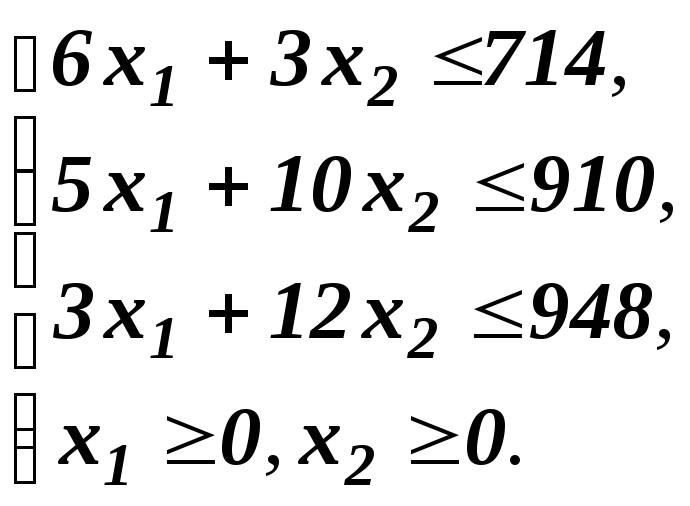
1.2.Задача оптимального использования ресурсов.( второй тип )

На сортировочной станции находятся 136 плацкартных вагонов, вмещающих по 48 пассажиров, 112 купейных на 28 мест и 80 мягких, имеющих 24 места. Можно составлять 2 типа поездов: 1 тип состоит из 10 плацкартных, 4 купейных и 2 мягких вагонов, 2 тип - из 2 плацкартных, 8 купейных и 6 мягких. Сколько поездов того и другого типа надо составить, чтобы число пассажиров было максимальным? Если число поездов 1-го типа х₁, а число поездов 2-го типа х₂, то количество используемых плацкартных вагонов равно 10х₁+2х₂, купейных – 4х₁+8х₂, мягких – 2х₁+6х₂. Число пассажиров в поезде первого типа - 640 человек, в поезде второго типа 464 человека. Следова­тельно, задачу можно записать так: найти максимум функции F=640х₁+464x₂, при условии, что

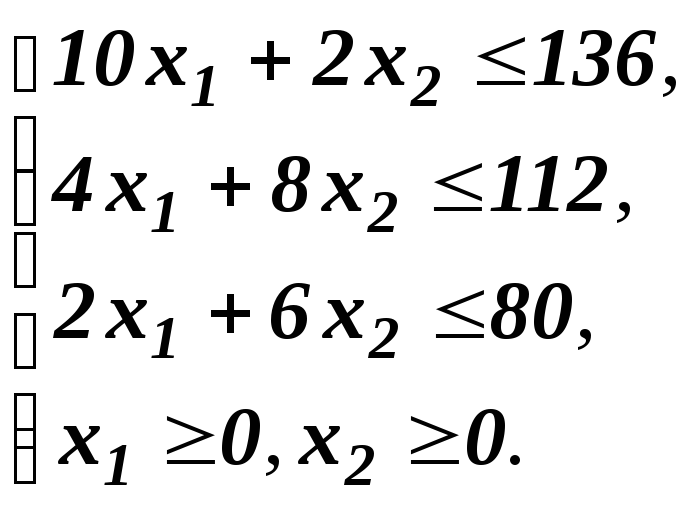
1.3.Задача оптимального раскроя.

В мастерской имеются брусья длиной 1 м. Из них надо выпилить 12 брусков длиной 0.34 м и 25 брусков длиной 0.21 м. Возможны три способа распила.

1 способ: 2 заготовки по 0.34 м и 1 заготовка длиной 0.21 м, в отходы попадает 0.11 м.

2 способ: 1 заготовка по 0.34 м, 3 заготовки длиной 0.21 м, в отхода попадает 0.03 м.

3 способ: 4 заготовки по 0.21 м. в отходы попадает 0.16 м.

Определить, сколько брусьев надо распилить по каждому из возможных вариантов, чтобы общая величина отходов была минимальной. Если x₁ - число брусьев, распиленных первому варианту, х₂ - по второму и х₃ - по третьему, то задачу можно записать следующим образом: найти минимум функции F=0.11х₁+0.03х₂+0.16х₃, при условии, что

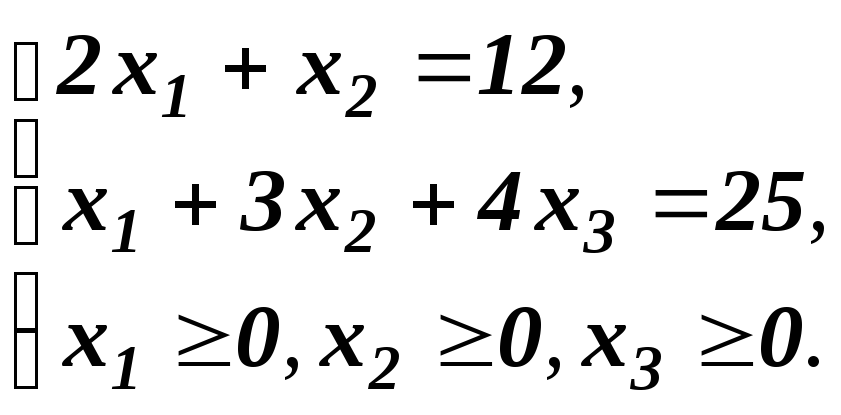
1.4. Задача составления рациона ( задача о диете, задача о смесях).

Имеется два вида корма А и В, содержащие питательные вещества (витамины) S₁,S₂ и S₃. В корме вида А содержится 3 ед. вещества S₁, 1 ед. вещества S₂, 1 ед. вещества S₃. В корме вида В содержится 1,2 и 6 ед. веществ S₁,S₂ и S₃ соответственно. Необходимый минимум питательных веществ S₁,S₂ и S₃ составляет 9,8 и 12 ед. Стоимость 1 кг корма А и В соответственно 4 и 6 руб.

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

Обозначим х₁, х₂ – количество кормов А и В, входящих в дневной рацион. Тогда этот рацион ( 3х₁+х₂ ) ед. питательного вещества S₁, ( х₁+2х₂ ) ед. питательного вещества S₂ и ( х₁+6х₂ ) ед. питательного вещества S₃. Так как содержание питательных веществ в рационе должно быть не менее 9, 8 и 12 ед. соответственно, то получим систему неравенств:

Общая стоимость рациона составит: F=4x₁+6x₂ руб.

Требуется составить такой рацион Х=( х₁,х₂ ), удовлетворяющий указанной системе ограничений, при котором функция F принимает минимальное значение.

1.5.Задача об использовании мощностей (задача о загрузке оборудования).

Предприятию задан план производства продукции по времени и номенклатуре: требуется за время Т выпустить n₁,n₂,…,n_k единиц продукции P₁,P₂,…P_k. Продукция производится на станках S₁,S₂,…S_m. Для каждого станка известны производительность а_ij (т.е. число единиц продукции P_j которое можно произвести на станке S_i) и затраты b_ij на изготовление продукции P_j на станке S_i в единицу времени.

Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.

Обозначим х_ij – время, в течение которого станок S_i будет занят изготовлением продукции P_j (i=1,2,…m;j=1,2,…k).

Так как время работы каждого станка ограничено и не превышает Т, то справедливы неравенства:

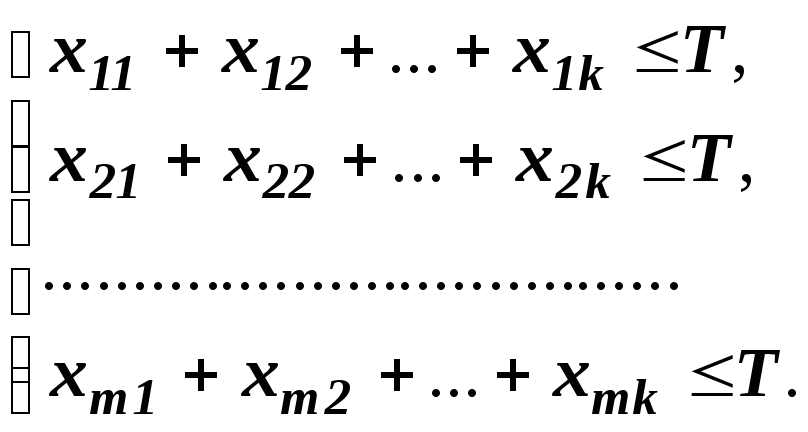
Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства:.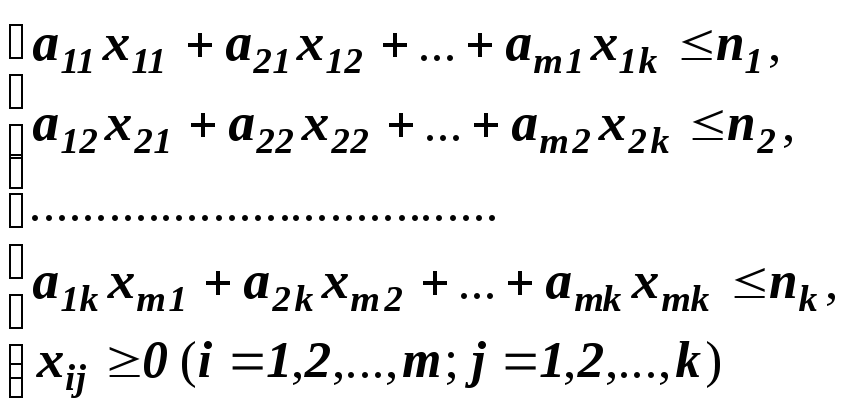

Затраты на производство всей продукции выразятся функцией:

F = b₁₁x₁₁+b₁₂x₁₂+…+b_mkx_mk.

Требуется найти такое решение Х=( х₁₁,х₁₂,…,х_mk ), удовлетворяющее обеим системам ограничений и при котором функция F принимает минимальное значение.