Лекция 29

Лекция 30-31. Симплекс-метод. Аналитический способ. Симплекс-таблицы. М-задачи ( метод искусственного базиса ).

Симплексный метод решения задач линейного программирования.

Как мы уже выяснили в предыдущей лекции, для того, чтобы решить любую задачу линейного программирования достаточно перебрать конечное число допустимых базисных решений системы ограничений и выбрать среди них то, на котором целевая функция принимает оптимальное значение. Геометрически это соответствует перебору всех угловых точек многогранника решений. Такой перебор в конце концов приведет к оптимальному решению, (если оно существует), однако его практическое осуществление весьма проблематично. Дело в том, для реальных задач число допустимых базисных решений может быть очень велико.

Число перебираемых допустимых базисных решений можно сократить, если производить перебор не беспорядочно, а с учетом изменений целевой функции, т.е. добиваясь того, чтобы каждое следующее решение было “лучше” ( или, по крайней мере, не ”хуже” ), чем предыдущее, по значениям целевой функции ( увеличение ее при отыскании максимума F, уменьшении – при отыскании минимума F). Такой перебор позволяет сократить число шагов при отыскании оптимума.

Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирования – симплексного метода.

Симплексный метод, позволяющий решить любую задачу линейного программирования, универсален. В основном он используется для расчетов на компьютерах, но несложные задачи с применением симплексного метода можно решать и вручную.

Для реализации симплексного метода необходимо освоить три основных элемента:

1. способ определения какого-либо первоначального допустимого базисного решения задачи;

2. правило перехода к лучшему ( точнее, не худшему ) решению;

3. критерий проверки оптимальности найденного решения.

Для использования симплексного метода задача линейного программирования должна быть приведена к каноническому виду, т.е. система ограничений должна быть представлена в виде уравнений, а у целевой функции следует находить максимум.

Поясним идею применения симплексного метода на примере задачи 2. Представим эту задачу в канонической форме, добавив новые переменные х₃,х₄ и х₅, которые имеют смысл числа неиспользованных плацкартных, купейных и мягких вагонов: найти максимум F( х₁,х₂,х₃,х₄,х₅ ) = 640х₁ + 464x₂, при условии, что

Исследуем наличие ОДР для этой задачи. Система линейных уравнений совместна, если ранг расширенной матрицы и матрицы системы равны. Выпишем расширенную матрицу системы ( отделив вертикальной чертой элементы матрицы системы от свободных членов уравнений ):

.

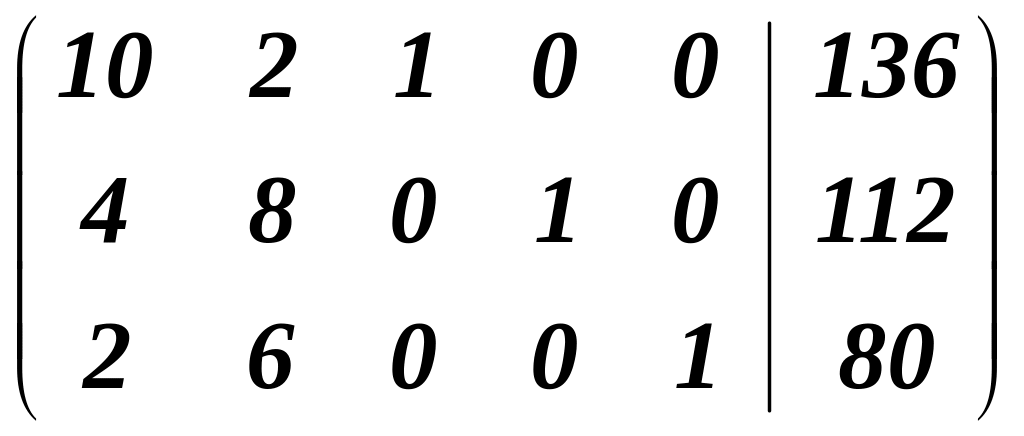Так как и для расширенной матрицы и для матрицы системы можно найти отличные от нуля миноры третьего порядка, то их ранг совпадает и равен 3. Значит система совместна, ОДР существует. Поскольку ранг меньше числа неизвестных, то система имеет бесконечное множество решений, имеющих вид линейных зависимостей трех базисных переменных от двух свободных.

Для нахождения первоначального базисного решения разобьем переменные на две группы – базисные и свободные. Так как определитель, составленный из коэффициентов при дополнительных переменных х₃,х₄ и х₅ отличен от нуля, то эти переменные можно взять в качестве базисных на первом шаге решения задачи. При выборе базисных переменных на первом шаге не обязательно составлять определитель из их коэффициентов и проверять, равен ли он нулю. Достаточно воспользоваться следующим правилом: в качестве базисных переменных на первом шаге следует выбрать (если возможно) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.

1 Шаг. Базисные переменные: х3, х4 и х5.

Свободные переменные: х₁, х₂.

Выразим базисные переменные через свободные:

(1)

Так как базисное решение лежит на границе ОДР, то положим свободные переменные равными нулю и получим следующее допустимое базисное решение: Х₁=(0; 0; 18; 16; 5; 21) (или первый опорный план). Поскольку это решение допустимое, то нельзя отбросить возможность того, что оно оптимальное. Выразим целевую функцию через свободные переменные: F=640х₁+464x₂=0, F(X₁)=0. Легко понять, что значение целевой функции F можно увеличить за счет увеличения любой из свободных переменных, входящих в выражение для F с положительным коэффициентом. Это можно осуществить, перейдя к новому допустимому базисному решению, в котором эта переменная будет базисной. В данном примере для увеличения F можно переводить в базисные либо х₁, либо х₂, так как обе эти переменные входят в выражение для F со знаком «плюс». Для определенности в такой ситуации лучше выбирать переменную, имеющую больший коэффициент, т.е. в данном случае – х₁.

Каждое уравнение системы ограничений накладывает свое ограничение на рост переменной х₁. Поскольку необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными, то должны выполняться следующие неравенства (при этом х₂=0 как свободная переменная) :

Очевидно, что сохранение неотрицательности всех переменных (допустимость решения) возможно, если не нарушается ни одна из полученных во всех уравнениях границ. В данном примере наибольшее возможное значение для переменной х₁ определяется как . При х₁=13,6 переменная х₃ обращается в нуль и переходит в свободные. Уравнение, где достигается наибольшее возможное значение переменной, переводимой в базисные (т.е. где оценка минимальна) называется разрешающим.

2 Шаг. Базисные переменные: х1, х4 и х5.

Свободные переменные: х₂, х₃.

Выразим новые базисные переменные через свободные, начиная с разрешающего уравнения. Его далее используем для преобразования оставшихся уравнений системы.

(2)

Положив свободные переменные равными 0, получим второе решение задачи: F=(13,6; 0; 0; 57,6; 52,8 )=8704.

Дальнейшее увеличение целевой функции возможно только за счет увеличения х₂, так как переменная х₃ входит в выражение для целевой функции с отрицательным коэффициентом, а это значит, что увеличить функцию F она может только принимая отрицательные значения. Повторяя рассуждения первого шага, мы получим из системы (2) наибольшее возможное значение для переменной х₂: . Второе уравнение становится разрешающим, переменная х₂ - базисной, а х₄ – свободной.

3 Шаг. Базисные переменные: х1, х2 и х5.

Свободные переменные: х₃, х₄.

Выразим новые базисные переменные через свободные, начиная с разрешающего уравнения. Его далее используем для преобразования оставшихся уравнений системы.

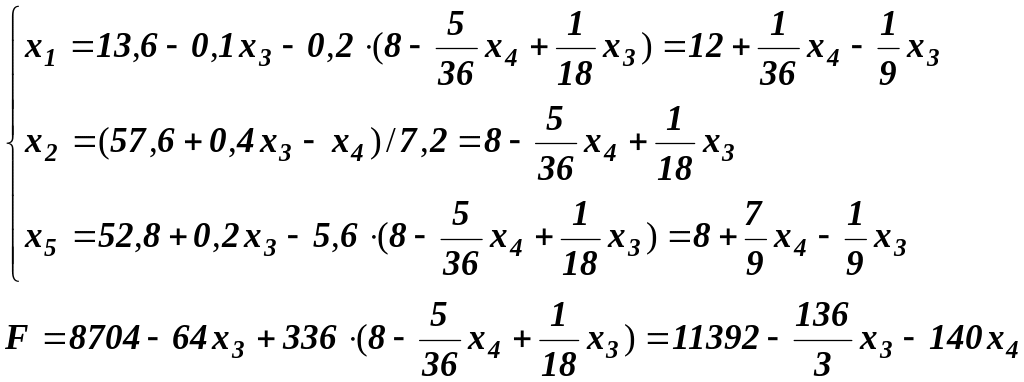
Положив свободные переменные равными 0, получим третье решение задачи: F=(12; 8; 0; 0; 8 )=11392. Это значение оптимально, так как его увеличения нельзя достигнуть, не нарушив ограничений задачи.

Теперь можно в общем виде сформулировать критерий оптимальности решения при отыскании максимума целевой функции: если в выражении целевой функции через свободные переменные отсутствуют положительные коэффициенты при свободных переменных, то решение оптимально.

При определении минимума целевой функции Z возможны два пути:

1. отыскать максимум функции F, полагая F= -Z и учитывая, что

Z_min= -F_max;

2. модифицировать симплексный метод: на каждом шаге уменьшать целевую функцию за счет той свободной переменной, которая входит в выражение целевой функции с отрицательным коэффициентом. Критерий оптимальности решения при отыскании минимума целевой функции будет выглядеть следующим образом: если в выражении целевой функции через свободные переменные отсутствуют отрицательные коэффициенты при свободных переменных, то решение оптимально.

Дополнение: Сформулируем все возможные случаи, возникающие при оценке наибольших возможных значений переменных для перевода в симплексном методе свободных переменных в базисные. Обозначим х_i – переводимая свободная переменная, b_j- свободный член, a_ij – коэффициент при х_i. В общем виде уравнение х_j=b_j+…+ a_ijx_i+… определяет наибольшее возможное значение х_i по следующим правилам:

1. х_i=|b_j/a_ij|, если b_j и a_ij разного знака и ,

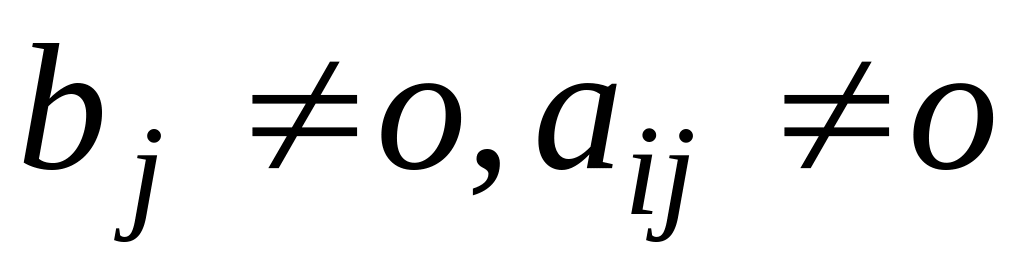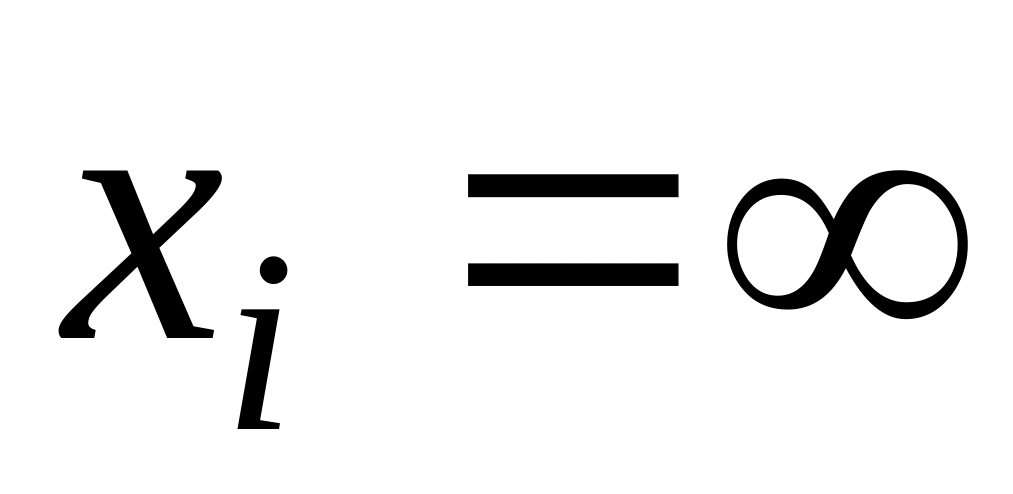2. , если b_j и a_ij одного знака и ,

3. х_i=0, если b_j = 0 и a_ij < 0,

4. , если b_j = 0 и a_ij > 0,

5. , если a_ij = 0.