Лекция 33-34

Лекция 33-34. Транспортные задачи. Экономико-математическая модель закрытой транспортной задачи. Нахождение первоначального базисного распределения поставок. Критерий оптимальности базисного распределения поставок. Модифицированный симплекс-метод, метод потенциалов. Экономико-математическая модель открытой транспортной задачи. Сведение решения открытой транспортной задачи к закрытой. Использование графов при решении транспортных задач.

Транспортные задачи – это класс условно-экстремальных задач, принадлежащих к разделу линейное программирование. Линейное программирование - это раздел математики, в котором изучаются методы решения задач на отыскание экстремума линейной функции нескольких переменных при наличии ограничений в виде линейных уравнений и неравенств.

Транспортной задачей линейного программирования называется задача определения оптимального плана перевозок некоторого груза из m пунктов отправления в n пунктов назначения .

Рассмотрим транспортную задачу, в которой критерием оптимальности является минимальная стоимость перевозок всего груза. Обозначим через стоимость перевозки единицы груза из i-го пункта отправления в j-ый пункт назначения, через - запасы груза в i-ом пункте назначения, - потребности в грузе j-го получателя, - количество груза, перевозимого из i-го пункта отправления j-му получателю. Тогда задачу можно записать следующим образом : найти минимум , при условиях: (1)

(2)

Условия (1) отражают полное удовлетворение потребностей j-го потребителя при перевозках и дают уравнения баланса по столбцам таблицы поставок. Условия (2) отражают полный вывоз запасов товара со склада i-го поставщика и дают уравнения баланса по строкам таблицы поставок. Условия (1) и (2) образуют систему ограничений.

Дадим математическую формулировку транспортной задачи в общей постановке: на множестве неотрицательных ( допустимых ) решений системы ограничений (1) и (2) найти такое решение , при котором значение линейной функции минимально.

Критерии для решения вопроса о минимальности функции F могут быть различными. Мы будем рассматривать транспортные задачи в следующей постановке: требуется найти объемы перевозок для каждой пары «поставщик-потребитель» так, чтобы:

1. мощности всех поставщиков были реализованы;

2. спросы всех потребителей были удовлетворены;

3. суммарные затраты на перевозку были бы минимальны. Другими словами, в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.

Если общее количество груза на складах равно суммарной потребности в нем всех потребителей, т.е. , то транспортная задача называется закрытой ( уравновешенной или сбалансированной ).

Если это условие не выполняется, то такая транспортная задача называется открытой (неуравновешенной или несбалансированной). Открытую задачу при решении легко свести к закрытой добавлением фиктивного потребителя, если запасы грузов превышают потребности в нем, при этом потребность фиктивного получателя . Если потребности в грузе превышают его запасы, то вводится фиктивный поставщик у которого имеется груз .

Можно показать, что закрытая транспортная задача всегда имеет решение.

Как и любая задача линейного программирования, транспортная задача может быть решена при помощи симплекс-метода. Однако, ввиду некоторых особенностей экономико-математической модели:

1. система ограничений есть система уравнений (т.е. транспортная задача задана в канонической форме);

2. каждая переменная входит в систему ограничений два раза: один раз – в систему (1) и один раз – в систему (2);

3. коэффициенты при переменных системы ограничений равны единице или нулю;

существуют другие, менее громоздкие методы. Прежде чем перейти к описанию одного из них, отметим без доказательства тот факт, что систему ограничений транспортной задачи можно разрешить относительно m+n-1 неизвестной. Эти неизвестные будут называться базисными, а остальные - свободными.

Рассмотрим решение закрытой транспортной задачи методом потенциалов. Этот метод является модификацией симплексного метода применительно к транспортной задаче.

Пример 1: Четырем предприятиям для производства продукции необходимо завезти 120, 50, 190 и 110 единиц сырья. Сырье сосредоточено в трех местах его получения, а запасы, соответственно равны 160, 140 и

170 единиц. Тарифы перевозок задаются матрицей 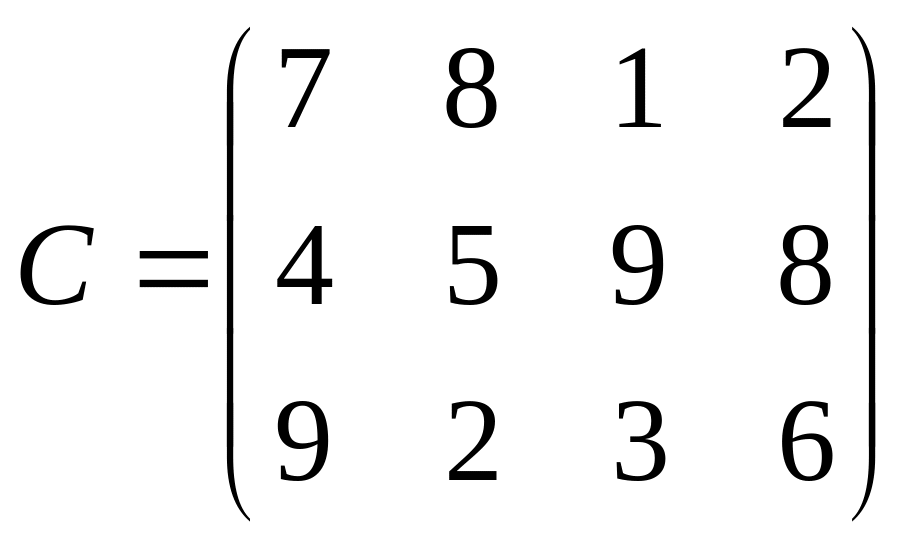. Составить план перевозок, при котором общая стоимость перевозок является минимальной. Проверяем сбалансированность задачи: величина потребностей 120 + 50 + 190 + 110 = 470. Запасы груза равны : 160 + 140 + 170 = 470. Значит, задача закрытая.

Поскольку метод потенциалов это, по существу, тот же симплексный метод, то при решении мы будем переходить от одного базисного распределения поставок к другому в сторону невозрастания целевой функции вплоть до оптимального решения. Для начала такого движения требуется исходное базисное распределение поставок – так называемый опорный план.

Для того, чтобы составить первый опорный план, условия задачи удобно записать в виде следующей таблицы:

ПН ПО		В1		В2		В3		В4		ui
		120		50		190		110
A1	160	7	7	8	8	160	1	-2	2	0
A2	140	120	4	1	5		9	20	8	4
A3	170	7	9	50	2	30	3	90	6	2
vj		0		0		1		4

Первые два столбца отведены под наименования пунктов отправления (ПО) и запасов сырья в них. Первые две строки отведены под наименования пунктов назначения (ПН) и количества сырья, потребляемого в них. В правом верхнем углу клеток таблицы указаны стоимости перевозок единицы груза от i-го поставщика j-му получателю. Последняя строка и последний столбец отведены для оценки найденного решения.

Первый опорный план можно составить разными способами. Наиболее распространенным из них можно считать метод минимальной стоимости перевозок. Сущность его состоит в следующем. Просматриваются все тарифы и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать m+n-1 занятых клеток. В процессе заполнения таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда полностью исчерпывается запас груза и полностью удовлетворяется спрос (вырожденная задача). В этом случае в необходимое количество свободных клеток надо записать число 0 – «нуль-загрузка», условно считая такую клетку занятой. Тем самым, мы получаем необходимое количество m+n-1 занятых клеток. Однако число 0 записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками. (подробнее эта проблема будет рассмотрена позднее)

Вернемся к примеру 1. В таблице найдем клетку с минимальным тарифом. В нашем случае это клетка на пересечении первой строки и третьего столбца. Заносим в нее значение . Исключаем из рассмотрения первую строку. Аналогичным образом выбираем значение (тариф 2), исключаем второй столбец. Далее удовлетворяем остаток потребностей заказчика за счет перевозки со склада 30 единиц груза (тариф 3), исключаем третий столбец. По тому же алгоритму заполняем (тариф 4), можно сразу остаток груза отправляем , т.к. другого варианта распределить оставшийся на этом складе груз нет. Исключили вторую строку. Осталось распределить груз из , 120 единиц достанется ( ), а 20 единиц груза достанется ( ). Мы получили первый план с m+n-1=3+4-1=6 занятых клеток. Задача невырожденная.

После заполнения таблицы нужно проверить выполнение требований (4) и (5). Оценим найденный план. Подсчитываем стоимость перевозок:

F = 160*1 + 120*4 + 20*8 + 50*2 + 30*3 + 90*6 =1530.

Теперь необходимо оценить полученный план на предмет его оптимальности. Для этого введем систему m+n чисел , где – потенциал строки, а – потенциал столбца. Конкретные значения потенциалов для каждого плана находятся из условия ( для занятых клеток ).

Получим для нашей задачи. Пусть числа - потенциалы строк, - потенциалы столбцов, которые удовлетворяют условиям: ( для занятых клеток ).

Для начала выбираем произвольно значения или , например, =1 и заносим его в первую строку, т.к. в этой строке занят третий столбец, то , откуда . В этом столбце занята еще третья строка, значит => . Затем аналогично получаем => .

=>

=>

=>

После этого вычисляем оценки пустых клеток по формулам: .

Эти оценки заносим в клетки в левый верхний угол. Критерий оптимальности плана распределения поставок формулируется следующим образом: план распределения поставок оптимален тогда и только тогда, когда оценки всех свободных клеток неотрицательны. Если имеются отрицательные оценки, то возможно улучшение плана. Для этого составляем цикл улучшения плана. Циклом в матрице будем называть ломаную с вершинами в клетках и звеньями, лежащими вдоль строк и столбцов матрицы, удовлетворяющую условиям:

1. ломаная должна быть связной, т.е. из любой её вершины можно попасть в любую другую вершину по звеньям ломаной;

2. в каждой вершине ломаной встречаются два звена, одно из которых располагается по строке, другое – по столбцу.

Циклом пересчета является цикл в матрице (многоугольник), одна вершина которого находится в клетке с отрицательной оценкой (если их несколько, то в клетке с наименьшей оценкой), остальные в занятых клетках. Для каждой свободной клетки базисного распределения поставок существует и притом единственный цикл пересчета. Обычно его отмечают на плане штриховыми линиями. Так как в клетку с отрицательной оценкой при пересчете будет занесено число, то отмечаем ее знаком "+", в соседней вершине вычтем такое же число, ставим знак "-", в следующую - занесем и т.д. Для перемещения по контуру выбираем наименьшее из всех чисел, попавших в клетки, отмеченные знаком "-". Другими словами, поставка, передаваемая по циклу, определяется как минимум среди поставок в клетках цикла со знаком "-". В нашем случае - это число . После этого клетка (3,4) считается свободной, а клетка (1,4) – заполненной. Баланс цикла ( сумма по каждой строке и по каждому столбцу, входящему в цикл ) при этом не нарушается. Цикл составлен удачно, если разница между суммой тарифов в клетках с "+" и суммой тарифов в клетках с "-" равна отрицательной оценке клетки, для которой этот цикл составляется. Приведем схемы наиболее часто встречающихся циклов пересчета.

а ) б) в) г)

е )

Построенный цикл пересчета:

(-) (1,3) (1,4) (+)

160	1		2	2
30	3		90	6

(+) (3,3) (3,4) (-)

Выполненный цикл пересчета:

(-) (1,3) (1,4) (+)

70	1		2 90	2
120	3			6

(+) (3,3) (3,4) (-)

Выпишем новое опорное решение и оценим его по процедуре, описанной ранее.

ПН ПО		В1		В2		В3		В4		ui
		120		50		190		110
A1	160	9	7	8	8	70	1	90	2	0
A2	140	120	4	-1	5	2	9	20	8	6
A3	170	9	9	50	2	120	3	2	6	2
Vj		-2		0		1		2

Подсчитываем стоимость перевозок при новом плане : F = 4*120 + 50*2 + 70*1 + 120*3 + 90*2 + 20*8 = 1350. Стоимость уменьшилась, однако есть пустая клетка (2,2) с отрицательной оценкой (-1). Строим для нее цикл пересчета.

		(-) (+)	70	1	(+) (-)	90	2
- 1	5		2	9		20	8
50	2		120	3

(+)

(-)

Выполним построенный цикл пересчета. По циклу переносим min(70,20,50)=20.

		(-) (+)	50	1	(+) (-)	110	2
- 1 20	5		2	9			8
30	2		140	3

(+)

(-)

Составим новый план. Вновь произведем его оценку на оптимальность по приведенному выше алгоритму. В данном (третьем по счету плане) оценки всех пустых клеток неотрицательны, значит, этот план оптимален. Стоимость перевозок при этом: F = 50 + 220 + 420 + 60 + 100 + 480 = 1330. План перевозок таков: , , , , , .

Рассмотренная нами транспортная задача характеризуется тем, что сумма запасов грузов на станциях отправления равна суммарной потребности в пунктах назначения. На практике же часто встречаются задачи, в которых это равенство нарушено, т.е. .

Как уже было сказано выше, открытую транспортную задачу можно легко свести к уже рассмотренной закрытой транспортной задаче, если ввести или фиктивную пункт отправления с таким количеством запаса, или фиктивный пункт назначения с такой потребностью, чтобы сумма запасов на пунктах отправления была равна сумме всех потребностей в пунктах назначения. При этом надо запретить вывозить груз с фиктивных пунктов отправления и ввозить груз в фиктивные пункты назначения. Этот запрет можно выразить, например, следующим образом: назначить равными нулю стоимости перевозок груза с фиктивных пунктов отправления или в фиктивные пункты назначения. Это и будет означать, что груз на самом деле не вывозится и не ввозится в фиктивные пункты, так как за его транспортировку ничего не платится. После такого преобразования задачу можно решать уже рассмотренным способом.

В качестве примера рассмотрим решение следующей задачи.

Пример 2: Найти оптимальное распределение поставок для транспортной задачи. Условие задачи представлено в следующей таблице:

ПН ПО		В1		В2		В3		В4
		45		35		55		65
A1	40		4		1		2		5
A2	60		3		2		3		7
A3	90		4		4		5		2

В данном случае суммарный спрос потребителей больше, чем суммарная мощность поставщиков (45 + 35 + 55 + 65 = 200 > 40 + 60 + 90 = 190 ). Введем фиктивного поставщика и в таблицу поставок добавим дополнительную строку так, чтобы задача стала закрытой. Для этого мощность фиктивного поставщика следует принять равной 10 = 200 - 190. Коэффициенты затрат этой добавленной строки определяются равными нулю. Таким образом, мы свели открытую транспортную задачу к закрытой. Первоначальное распределение поставок для сформулированной закрытой транспортной задачи найдем, например, по методу наименьшей стоимости. В результате приходим к следующему первому базисному распределению поставок:

ПН ПО		В1		В2		В3		В4		ui
		45		35		55		65
A1	40	2	4	35	1	5	2	5	5	0
A2	60	10	3		2	50	3	6	7	1
A3	90	35	4	1	4	1	5	55	2	2
A4	10	-2	0	-1	0	-2	0	10	0	0
vj		2		1		2		0

Установим, оптимально ли это распределение – получим оценки методом потенциалов. Так как среди оценок свободных клеток есть отрицательные, то найденное распределение не оптимально. Построим цикл пересчета для одной из клеток с наименьшей отрицательной оценкой (-2). Поставка, передаваемая по циклу, равна min(50,35,10)=10.

10	3	(-) (+)	50	3	(+) (-)	2
35	4			5		55	2
			- 2	0		10	0

(+)

(-)

Передвигая по циклу поставку, равную 10 единицам, приходим к следующему распределению поставок. Найдем оценки свободных клеток распределения. Так как оценки всех свободных клеток неотрицательны, то распределение поставок оптимально.

ПН ПО		В1		В2		В3		В4		ui
		45		35		55		65
A1	40	2	4	35	1	5	2	5	5	0
A2	60	20	3		2	40	3	6	7	1
A3	90	25	4	1	4	1	5	65	2	2
A4	10	0	0	1	0	0 10	0	2	0	-2
vj		2		1		2		0

F = 3*20+4*25+1*35+3*40+0*10+2*65 = 445.

В случае, когда суммарная мощность поставщиков больше суммарной мощности потребителей, в рассмотрение вводится фиктивный потребитель, а к таблице поставок присоединяется дополнительный столбец. Коэффициенты затрат этого добавочного столбца принимают равными нулю.

Существует более эффективный способ построения циклов пересчета – метод графов. Полностью его можно изучить в книге В.А. Волков «Элементы линейного программирования». Мы рассмотрим только две практические задачи, использующие метод графов.

Первая из них – решение проблемы выбора свободных клеток для «нуль-загрузки» в вырожденных задачах.

Пример 3: имеется транспортная задача с заданным распределением поставок.

ПН ПО		В1		В2		В3		В4		ui
		45		85		35		55
A1	95	45	5	50	4		13		9
A2	35		2		7	35	9		8
A3	55		9	35	7		11	20	7
A4	35		1		6		1	35	1
vj

Задача является вырожденной, т.к. число занятых клеток равно шести, вместо требуемых семи. Для использования метода потенциалов нужно одну из свободных клеток сделать занятой с «нуль-загрузкой». Выбор свободной клетки проведем при помощи построения графа по занятым клеткам

Под графом будем понимать множество точек плоскости или пространства и множество дуг, соединяющих все или некоторые из этих точек. Точки называют вершинами графа. Дуга графа соединяет две вершины. Та вершина, на которую указывает стрелочка, является конечной. А вершина, из которой исходит дуга графа – начальной. Начальные вершины могут соответствовать только пунктам отправления, а конечные – пунктам назначения.

Построим граф при заданном распределении поставок.

Рис.1.

Непрерывными дугами указаны ненулевые поставки заданного распределения. Граф поставок получается несвязным. Он состоит из двух частей, значит, чтобы получить первый опорный план необходимо связать эти две части графа любой возможной дугой из Аi в Bj. Этой дуге в таблице будет соответствовать клетка с координатами (i,j) с «нуль-загрузкой». Таким образом, мы получим необходимое количество занятых клеток для дальнейшего решения транспортной задачи. Возможно множество различных вариантов связывания графа. Приведем два примера:

Рис.2. Рис.3.

Пусть мы выбрали вариант с рисунком 2, тогда получим следующее распределение поставок.

ПН ПО		В1		В2		В3		В4		ui
		45		85		35		55
A1	95	45	5	50	4	0	13		9
A2	35		2		7	35	9		8
A3	55		9	35	7		11	20	7
A4	35		1		6		1	35	1
vj

Далее задача решается стандартным образом согласно приведенному выше алгоритму решения уравновешенной (закрытой) задачи.

Вторая прикладная задача – построение неочевидного цикла пересчета в больших транспортных задачах. В этом случае метод графов дает оптимальный способ решения этой проблемы.

Пример 4: имеется транспортная задача на определенном этапе решения. Распределение поставок на этом этапе представлено в таблице. Необходимо построить цикл пересчета для клетки с наибольшей (по модулю) отрицательной оценкой (-7).

ПН ПО		В1		В2		В3		В4		ui
		20		30		10		40
A1	30	- 20	5	+ 10	1	2	3	6 -2	6	0
A2	20	-6	2	- 20	4	+ 0	4	-2	3	3
A3	50	-7 +	3	-1	5	- 10	6	40	7	5
vj		5		1		1		2

Для того, чтобы построить цикл пересчета построим граф по занятым клеткам:

Рис.4.

Требуемый цикл пересчета – это замкнутая ломаная, включающая встраиваемую дугу . Чтобы его получить, нужно убрать лишние дуги вместе с конечными вершинами.

Рис.5.

Весь оставшийся, урезанный граф перенесем обратно в таблицу и получим цикл пересчета. Цикл пересчета можно выписать отдельно, а можно нанести прямо в таблице (см. таблицу).

Задачи для самостоятельного решения.

1. Решить следующие уравновешенные ( закрытые ) транспортные задачи:

а).

ПН ПО		В1		В2		В3		В4		В5
		60		140		130		80		90
A1	100		11		4		8		3		10
A2	250		5		9		20		7		4
A3	150		7		15		6		12		18

Ответ: 2800.

б).

ПН ПО		В1		В2		В3		В4		В5
		100		120		60		80		140
A1	150		4		8		5		7		16
A2	150		9		3		4		10		8
A3	200		13		6		11		15		12

Ответ: 3450.

в).

ПН ПО		В1		В2		В3		В4		В5
		160		140		200		80		120
A1	300		15		7		20		8		14
A2	200		4		15		16		9		7
A3	200		10		6		12		11		5

Ответ: 5980.