Лекция 8

Лекция 8. Линейное преобразование вектора, запись в матричном виде. Собственные числа и собственные векторы матрицы, характеристическое уравнение. Решение характеристического уравнения. Нахождение собственных векторов в случае различных и кратных корней. Метод итераций для определения наибольшего собственного числа.

Линейные пространства.

Дадим определение линейного пространства.

Пусть дано множество ; его элементы будут обозначаться малыми латинскими буквами: Пусть во множестве определены операция сложения, ставящая в соответствие всякой паре элементов из однозначно определенный элемент из , называемый их суммой, и операция умножения на действительное число, причем произведение элемента на число однозначно определено и принадлежит к . Элементы множества будут называться векторами, а само – действительным линейным пространством, если указанные операции обладают следующими свойствами:

1. Сложение коммутативно, .

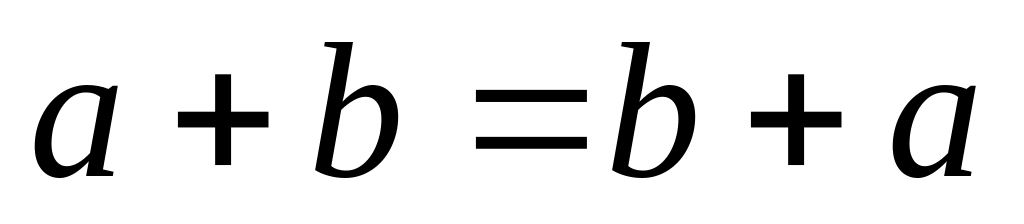2. Сложение ассоциативно,

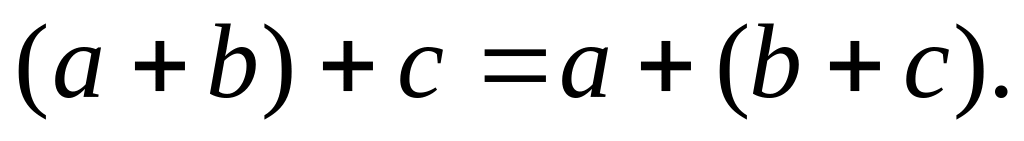
3. В V существует нулевой элемент 0, удовлетворяющий условию: 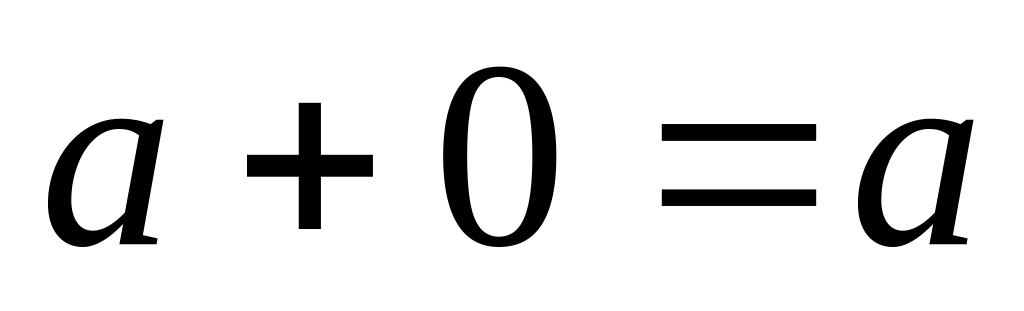для всех из .

4. Для всякого элемента в существует противоположный элемент - , удовлетворяющий условию: .

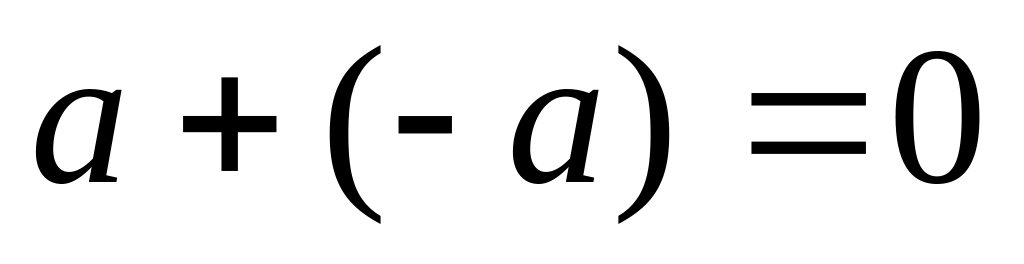Дальнейшие аксиомы связывают умножение на число со сложением и с операциями над числами. Именно, для любых элементов из , для любых действительных чисел и для действительного числа 1 должны иметь место равенства.

5. 

6. 

7. 

8. 

Линейные преобразования линейного пространства.

Если задано правило, по которому каждому элементу (вектору) линейного пространства поставлен в соответствие элемент (вектор) того же пространства, то говорят, что задано преобразование этого пространства. Элемент называется образом элемента при рассматриваемом преобразовании. Если преобразование обозначено через , то образ вектора будем обозначать . Преобразования также называются операторами.

Преобразование называется линейным, если сумму любых двух векторов оно переводит в сумму образов этих векторов

,

а произведение любого вектора на любое число переводит в произведение образа вектора на это же число .

Из этого определения немедленно вытекает, что линейное преобразование линейного пространства переводит любую линейную комбинацию данных векторов в линейную комбинацию ( с теми же коэффициентами ) образов этих векторов.

(1)

Базис пространства.

Линейно независимая система векторов, через которые линейно выражается каждый вектор пространства, называется базисом пространства. Пусть базис этого пространства, так как всякий вектор пространства одно однозначно представляется в виде линейной комбинации векторов , то ввиду (1) образ вектора с теми же коэффициентами выражается через образы векторов , т.е. всякое линейное преобразование пространства однозначно определяется заданием образов . Из координат образов мы можем составить матрицу А. Строками этой матрицы будут координаты образов базисных векторов. Покажем, что образ любого вектора х мы можем получить умножив матрицу А на х. Возьмем произвольный вектор х, . В силу (1) , что равносильно матричному равенству . Другими словами, строка координат вектора равна строке координат вектора х, умноженной справа на матрицу А линейного преобразования , все в базисе е: .

Линейное преобразование полностью характеризуется его матрицей. Поэтому действия над такими преобразованиями сводятся к действиям над их матрицами.