Решение систем линейных алгебраических уравнений. Метод Крамера. В общем виде система m линейных уравнений с n неизвестными записывается так: (11)

Уравнения системы считаются пронумерованными: первое, второе и т.д. Числа - называются неизвестными системы; - коэффициентами при неизвестных системы.

Коэффициент при неизвестном в i-ом уравнении обозначается через ,где первый индекс i указывает номер уравнения, в котором находится данный коэффициент, а второй индекс j – номер неизвестного, при котором находится данный коэффициент. Например, коэффициент находится во втором уравнении системы при неизвестном .

Числа - называются свободными членами системы.

Решением системы линейных уравнений называется любая совокупность чисел , которая будучи подставленной на место неизвестных в уравнения данной системы, обращает все эти уравнения в тождества.

Система уравнений называется совместной, если она имеет решение. Если система уравнений не имеет решения, то она называется несовместной ( или противоречивой ). Примером несовместной системы служит система:

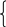
Совместная система линейных уравнений может иметь одно или несколько решений и называется определенной, если имеет одно единственное решение, и неопределенной, если имеет больше одного решения. Так, система определена, она имеет решение (1,3). Это решение единственно. С другой стороны, система неопределенна, так как имеет бесконечно много решений вида где число k – произвольно, причем этими решениями исчерпываются все решения системы.

Две системы линейных уравнений с одним и тем же числом неизвестных называются эквивалентными, если они или обе несовместны, или обе совместны и имеют одни и те же решения.

Элементарными преобразованиями системы линейных уравнений называются три типа преобразований:

1. перестановка двух уравнений системы;

2. умножение обеих частей уравнения системы на любое отличное от нуля число;

3. прибавление ( вычитание ) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Можно доказать, что элементарные преобразования переводят данную систему линейных уравнений в эквивалентную. Выполнение элементарных преобразований равносильно выражению одного неизвестного через другие.

Система, в которой свободные члены равны нулю, называется однородной.

Правило Крамера. Пусть дана система двух линейных уравнений с двумя неизвестными

(12)

коэффициенты которой составляют квадратную матрицу второго порядка . Применяя к системе (12) метод уравнивания коэффициентов, мы получим:

Предположим, что . Тогда

Если посмотреть внимательно на получившиеся формулы, то легко видно, что их можно переписать в следующем виде:

.

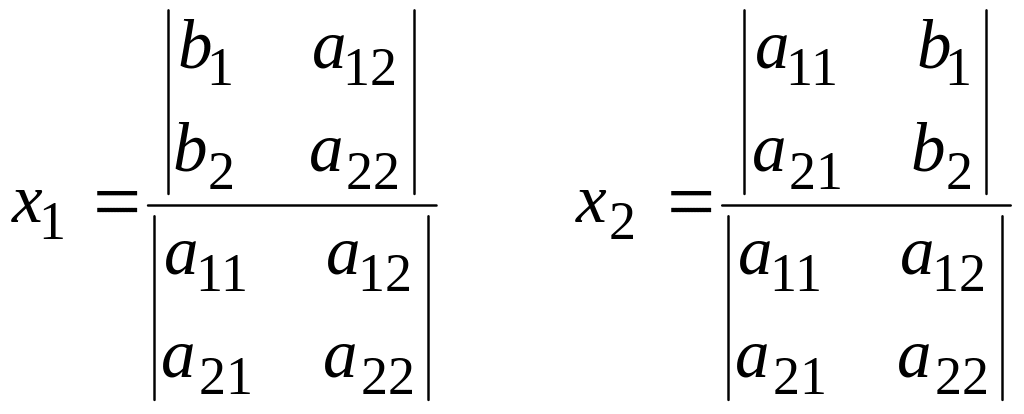Эти формулы называются формулами Крамера. Правило решения называется правилом Крамера и формулируется следующим образом:

Если определитель из коэффициентов системы уравнений отличен от нуля, то мы получим решение системы, беря в качестве значений для неизвестных дроби, общим знаменателем которых служит определитель из коэффициентов системы уравнений, а числителем для неизвестного является определитель, получающийся заменой в определителе i-го столбца (т.е. столбца коэффициентов при искомом неизвестном ) столбцом из свободных членов системы.

Приведем общую теорему.

Теорема Крамера. Система n линейных уравнений с n неизвестными, определитель которой отличен от нуля, всегда совместна и имеет единственное решение, вычисляемое по формулам