Решение систем линейных уравнений матричным методом.
Вернемся к системе (1) – к произвольной системе m линейных уравнений с n неизвестными. Таблица коэффициентов при неизвестных
(5)
называется матрицей коэффициентов при неизвестных. А столбцы
;
,
(6)
составленные из свободных членов и неизвестных системы (1), называются соответственно матрицей-столбцом (вектором-столбцом) свободных членов системы и матрицей-столбцом) (вектором-столбцом) неизвестных системы.
Если определить произведение АХ матрицы А на столбец Х как столбец, состоящий из сумм произведений элементов каждой из m строк матрицы А на элементы столбца Х, то систему (1) можно записать в виде одного матричного уравнения
(7)
Из этого матричного уравнения при заданных матрице А и матрице-столбце В должна быть определена матрица-столбец Х, содержащая неизвестные.
Если матрица А
квадратная (
)
и ее определитель
не равен нулю, то как мы выяснили в
предыдущей лекции, можно построить
такую матрицу
,
называемую обратной к матрице А,
что умножив слева обе его части уравнения
(7) на
( в предположении, что обратная матрица
существует ):
.
По определению обратной матрицы
,
следовательно
,
откуда
- (8) решение матричного уравнения
(7), а значит, и решение системы (1).
Если же матрица А системы (1) не квадратная, или она квадратная, но с нулевым определителем , то обратная к ней матрица не существует, и решение матричного уравнения (7) в матричной форме найдено быть не может (даже если само решение и существует). Это обстоятельство сильно снижает ценность матричного метода решения систем линейных уравнений. Он, как и метод определителей, не является универсальным методом их решения (в отличие от метода Гаусса). Но зато, когда эти методы могут быть применены (для квадратных систем, имеющих единственное решение), то они позволяют получить это решение по готовым формулам. А именно, по формулам Крамера в методе определителей, или по формуле (8) в матричном методе.
Пример 4. Решить матричное уравнение
Решение.
.Находим
.
Пример 5. Решить матричное уравнение
.
Решение.
Находим матрицу, обратную к А :
.
Системы линейных алгебраических уравнений с квадратной матрицей А может быть записана не только в виде AX=B, а еще и в виде XA=B, (9)
AXB=C,
(10) где
- квадратная матрица порядка n,
а B,C
и X
– матрицы, размеры которых соответствуют
правилам умножения матриц.
Рассмотрим
уравнение (9). Для решения уравнения (9)
умножим справа обе его части на
( в предположении, что обратная матрица
существует ):
.
По определению обратной матрицы
,
следовательно
,
откуда
.
Пример 6. Решить матричное уравнение
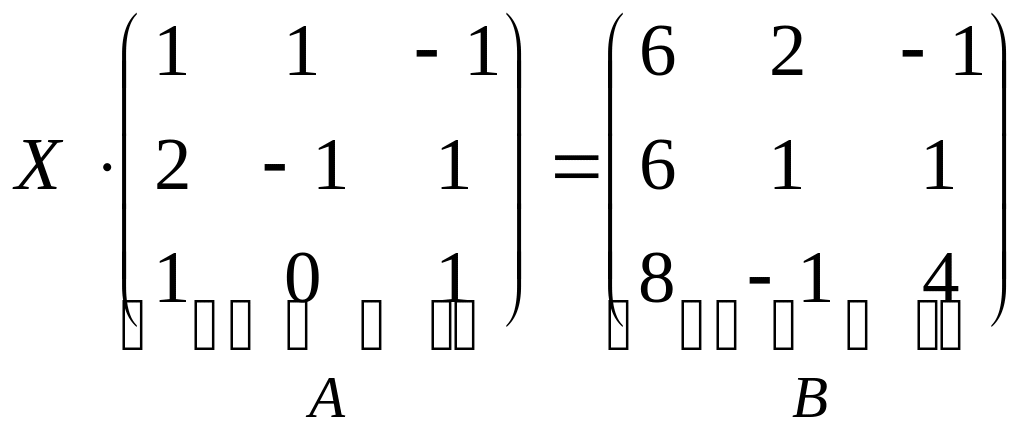
Решение.
.
.
.
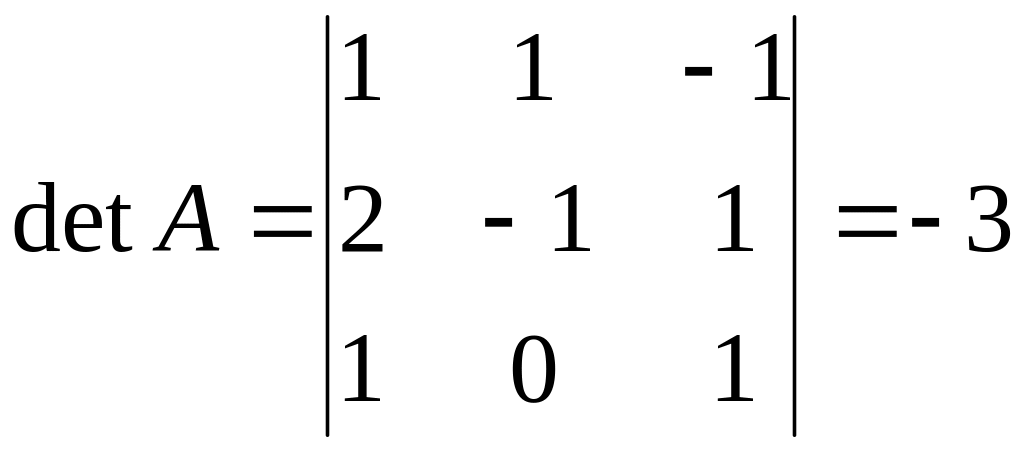Для решения
уравнения (10) умножим справа обе его
части слева на
( в предположении, что обратная матрица
существует ), а справа на
(
в предположении, что обратная матрица
существует ), тогда получим:
По
определению обратной матрицы
,
следовательно
,
откуда
Пример 7. Решить матричное уравнение
Решение.
Находим
