
Задача 8.34
В задачах 8.1-8.40 (конкретные параметры приведены в табл. 8.1) двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 8.1 области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
![]()
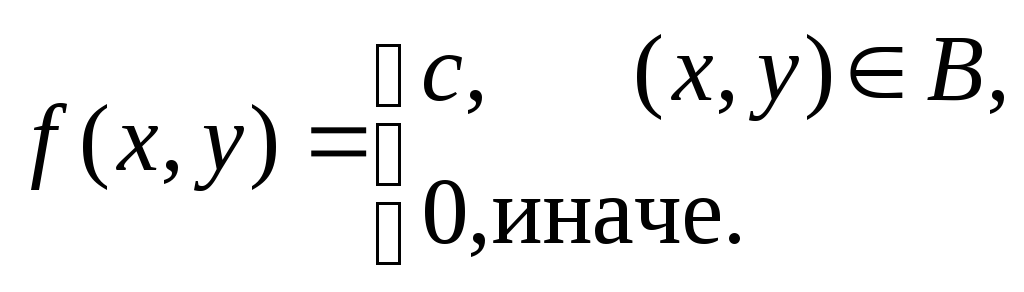
Вычислить коэффициент корреляции между величинами X и Y.

Рис. 8.1
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y1 |
y2 |
|
0 |
2 |
4 |
5 |
5 |
6 |
1 |
2 |
Решение:
-
Построим область B согласно координатам из таблицы и рисунка 8.1.
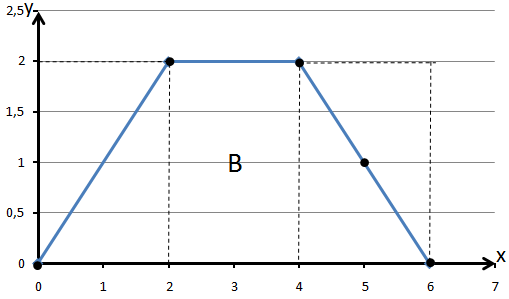
Проанализируем рисунок : область B ограничена сверху прямой y=2 , снизу y=0 ; слева прямой y=x , справа прямой y=6-x .
Следовательно, совместная плотность вероятности примет вид:
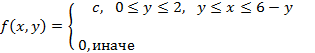
-
Найдём константу
 из условия нормировки:
из условия нормировки:
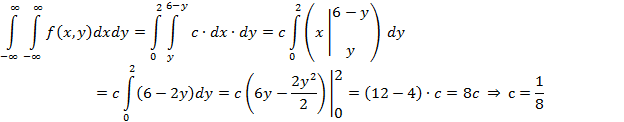
Таким образом:
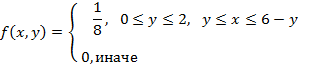
-
Вычислим математические ожидания:
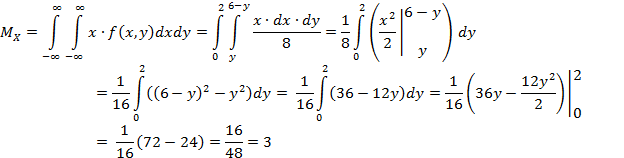
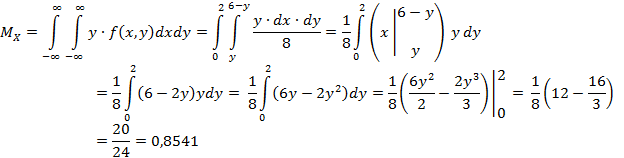
-
Вычислим дисперсии:
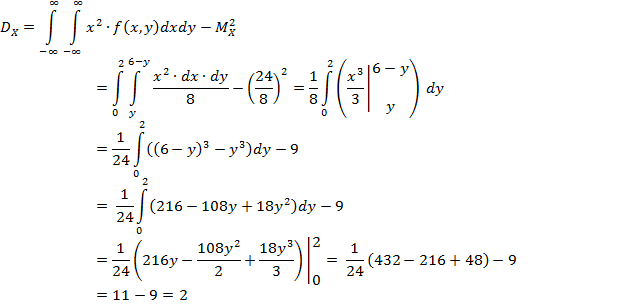
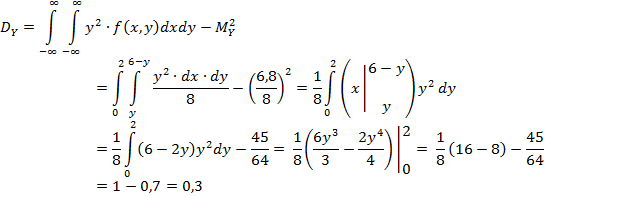
5)Вычислим корреляционный момент:
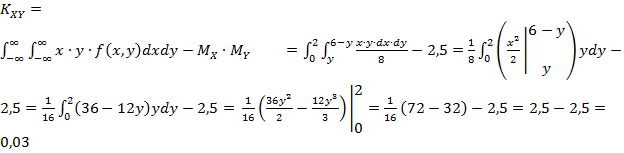 2
2
6)Вычислим коэффициент корреляции между величинами X и Y:
![]()
Ответ:![]()
Задача 9.38
В задачах 9.1-9.40 вычислить
математическое ожидание и дисперсию
величин U
и V, а так
же определить их коэффициент корреляции
![]() :
:
![]()
![]() .
.
Конкретные значения
коэффициентов
![]() и числовые характеристики случайных
величин
и числовые характеристики случайных
величин
![]() приведены в табл. 9.1.
приведены в табл. 9.1.
|
Вариант |
a0 |
a1 |
a2 |
b0 |
b1 |
b2 |
m1 |
m2 |
m3 |
D1 |
D2 |
D3 |
K12 |
K23 |
K13 |
|
9.38 |
9 |
7 |
8 |
-5 |
5 |
1 |
0 |
6 |
0 |
16 |
16 |
9 |
8 |
6 |
6 |
Решение:
![]()
![]()
![]()
![]()
Корреляционный момент равен:
![]()
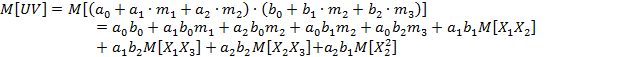
![]()
![]()
![]()
![]() =52
=52
![]()
![]()
![]()
Ответ:![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
Контрольная работа №2. Математическая статистика
Задача 10.79
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить точечные оценки математического ожидания и дисперсии;
- вычислить интервальные оценки математического ожидания и дисперсии (γ = 0,95);
- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия 2 и критерия Колмогорова ( = 0,05). График гипотетической функции распределения F0(x) построить совместно с графиком F*(x) в той же системе координат и на том же листе.
Одномерная выборка № 79:
-2.40 -5.01 -4.45 -4.82 -4.43 -2.38 -5.75 -1.63 -4.29 -1.52 -4.47 -1.67 -4.62 -1.39 -4.65 -5.11 -3.37 -0.83 -2.38 -2.81 -3.03 -1.37 -2.78 -4.14 -3.73 -2.74 -1.03 -2.53 -6.11 -1.87 -2.88 -4.23 -3.10 -4.53 -1.63 -1.93 -0.71 -1.16 -1.18 -4.72 -4.64 -3.43 -4.82 -3.28 -4.39 -5.66 -5.94 -1.36 -1.56 -4.40 -4.44 -1.08 -4.10 -5.05 -3.51 -2.56 -2.28 -5.00 -1.96 -3.89 -3.01 -3.52 -1.55 -3.13 -5.94 -2.42 -2.36 -2.13 -0.75 -5.44 -2.80 -5.48 -1.46 -5.82 -2.55 -6.08 -2.84 -0.83 -5.39 -3.89 -1.47 -3.25 -6.20 -1.77 -3.12 -1.05 -1.22 -5.01 -4.15 -1.47 -3.03 -5.15 -0.93 -1.02 -0.90 -5.78 -1.02 -3.38 -2.69 -5.99
Решение:
-
Получим вариационный ряд из исходного:

-
Построим график эмпирической функции непосредственно по вариационному ряду, так как F*(x) – неубывающая и практически все ступеньки графика имеют одинаковую величину
 (Рисунок 10,1).
(Рисунок 10,1).
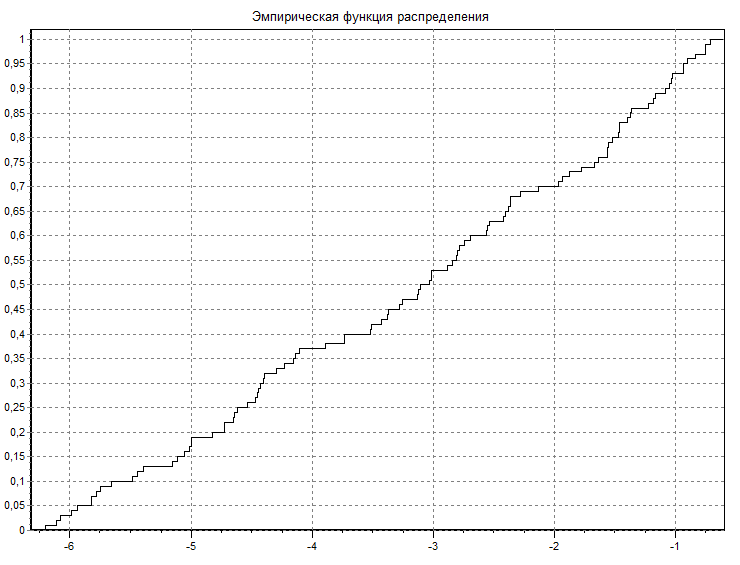
Рисунок 10.1
-
Построим гистограмму равноинтервальным способом (рисунок 10,2).
Для построения гистограммы составим интервальный статистический ряд, учитывая что длина у всех интервалов должна быть одинаковая.
![]() - количество интервалов;
- количество интервалов;
![]() - ширина интервала;
- ширина интервала;
![]() -
частота попадания СВ X
в j-ый
интервал;
-
частота попадания СВ X
в j-ый
интервал;
![]() - статистическая плотность
в j-ом
интервале.
- статистическая плотность
в j-ом
интервале.
Таблица 1 – Интервальный статистический ряд
-
j
Aj
Bj
hj
vj
pj*
fj*
1
-6,2
-5,65
0,549
10
0,1
0,182
2
-5,65
-5,1
0,549
5
0,05
0,091
3
-5,1
-4,55
0,549
10
0,1
0,182
4
-4,55
-4
0,549
12
0,12
0,218
5
-4
-3,45
0,549
5
0,05
0,091
6
-3,45
-2,91
0,549
11
0,11
0,200
7
-2,91
-2,36
0,549
15
0,15
0,273
8
-2,36
-1,81
0,549
5
0,05
0,091
9
-1,81
-1,26
0,549
13
0,13
0,236
10
-1,26
-0,71
0,549
14
0,14
0,255
X
f*(x)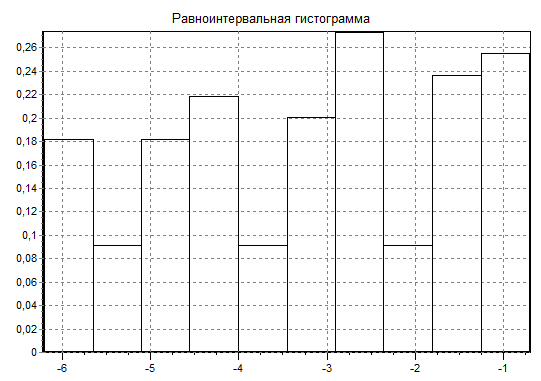
Рисунок 10.2
-
Построим гистограмму равновероятностным способом (рисунок 10,3).
Для построения гистограммы составим интервальный статистический ряд, учитывая что частота попадания СВ X в в каждый j-ый интервал должна быть одинаковая (Таблица 2).
Таблица 2 – Интервальный статистический ряд
-
j
Aj
Bj
hj
vj
pj*
fj*
1
-6,2
-5,57
0,63
10
0,1
0,158
2
-5,57
-4,82
0,75
10
0,1
0,133
3
-4,82
-4,42
0,405
10
0,1
0,247
4
-4,42
-3,63
0,79
10
0,1
0,126
5
-3,63
-3,06
0,56
10
0,1
0,178
6
-3,06
-2,63
0,44
10
0,1
0,227
7
-2,63
-2,04
0,58
10
0,1
0,172
8
-2,04
-1,5
0,55
10
0,1
0,182
9
-1,5
-1,06
0,43
10
0,1
0,232
10
-1,06
-0,71
0,35
10
0,1
0,281
f*(x)
X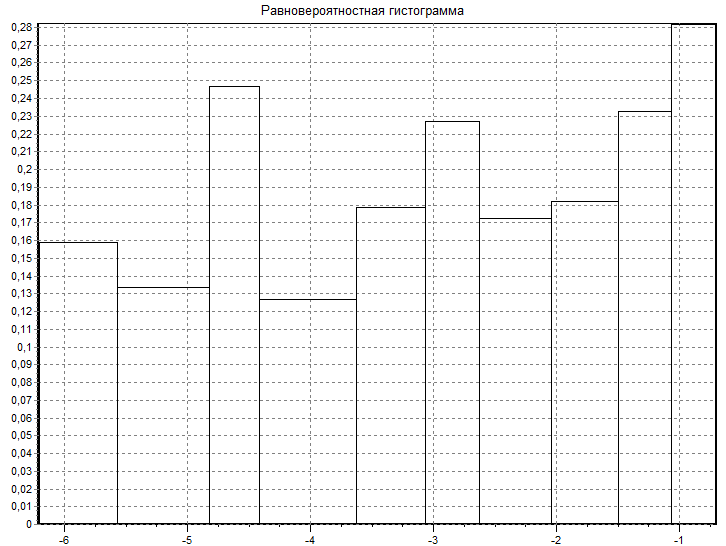
Рисунок 10,3
-
Вычислим точечные оценки математического ожидания и дисперсии:
![]()
![]()
-
Вычислим интервальные оценки математического ожидания и дисперсии (γ = 0,95):
![]()
![]()
![]()
![]()
![]()
-
По виду графика эмпирической функции распределения
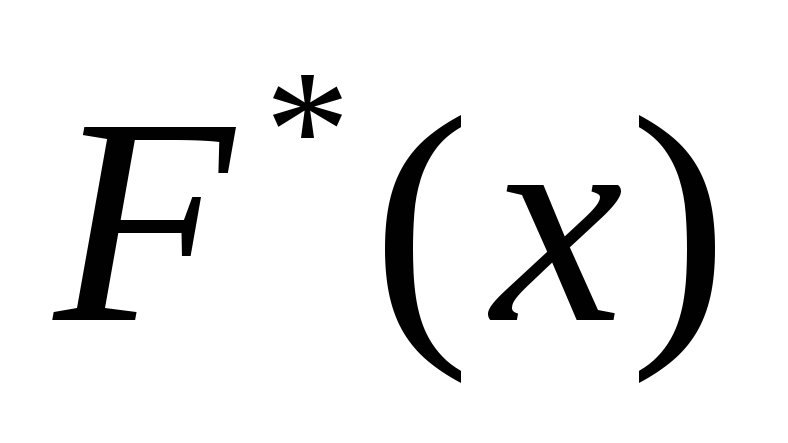 и
гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения
случайной величины X:
и
гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения
случайной величины X:
H0 – величина X распределена по экспоненциальному закону:
![]()
H1 – величина X не распределена по экспоненциальному закону
![]()
Таким образом получаем полностью определенную гипотетическую функцию распределения:
![]()
Проверим гипотезу об
экспоненциальном законе по критерию
Пирсона
![]() .
Вычислим значение критерия
.
Вычислим значение критерия
![]() на основе равноинтервального
статистического ряда:
на основе равноинтервального
статистического ряда:

Теоретические вероятности попадания в интервалы вычислим по формуле:
![]()
Таблица 6 – Результаты расчётов
-





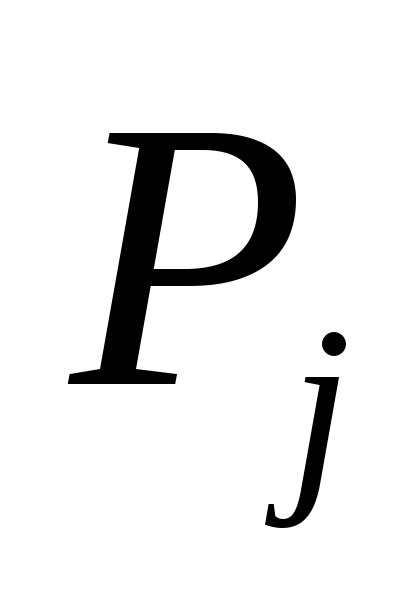


1
-6,2
-5,65
0
0,09
0,09
0,1
0,001111
2
-5,65
-5,1
0,09
0,14
0,05
0,05
3,85E-33
3
-5,1
-4,55
0,14
0,25
0,11
0,1
0,000909
4
-4,55
-4
0,25
0,365
0,115
0,12
0,000217
5
-4
-3,45
0,365
0,415
0,05
0,05
3,85E-33
6
-3,45
-2,91
0,415
0,535
0,12
0,11
0,000833
7
-2,91
-2,36
0,535
0,67
0,135
0,15
0,001667
8
-2,36
-1,81
0,67
0,725
0,055
0,05
0,000455
9
-1,81
-1,26
0,725
0,86
0,135
0,13
0,000185
10
-1,26
-0,71
0,86
0,99
0,13
0,14
0,000769
Сумма:
1
1
0,006147
Проверим правильность вычислений
![]() :
:
![]()
Вычислим критерий Пирсона:

Определим число степеней свободы:
![]()
Выбираем критическое значения
критерия Пирсона из таблицы для степени
свободы
![]() и
заданного уровня значимости
и
заданного уровня значимости
![]() :
:
![]()
Так как условие выполняется, то гипотеза H0 об экспоненциальном законе распределения принимается (нет оснований ее отклонить).
8) Проверим гипотезу при помощи критерия
Колмогорова. Для этого построим
график гипотетической функции
распределения
![]() в
одной системе координат с эмпирической
функцией
в
одной системе координат с эмпирической
функцией
![]() (рисунок
10,1). В качестве опорных точек используем
10 значений
(рисунок
10,1). В качестве опорных точек используем
10 значений
![]() из
таблицы 1. По графику определим максимальное
по модулю отклонение между функциями
из
таблицы 1. По графику определим максимальное
по модулю отклонение между функциями
![]() и
и
![]() :
:
![]()
Вычислим значение критерия Колмогорова:
![]()
Из таблицы Колмогорова по
заданному уровню значимости
![]() выбираем
критическое значение критерия:
выбираем
критическое значение критерия:
![]()
Так как условие выполняется, гипотеза H0 об экспоненциальном законе распределения принимается (нет оснований ее отклонить).
