
ТВиМС. Пример контрольной работы
..pdf
БГУИР: Дистанционное обучение (неофициальный сайт)
Министерство образования Республики Беларусь Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Факультет заочного и дистанционного обучения Кафедра вычислительных методов и программирования
КОНТРОЛЬНАЯ РАБОТА по дисциплине «Теория вероятностей и математическая статистика»
Проверил: Волковец Александр Иванович
Выполнил: студент группы (дистанционная форма обучения) Wasja
Минск 2009
http://do.ucoz.net
БГУИР: Дистанционное обучение (неофициальный сайт)
1 Задача 1.24
1.1 Условие
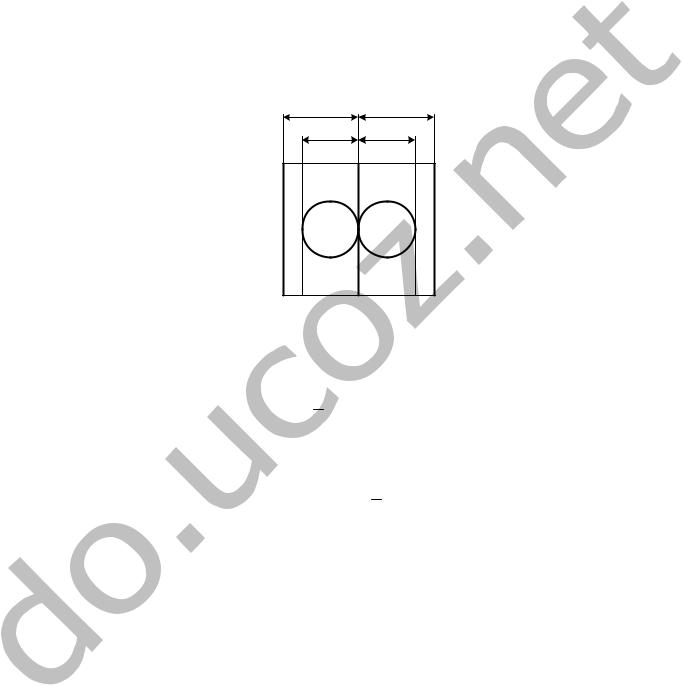
На плоскости проведены параллельные прямые, находящиеся друг от друга на расстоянии 8 см. Определить вероятность того, что наугад брошенный на эту плоскость круг радиусом 3 см не будет пересечен ни одной линией.
1.2 Решение
Часть плоскости, соответствующей условию задачи, выглядит следующим образом:
Рисунок 1.1 – Плоскость
При попадании диска в заштрихованную область диск будет пересекаться линией. Вероятность этого события равна:
P( A) = (6 + 6)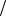 (8 + 8) = 3 / 4
(8 + 8) = 3 / 4
Тогда вероятность того, что диск не будет пересекаться линией:
P( A) = 1 − P( A) = 1 − 3 / 4 = 1/ 4
2 Задача 2.14
2.1 Условие
На рисунке 2.1 приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4. Найти вероятность того, что сигнал пройдет со входа на выход.
http://do.ucoz.net

БГУИР: Дистанционное обучение (неофициальный сайт)
4
3 2.14
1 2
Рисунок 2.1 – Схема соединения
2.2 Решение
Пусть Аi – событие отказа i-го элемента, тогда:
P( A1 ) = p1 = 0,1 ; P( A2 ) = p2 = 0,2 ; P( A3 ) = p3 = 0,3 ; P( A4 ) = p4 = 0,4
При последовательном подключении отказ цепи происходит при отказе хотя бы одного из элементов. Следовательно, часть схемы, состоящая из элементов 1 и 2, выйдет из строя с вероятностью:
P( A1 + A2 ) = P( A1 ) + P( A2 ) - P( A1 × A2 ) = P( A1 ) + P( A2 ) - P( A1 ) × P( A2 ) = 0,1 + 0,2 - 0,1× 0,2 = 0,28
При параллельном подключении отказ цепи происходит при одновременном отказе всех элементов. Следовательно, вероятность отказа заданной схемы составит:
P( A) = P(( A1 + A2 ) × A3 × A4 ) = P( A1 + A2 ) × P( A3 ) × P( A4 ) = 0,28 × 0,3 × 0,4 = 0,0336
Тогда вероятность работоспособности схемы составит:
P( A) = 1 - P( A) = 1 - 0,0336 = 0,9664
3 Задача 3.3
3.1 Условие
Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3 , для второго - 0,5 , для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
3.2 Решение
Пусть событие А – два промаха мимо мишени; H1 – два выстрела первого стрелка; H2 – два выстрела второго стрелка; H3 – два выстрела третьего стрелка.
Тогда с учетом условия:
−вероятность двух промахов первого стрелка:
P( A / H1 ) = (1 - 0,3) × (1 - 0,3) = 0,49 ;
http://do.ucoz.net

БГУИР: Дистанционное обучение (неофициальный сайт)
−вероятность двух промахов второго стрелка:
P( A / H 2 ) = (1 - 0,5) × (1 - 0,5) = 0,25 ;
−вероятность двух промахов третьего стрелка:
P( A / H 3 ) = (1 - 0,8) × (1 - 0,8) = 0,04
Вероятность вызова стрелков равна:
P(H1 ) = P(H 2 ) = P(H 3 ) = 1/ 3
Тогда, поскольку события независимы, по формуле Бейеса вероятность того, что выстрелы произведены первым стрелком:
P(H1 |
/ A) = |
|
|
|
P(H1 ) × P( A / H1 ) |
|
= |
|||
|
|
|
|
|
|
|
||||
|
|
|
P(H1 ) × P( A / H1 ) + P(H 2 ) × P( A / H 2 ) + P(H 3 ) × P( A / H 3 ) |
|||||||
|
= |
|
|
|
(1/ 3) |
× 0,49 |
= |
0,49 |
= 0,628 |
|
|
|
|
× 0,49 |
+ (1/ 3) |
× 0,25 + (1/ 3) × 0,04 |
|
|
|||
|
(1/ 3) |
0,78 |
|
|
||||||
4 Задача 4.24
4.1 Условие
Вероятность попадания в мишень при одном выстреле равна 0,4. По мишени производится шесть независимых выстрелов. Найти вероятность того, что будет хотя бы пять попаданий в мишень.
4.2 Решение
Поскольку каждый выстрел производится независимо от других, то вероятность можно определить по формуле Бернулли.
Тогда, учитывая, что вероятность попадания (p) при выстреле равна 0,4, а вероятность промаха (q) – 0,6:
−вероятность пяти попаданий:
P (5) = C 5 |
× p5 × q 6−5 |
= |
6! |
× 0,4 |
5 |
× 0,61 |
= 6 × 0,01024 × 0,6 = 0,036864 ; |
||
|
|
|
|||||||
6 |
6 |
|
|
5!×(6 |
- 5)! |
|
|
|
|
|
|
|
|
|
|
|
|
||
−вероятность шести попаданий:
P (6) = C 6 |
× p 6 × q 6−6 |
= |
6! |
× 0,4 |
6 |
× 0,60 |
= 1× 0,004096 ×1 = 0,004096 ; |
||
|
|
|
|||||||
6 |
6 |
|
|
6!×(6 |
- 6)! |
|
|
|
|
|
|
|
|
|
|
|
|
||
−вероятность хотя бы пяти попаданий:
http://do.ucoz.net

БГУИР: Дистанционное обучение (неофициальный сайт)
P = P5 (6) + P6 (6) = 0,036864 + 0,004096 = 0,04096
5 Задача 5.28
5.1 Условие
Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таблице). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
p1 |
p2 |
p3 |
p4 |
p5 |
5.28 |
1 |
4 |
5 |
7 |
8 |
0,6 |
0,1 |
0,1 |
0,05 |
0,15 |
5.2 Решение Математическое ожидание дискретной случайной величины Х:
N
M [ X ] = ∑ xi × pi = 1× 0,6 + 4 × 0,1 + 5 ×0,1+ 7 × 0,05 + 8 × 0,15 = 3,05
i=1
Дисперсия дискретной случайной величины Х:
N
D[ X ] = ∑ xi2 × pi - M 2 [ X ] = 12 × 0,6 + 42 × 0,1 + 52 × 0,1 + 72 × 0,05 + 82 × 0,15 - 3,052 =
i=1
= 16,750 - 9,3025 = 7,4475
Функция дискретной величины Х есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений:
F (x) = ∑ p( X = xi )
xi < x
Тогда, исходя из задания:
0 |
|
|
|
|
|
|
|
|
|
|
|
p1 |
|
|
|
|
|
p1 |
+ p2 |
|
|
|
|
F (x) = |
+ p2 |
+ p3 |
|
||
p1 |
|
||||
p |
+ p |
2 |
+ p |
3 |
+ |
1 |
+ p |
+ p |
+ |
||
p |
2 |
3 |
|||
1 |
|
|
|
||
|
x £ x1 , |
0 |
x £ 1, |
|
|
x1 < x £ x2 , |
0,6 |
1 < x £ 4, |
|
|
|
|
|
|
|
x2 |
< x £ x3 , |
0,7 |
4 < x £ 5, |
|
x3 |
< x £ x4 , |
= |
5 < x £ 7, |
|
0,8 |
|||
p4 |
x4 |
< x £ x5 , |
|
7 < x £ 8, |
0,85 |
||||
p4 + p5 |
x > x5 |
|
x > 8 |
|
1 |
||||
График функции распределения будет иметь следующий вид:
http://do.ucoz.net
БГУИР: Дистанционное обучение (неофициальный сайт)
Рисунок 5.1 – График функции распределения
6 Задача 6.1
6.1 Условие
Случайная величина Х задана плотностью вероятности (параметры приведены в таблице):
0, x < a, x > b,
f (x) = ϕ(x, c), a £ x £ b
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал [α ,β ] .
Вариант |
ϕ ( x,c) |
a |
b |
α |
β |
6.1 |
c × x |
1 |
2 |
0,5 |
1,5 |
6.2 Решение
В соответствии с заданием:
|
|
|
0, |
x < 1, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
× x, 1 £ x £ 2, |
|
|
|
|
|
|
|
|
|
||
|
|
|
f (x) = c |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x > 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
Поскольку справедливо равенство ∫ f (x) × dx = 1, то: |
|
|
|
||||||||||||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
∞ |
1 |
2 |
∞ |
|
2 |
C |
× x |
2 |
|
2 |
3 |
×C |
|
2 |
|
|
|
|
|||||||||||||
∫ f (x) × dx = ∫0 × dx + ∫c × x × dx + ∫0 × dx = ∫c × x × dx = |
|
|
|
= |
= 1 C = |
||||||||||
|
2 |
|
|
2 |
|
||||||||||
−∞ |
−∞ |
1 |
2 |
|
1 |
|
|
|
|
1 |
|
3 |
|||
|
|
|
|
|
|
|
|
|
|||||||
Тогда функция плотности вероятности примет вид:
http://do.ucoz.net

БГУИР: Дистанционное обучение (неофициальный сайт)
0, |
x < 1, |
|
|
× x / 3, 1 £ x £ 2, |
|
f (x) = 2 |
||
|
|
x > 2 |
0 |
|
|
Математическое ожидание случайной величины Х:
∞ |
2 |
2 |
2 |
× x |
3 |
|
2 |
|
|||||||
M [ X ] = ∫ x × f (x) × dx = |
× ∫ x2 × dx = |
|
|
|
|||
3 |
|
9 |
|
|
|
||
−∞ |
1 |
|
|
|
1 |
||
|
|
|
|
|
Дисперсия случайной величины Х:
=14 = 1,556
9
∞ |
2 |
|
2 |
|
2 |
2 |
3 |
14 |
|
2 |
2 × x4 |
|
2 |
|
196 |
|
5 |
|
196 |
|
|||
|
|
|
|
|
|
|
|||||||||||||||||
D[ X ] = ∫ x |
|
× f (x) × dx - M |
|
[ X ] = |
|
× ∫ x |
|
× dx - |
|
|
= |
|
|
|
- |
|
|
= |
|
- |
|
|
= 0,080 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
−∞ |
|
|
|
|
3 |
1 |
|
|
9 |
|
|
12 |
|
1 |
|
81 |
|
2 |
|
81 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Функция распределения случайной величины выражается через ее плот-
ность:
−в общем виде:
x
F (x) = ∫ f ( y) × dy
−∞
−на интервале (-∞; 1):
x
F (x) = ∫0 × dy = 0
−∞
− на интервале [1; 2]:
1 |
x |
2 |
-1 |
|
F (x) = ∫0 × dy + ∫(2 × y / 3) × dy = |
x |
|
||
|
3 |
|||
−∞ |
1 |
|
||
|
|
|
||
− на интервале (2; ∞):
1 |
2 |
∞ |
F (x) = ∫0 × dy + ∫(2 × y / 3) × dy + ∫0 × dy = 1
−∞ |
1 |
|
2 |
− окончательная формула: |
|
|
|
0, |
|
x < 1, |
|
|
2 |
-1) / 3, 1 £ x |
£ 2, |
F (x) = (x |
|
||
|
|
x > 2 |
|
1 |
|
|
|
Вероятность попадания случайной величины Х в интервал [0,5; 1,5] равна:
http://do.ucoz.net
БГУИР: Дистанционное обучение (неофициальный сайт) |
|
|
|||||||
|
p(0,5 ≤ x < 1,5) = F (1,5) − F (0,5) = 5 /12 - 0 = 5 /12 |
|
|||||||
7 Задача 7.17 |
|
|
|
|
|
|
|
|
|
7.1 Условие |
|
|
|
|
|
|
|
|
|
Случайная величина Х (условия приведены в таблице) распределена рав- |
|||||||||
номерно на интервале [a,b]. Построить график случайной величины Y=ϕ(X) и оп- |
|||||||||
ределить плотность вероятности g(y). |
|
|
|
|
|
||||
Вариант |
|
ϕ (×) |
|
|
a |
|
|
b |
|
7.17 |
|
|
sin(3x ) |
|
|
π/6 |
|
|
π/3 |
7.2 Решение |
|
|
|
|
|
|
|
|
|
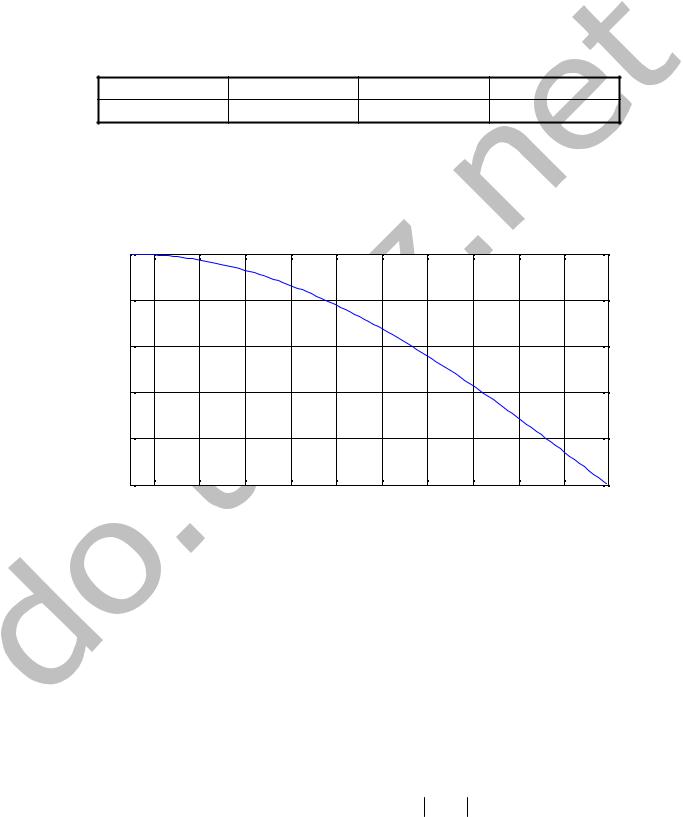
График случайной величины Y = sin(3×x): |
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
0.8 |
|
|
|
|
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
|
|
|
0 |
0.6 |
0.65 |
0.7 |
0.75 |
0.8 |
0.85 |
0.9 |
0.95 |
1 |
0.55 |
|||||||||
|
|
|
|
|
x |
|
|
|
|
|
Рисунок 7.1 – График случайной величины |
|
|||||||
Учитывая равномерность распределения функции на интервале [p/6; p/3], |
|||||||||
плотность ее распределения равна: |
|
|
|
|
|
|
|||
0, |
|
x < π / 6, |
0, |
x < π / 6, |
|
|
-π / 6), |
|
|
/ π , |
π / 6 £ x £ π / 3, |
f (x) = 1/(π / 3 |
π / 6 £ x £ π / 3, = 6 |
||||
0 |
|
x > π / 3 |
0 |
|
x > π / 3 |
|
|
|
|
|
|
Так как функция Y = sin(3×x) дифференцируема и строго убывает, то применима формула:
g ( y ) = f [ψ ( y )]× ψ ¢( y ) ,
http://do.ucoz.net
БГУИР: Дистанционное обучение (неофициальный сайт)
где ψ(y) – функция, обратная заданной функции Y:
ψ ( y ) = arcsin( y ) / 3
Тогда, можно определить производную ψ’(y):
ψ '( y ) = (arcsin( y ))'×1 3 = 1 /(3 ×
3 = 1 /(3 × 
 1 - y 2 )
1 - y 2 )
Интервалу плотности распределения [π/6; π/3] соответствует интервал обратной функции [0; 1]. На этом интервале функция распределения принимает значение f ( x) = 6 / π , поэтому и f [ψ ( y )] = 6 / π . С учетом этого:
g ( y ) = (6 / π ) × (1 /(3 × 
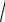 1 - y 2 )) = 2 /(π ×
1 - y 2 )) = 2 /(π × 
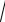 1 - y 2 )
1 - y 2 )
Следовательно, плотность вероятности будет равна:
0, |
|
|
y < 0, |
|
|
|
|
||
|
2 |
|
||
g( y) = |
|
|
|
, 0 £ y £ 1, |
|
|
|
||
π × |
1 - y2 |
|||
|
|
|
y > 1 |
|
0 |
|
|
|
|
8 Задача 8.7
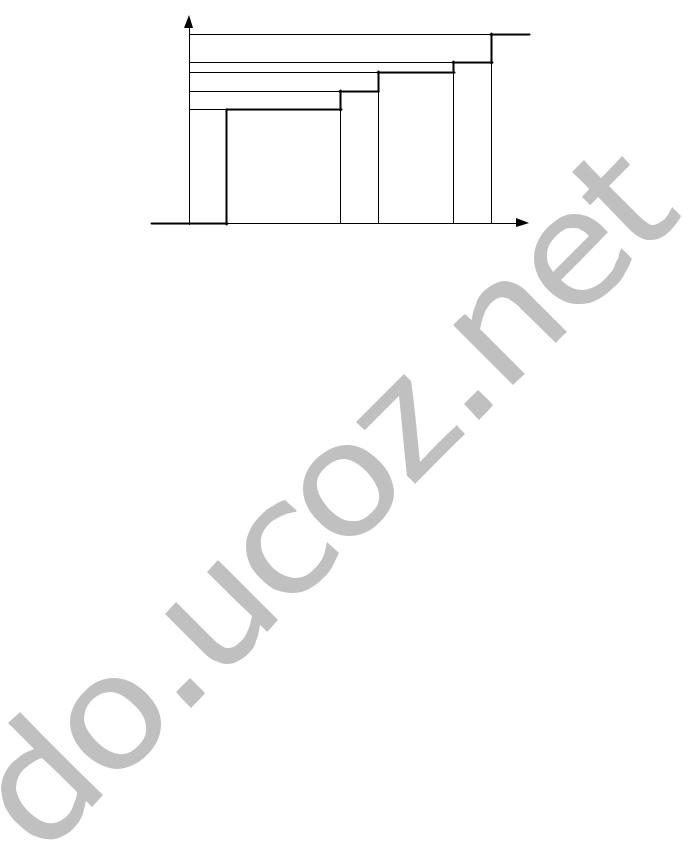
8.1 Условие Двухмерный случайный вектор (Х,У) равномерно распределен внутри вы-
деленной жирными прямыми линиями на рисунке 8.1 области B (конкретные параметры приведены в таблице).
y
y2 
B
y1
x
0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
Рисунок 8.1
http://do.ucoz.net
БГУИР: Дистанционное обучение (неофициальный сайт)
Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
c, (x, y) B, f (x, y) =
0, иначе.
Вычислить коэффициент корреляции между величинами X и Y.
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y1 |
y2 |
8.7 |
2 |
0 |
5 |
4 |
5 |
6 |
1 |
2 |
8.2 Решение
Область B в соответствии с заданием имеет следующий вид:
Рисунок 8.2 |
На основании рисунка можно определить плотность вероятности в аналитической форме:
c, 2 − y ≤ x ≤ 6 − y,0 ≤ y ≤ 2,
f (x, y) =
0 0 ≤ y ≤ 1
Исходя из условия нормировки, можно записать, что:
∞ ∞ |
|
2 |
6− y |
2 |
2 |
1 |
|
∫ ∫ |
f ( x, y) × dx × dy = ∫∫ c × dx × dy = c × ∫ dy ∫ dx = c × ∫ (6 - y - 2 + y) × dy = 4 × c × ∫ dy = 8 × c = 1 c = |
||||||
8 |
|||||||
−∞−∞ |
B |
0 |
2− y |
0 |
0 |
||
|
|||||||
Тогда можно записать:
1/ 8, 2 − y ≤ x ≤ 6 − y,0 ≤ y ≤ 2,
f (x, y) =
0 0 ≤ y ≤ 1
Математические ожидания величин X и Y:
|
∞ ∞ |
1 |
|
1 |
2 |
6− y |
1 |
2 |
24 |
= 3 ; |
|
m X |
= ∫ ∫ x × f ( x, y) ×dx × dy = |
× ∫∫ x × dx × dy = |
× ∫ dy |
∫ x × dx = |
× ∫ (16 - 4 × y) × dy = |
||||||
8 |
8 |
8 |
8 |
||||||||
|
−∞−∞ |
B |
0 |
2− y |
0 |
|
|||||
|
|
|
|
|
|
http://do.ucoz.net
