
Теория вероятностей
.docЗадача 1. Случайные события. Вероятность события (Вариант 21)
Определить вероятность того, что будут вытащены три туза.
Решение.
Вероятность того, что из взятых трех карт все будут тузы
Вероятность того,
что первая карта будет тузом:
![]()
Вероятность того,
что вторая карта будет тузом:
![]()
Вероятность того,
что третья карта будет тузом:
![]()
P=![]() =0.0006
=0.0006
Ответ: P=0.0006
Задача 2. Теоремы сложения и умножения вероятностей (Вариант 14)
В задаче приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q1=0,1; q2=0,2; q3=0,3; q4=0,4; q5=0,5 q6=0,6 . Найти вероятность того, что сигнал пройдет со входа на выход.
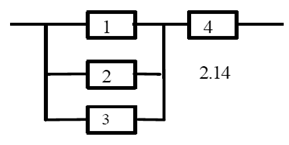
Решение.
Обозначим А – событие состоящее, в том, что сигнал пройдет со входа на выход.
![]() –
событие, состоящее
в том, что i-ый
элемент выйдет из строя
–
событие, состоящее
в том, что i-ый
элемент выйдет из строя
В– сигнал пройдет участок состоящий из элементов 1,2,3.
Рассмотрим
противоположное событие
![]() –
сигнал не пройдет через участок содержащий
элементы 1,2,3.
–
сигнал не пройдет через участок содержащий
элементы 1,2,3.
![]()
Вероятность события
![]()
![]()
Вероятность события В
![]()
Событие А
![]()
Вероятность события А
![]()
Ответ: P(A)=0.5964
Задача 3. Формула полной вероятности. Формула Байеса (Вариант 25)
Прибор состоит из трех блоков. Исправность каждого блока необходима для функционирования устройства. Отказы блоков независимы. Вероятности безотказной работы блоков соответственно равны 0,6; 0,7; 0,8. В результате испытаний один блок вышел из строя. Определить вероятность того, что отказал второй блок.
Решение.
р1=0,6 р2=0,7 р3=0,8
Обозначим А событие состоящее в том, что один блок вышел из строя
Аi – i-ый блок вышел из строя
Можно выдвинуть шесть гипотез:
Н1– отказал один первый блок
Н1=А1![]()
![]()
Н2– отказал один второй блок
Н2=А2![]()
![]()
Н3– отказал один третий блок
Н2=А3![]()
![]()
Н4– отказали два блока
Н4=А1А2![]() +А1
+А1![]() А3+
А3+![]() А2А3
А2А3
Н5– отказали три блока
Н5=А1А2А3
Н6– все блоки работают
Н6=![]()
![]()
![]()
Р(Н1)=(1–р1)р2р3=0,4*0,7*0,8=0,224
Р(Н2)=(1–р2)р1р3=0,6*0,3*0,8=0,144
Р(Н3)=(1–р3)р2р1=0,6*0,7*0,2=0,084
Р(Н4)=(1–р1)(1–р2)р3+(1–р1)(1–р3)р2+(1–р3)(1–р2)р1=0,4*0,3*0,8+0,4*0,7*0,2+0,6*0,3*0,2=0,188
Р(Н5)=(1–р1)(1–р2)(1–р3)=0,4*0,3*0,2=0,024
Р(Н6)=р1р2р3=0,6*0,7*0,8=0,336
Проверка
Р(Н1)+ Р(Н2)+ Р(Н3)+ Р(Н4)+ Р(Н5)+ Р(Н6)=0,224+0,144+0,084+0,188+0,024+0,336=1
Условная вероятность отказа одного блока, если отказал один первый блок
РН1(А)=1
Если отказал один второй блок
РН2(А)=1
Если отказал один третий блок
РН3(А)=1
Если отказали два блока
РН4(А)=0
Если отказали три блока
РН5(А)=0
Если все блоки работают
РН6(А)=0
Вероятность события А найдем по формуле полной вероятности
Р(А)=Р(Н1)* РН1(А)+ Р(Н2)* РН2(А)+ Р(Н3)* РН3(А)+ Р(Н4)* РН4(А) + Р(Н5)* РН5(А)+
+ Р(Н6)* РН6(А)
Р(А)=0,224*1+0,144*1+0,084*1+0,188*0+0,024*0+0,336*0=0,452
Вероятность того, что при поломке одного блока им оказался второй блок найдем по формуле Байеса
РА(Н2)=![]()
Ответ: РА(Н2)=0,3186
Задача 4. Формула Бернулли (Вариант 20)
При установившемся технологическом процессе 90% всей произведенной продукции оказывается продукцией высшего сорта. Сколько изделий должно находиться в ящике, чтобы наивероятнейшее число изделий высшего сорта в ящике составило 340 изделий.
Решение.
р=0,9 К0=340
Наивероятнейшее число изделий высшего сорта найдем по формуле
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Задача 5. Дискретная случайная величина (Вариант 37)
В задаче дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таблице). Найти p отмеченные *. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.
|
Вариант |
x1 |
x2 |
x3 |
x4 |
x5 |
p1 |
p2 |
p3 |
p4 |
p5 |
|
5.37 |
1 |
3 |
5 |
6 |
8 |
0,2 |
0,3 |
0,1 |
* |
0,2 |
Решение.
Найдем вероятность значения Х=6, воспользовавшись свойсвом вероятности
![]()
![]()
Математическое ожидание
М(Х)=![]()
М(Х)=1*0,2+3*0,3+5*0,1+6*0,2+8*0,2 =4,4
Дисперсия
Д(Х)=М(Х2)–( М(Х))2
Где М(Х2)=![]()
М(Х2)= 12*0,2+32*0,3+52*0,1+62*0,2+82*0,2 =22,9
Д(Х)=22,9–4,42=3,54
Функция распределения
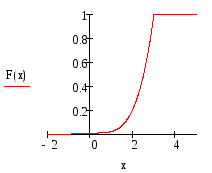
F(xi)=P{X<xi}=P{(X=x1)È(X=x2)È ... È(X=xi-1)}= p1+...+pi-1.
F(X)=
График функции распределения
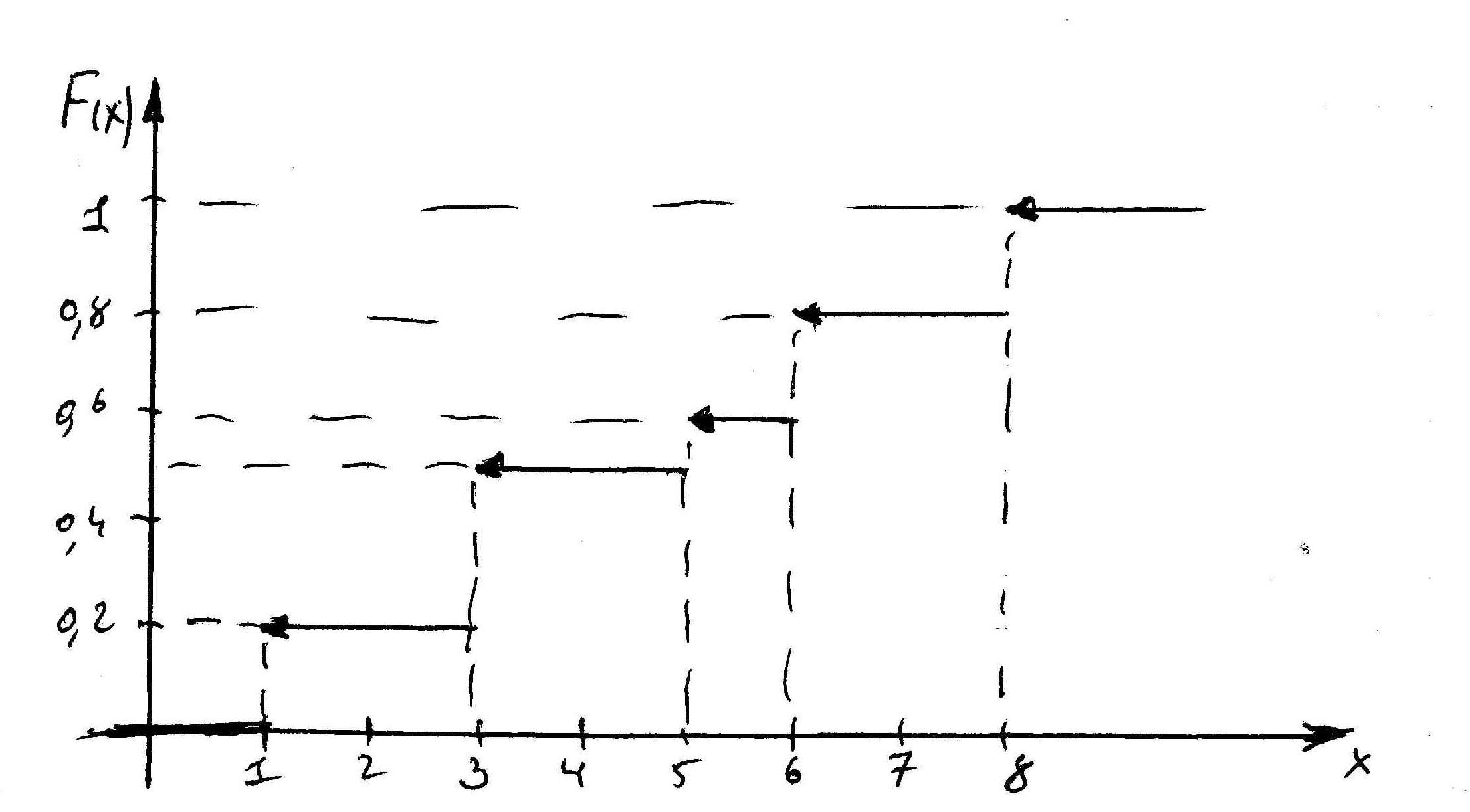
Задача 6. Непрерывная случайная величина (Вариант 4)
В задаче (параметры задания приведены в таблице) случайная величина Х задана плотностью вероятности
![]()
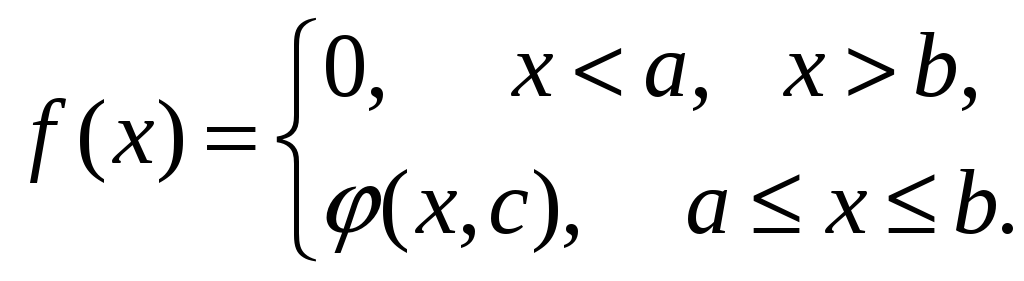
Определить константу
С,
математическое ожидание, дисперсию,
функцию распределения величины Х,
а также вероятность ее попадания в
интервал![]() .
.
|
Вариант |
|
a |
b |
|
|
|
6.4 |
|
-1 |
3 |
-1 |
2 |
Решение.
f(x)=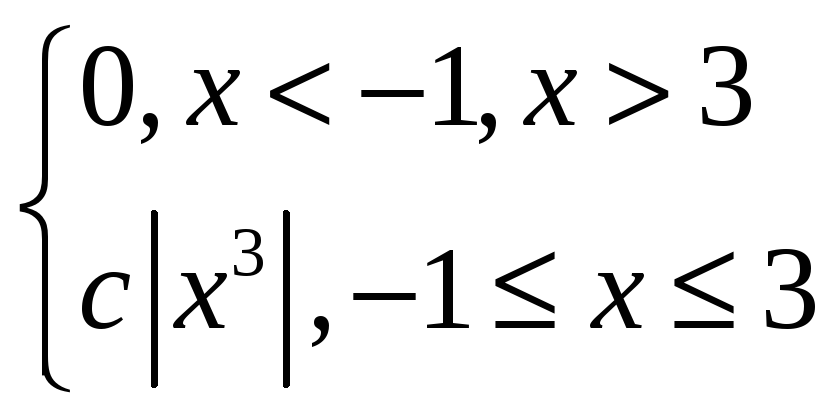
Для определения постоянной с воспользуемся свойством плотности вероятности
![]()
![]()
с=![]()
f(x)=
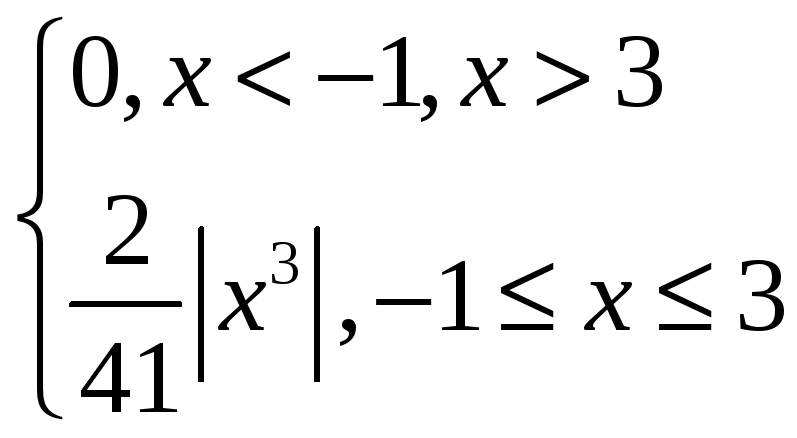
математическое ожидание
М(Х)=![]()
М(Х)=
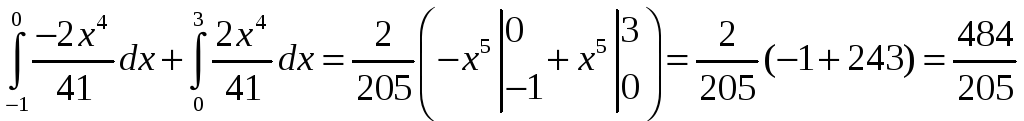
Дисперсия
Д(Х)=М(Х2)–(М(Х))2
Где М(Х2)=
![]()
М(Х2)=
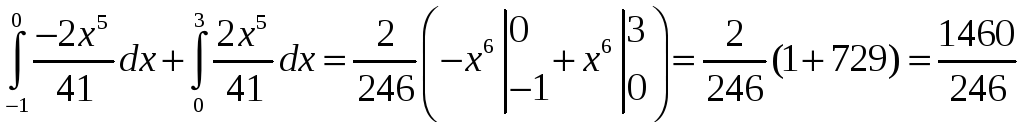
Д(Х)=![]() –(
–(![]() )2=0,3608
)2=0,3608
Вероятность того, что -1<x<2 найдем по формуле
Р(-1<x<2)=

Функция распределения
F(x)=![]()
F(x)=![]() ,x<-1
,x<-1
F(x)=![]() ,-1<x≤0
,-1<x≤0
F(x)=![]() ,0<x≤3
,0<x≤3
F(x)=
![]() ,3<x
,3<x
F(X)=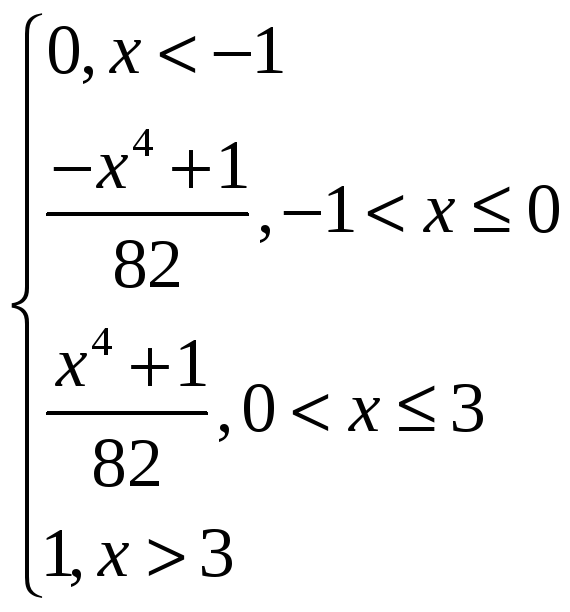
Задача 7. Закон распределения функции случайного аргумента (Вариант 3)
В задаче (условия приведены в таблице) случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).
|
Вариант |
|
a |
b |
|
7.3 |
|
-3 |
2 |
Решение.
Y=![]()
Плотность вероятности СВ Х найдем по формуле
f(x)=![]()
f(x)=1/(2+3)=0,2
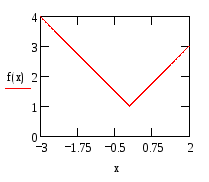
График функции
Y=![]() при
-3≤x≤2
при
-3≤x≤2
x1=1–y х1’=-1
x2=y–1 х2’=1
Так как функция Y отрезке -3≤x≤2 не монотонная, то для нахождения плотности вероятности воспользуемся формулой
g(y)=f(1–y)*(1)+f(y–1)*(1)=0.2+0.2=0.4, 1<y≤3
g(y)=f(1–y)*(1)=0.2+0.2=0.2, 3<y≤4
проверка нормирования
![]()
Ответ: g(y)
=
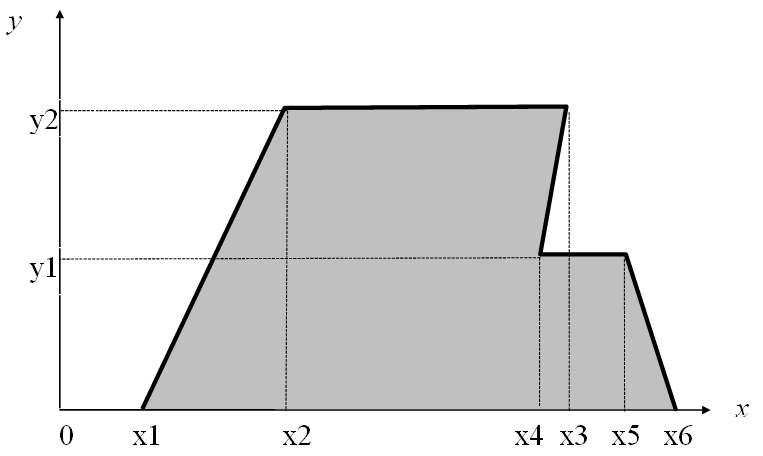
Задача 8. Двухмерные случайные величины (Вариант 37)
В задаче (конкретные параметры приведены в таблице) двухмерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рисунке области B. Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
![]()
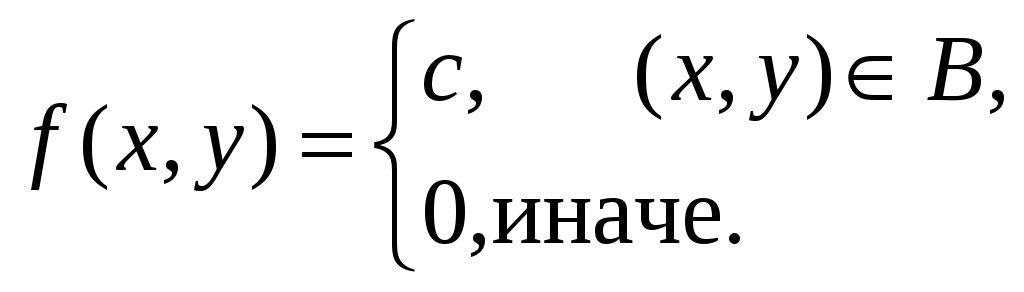
Вычислить коэффициент корреляции между величинами X и Y.
|
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
y1 |
y2 |
|
0 |
0 |
2 |
4 |
4 |
6 |
1 |
2 |
Решение.

y=![]()
Коэффициент корреляции
r=![]()
плотность распределения СВ (x,y) найдем по формуле
f(x,y)=1/S
где S–площадь фигуры
S=0.5*(2+6)*2=8
f(x,y)=![]()
Плотность распределения f(x) найдем по формуле
f(x)=![]()
f(x)=
![]() ,
0<x≤2
,
0<x≤2
f(x)=
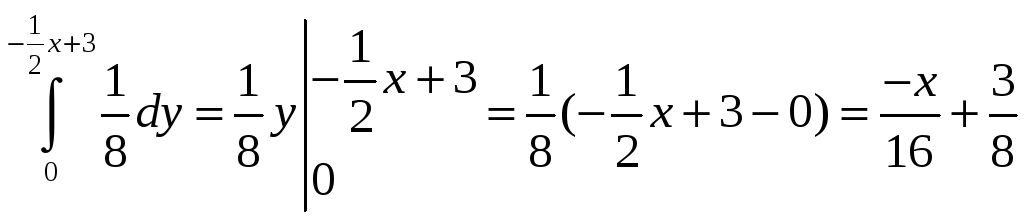 ,
2<x≤6
,
2<x≤6
f(x)=
f(y)=
![]()
f(y)=
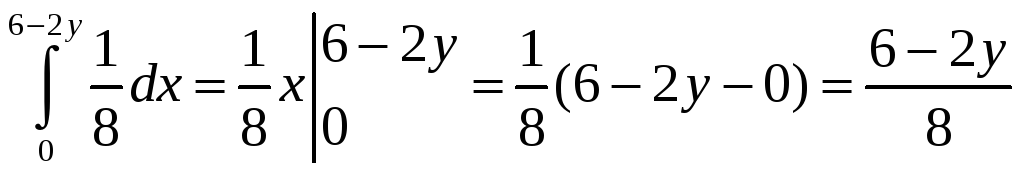 ,0<y≤2
,0<y≤2
f(y)=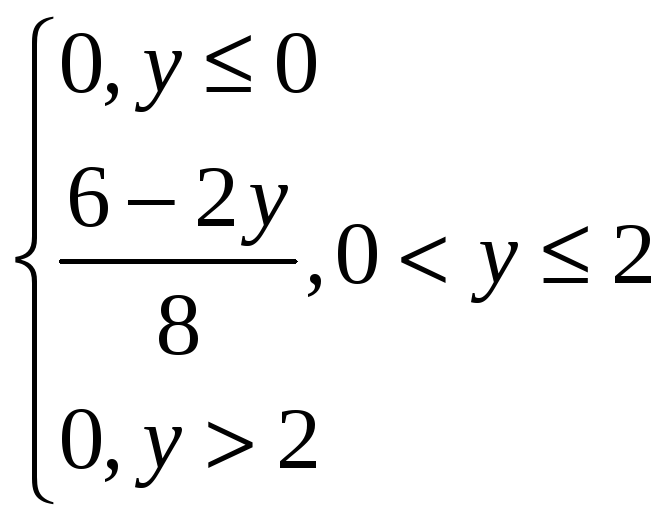
Математическое ожидание
М(Х)=![]()
М(Y)=![]()
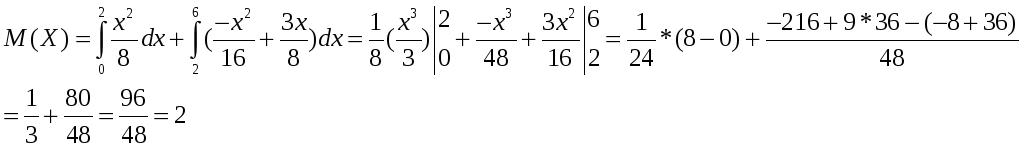
М(Y)=
![]()
К=![]()
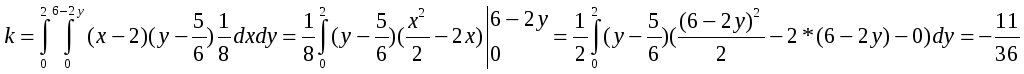
Среднее квадратическое отклонение
![]()
![]()
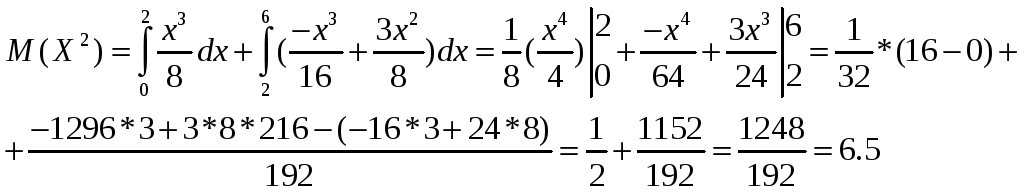
![]()
М(Y2)=
![]()
![]()
r= =-0.3496
=-0.3496
Ответ: r=-0,3496
Задача 9. Числовые характеристики суммы и произведения случайных величин (Вариант 32)
В задаче вычислить
математическое ожидание и дисперсию
величин U
и V,
а так же определить их коэффициент
корреляции
![]() :
:
![]()
![]() .
.
Конкретные значения
коэффициентов
![]() и числовые характеристики случайных
величин
и числовые характеристики случайных
величин
![]() приведены в таблице
приведены в таблице
|
Вариант |
a0 |
a1 |
a2 |
b0 |
b1 |
b2 |
m1 |
m2 |
m3 |
D1 |
D2 |
D3 |
K12 |
K23 |
K13 |
|
9.32 |
3 |
-6 |
4 |
8 |
6 |
8 |
3 |
0 |
6 |
16 |
4 |
1 |
0 |
1 |
2 |
Решение.
Решение:
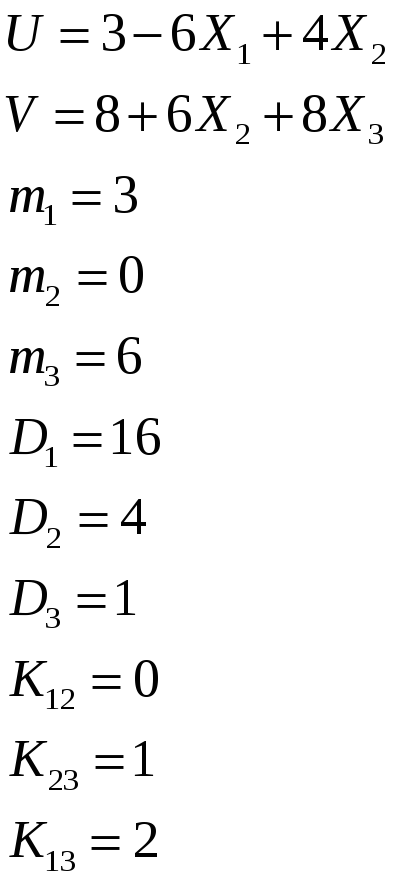
Коэффициент корреляции найдем по формуле
![]()
Воспользуемся свойством математического ожидания
![]()
![]()
Дисперсия
![]()
![]()
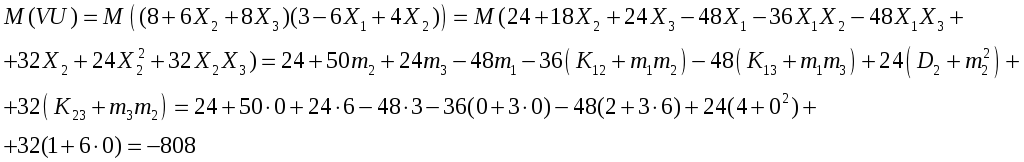
![]()
