ТВиМС- вариант 22

ТВиМС-22

1.12. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает значения от 0 до 9. Найти вероятность того, что все цифры различные и расположены в порядке возрастания (соседние цифры отличаются на 1).

Решение:

Используем классическое определение вероятности: P=m/n, где m - число исходов, благоприятствующих осуществлению события, а n - число всех возможных исходов.

n = 10*9*8*7*6*5 = 151200 способов, так как первую цифру можно выбрать 10 способами (так как всего 10 цифр), вторую - 9, третью - 8 и т.д. Искомая последовательность цифр может быть одна из 9 возможных (предположим, на 0 номер не начинается) m=9.

Получаем P = 9/151200=6*10^-5.

Ответ: P = 6*10^-5

2.26. Приведена схема соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2; p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.

Решение:

Вероятности работы элементов 1, 2, 3, 4, 5 соответственно равны:

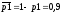
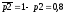
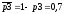
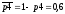
Событие В – безотказная работа цепи.

Событие А1 – безотказная работа части цепи из блоков 1, 2, 3, А2 – из блоков 4, 5.

Найдем вероятность работы для части ветви цепи:

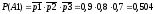
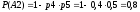
Вероятность того, что сигнал пройдет с входа на выход:

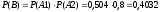
Ответ:

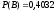
3.29. Три стрелка производят по одному выстрелу по одной и той же мишени. Вероятность попадания для первого стрелка равна 0,6 , для второго - 0,5 , для третьего - 0,4. В результате произведенных выстрелов в мишени оказалось две пробоины. Найти вероятность того, что в мишень попал второй стрелок.

Решение:

Событие А – в мишень попали 2 стрелка. Гипотеза Н1 – второй стрелок попал, Н2 – второй не попал.

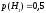
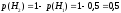
Найдем условную вероятность 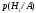, т.е. вероятность того, что в мишень попал второй стрелок и либо первый, либо третий. Эти 2 события несовместны, поэтому применима теорема сложения:

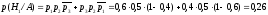
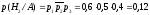
Искомая вероятность того, что попал второй стрелок по формуле Байеса равна:

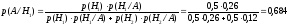
Ответ: 0,684

4.4. Игральную кость подбрасывают 12 раз. Чему равно наивероятнейшее число выпадений 6?

Решение:

Найдем наивероятнейшее число выпадения 6:

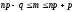
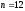
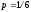
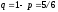
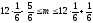
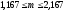
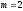
Ответ:

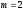
5.19. Дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

xi	-2	0	2	4	9
pi	0,15	0,15	0,2	0,4	0,1

Решение:

Функцию распределения определим по формуле:

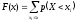
- для ,

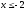
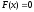- для ,

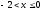
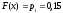- для ,

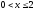
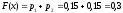- для ,

- для ,

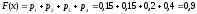- для ,

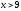
x	≤-2	]-2;0]	]0;2]	]2;4]	]4;9]	>9
F(x)	0	0,15	0,3	0,5	0,9	1

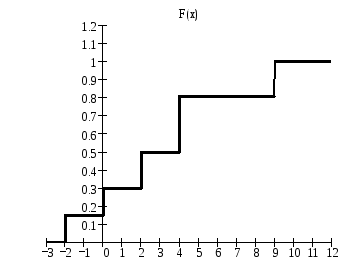
Математическое ожидание характеризует среднее значение СВ и определяется по формуле:

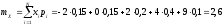
Дисперсия случайной величины характеризует степень рассеивания (разброса) значений случайной величины относительно ее математического ожидания и определяется по формуле:

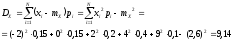
Ответ: , .

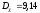6.7. Cлучайная величина Х задана плотностью вероятности

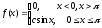
Определить константу , математическое ожидание, дисперсию, функцию распределения величины , а также вероятность ее попадания в интервал .

Решение:

Константу вычислим исходя из условия нормировки:

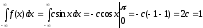
откуда .

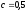Так как плотность вероятности задана различными формулами на разных интервалах, то и функцию распределения будем искать для каждого интервала в отдельности.

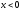ё

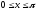
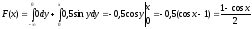
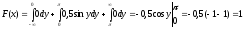
Окончательно имеем

Вероятность попадания в интервал :

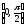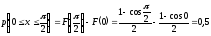
Математическое ожидание:

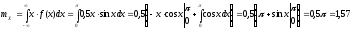
Дисперсиия:

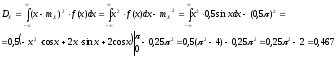
Ответ: , , , , .

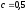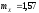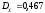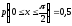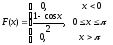7.28. Случайная величина Х распределена равномерно на интервале . Построить график случайной величины и определить плотность вероятности g(y).

Решение:

Так как Х равномерно распределена в интервале -1, 4, то ее плотность вероятности равна:

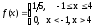
Построим график величины 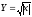для x в интервале 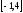и в зависимости от числа k обратных функций выделим следующие интервалы для Y:

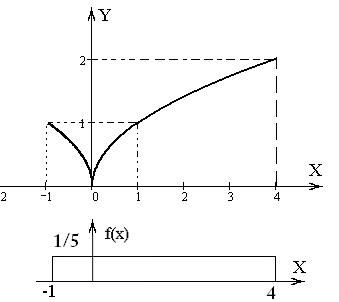
[-, 0[ k = 0,

[0, 1] k = 2,

]1, 2] k = 1,

]2, +] k = 0.

Так как на интервалах [-, 0 [ и ]2, +] обратная функция не существует, то для этих интервалов g(y)=0.

В интервале [0,1] две обратных функци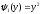и:

и

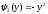
Плотность вероятности 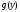величины Y определяем по формуле:

В интервале ]1,2] одна обратная функция 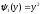, следовательно:

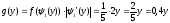
Таким образом, плотность вероятности величины Y равна

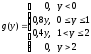
Ответ:

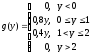
8.16. Двумерный случайный вектор (Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. области B. Двумерная плотность вероятности f(x,y) одинакова для любой точки этой области B:

Вычислить коэффициент корреляции между величинами X и Y.

Решение:

9. По выборке одномерной случайной величины:

- получить вариационный ряд;

- построить на масштабно-координатной бумаге формата А4 график эмпирической функции распределения F^*(x);

- построить гистограмму равноинтервальным способом;

- построить гистограмму равновероятностным способом;

- вычислить оценки математического ожидания и дисперсии;

- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи критерия согласия ² и критерия Колмогорова ( = 0,05).

Одномерная выборка:

3.86 2.22 -5.61 -6.08 -0.63-10.31 0.25 -2.32 0.81 -9.90 -0.81 -2.84 -3.34 -5.71 -2.85-11.09 -6.47 -6.02 -2.47 -6.82 -7.55-11.08 -6.44 -5.98 -0.61 -0.52 -6.30 -9.63 -1.98 -2.98 -0.32 -3.10 -1.16 -6.11 -7.32 -1.23 -7.22 -2.04 -5.70 -1.80 -7.28 -6.87 -2.28 -3.81 -2.04-13.50 -7.11 -7.54-11.10 -5.23 -7.29 -4.32 -5.30-13.69 -3.84 -2.62 -5.04 -9.41 -5.61 -3.97 1.77-12.05 -9.31 -4.33 -5.63 -8.83 -4.57-10.01 0.67 -2.97 -7.70 -9.83 -5.70 -6.06 -1.58 -1.48 -2.33 -4.72 -4.70 -3.54 -1.07 0.67 -2.80 -3.00 3.01 -1.50 -6.24 -1.30 -3.79 -3.19 -8.48 -4.53 -3.91 -1.28 -5.60 -3.41 -9.98 1.22 2.32 1.17

График эмпирической функции распределения F^*(x):

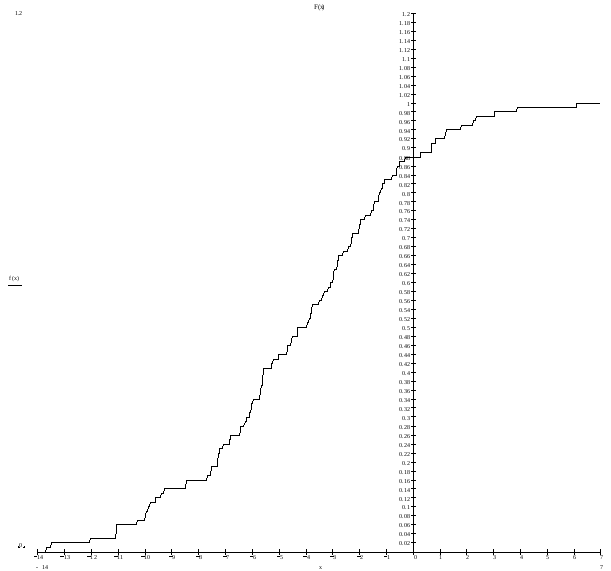
Гистограмма равноинтервальным способом

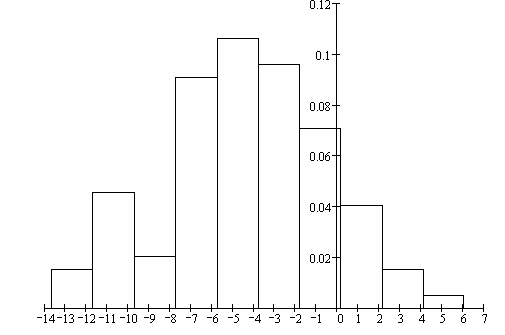
Гистограмма равновероятностным способом

Несмещенная состоятельная оценка математического ожидания, называемая выборочным средним, вычисляется по формуле

Несмещенная состоятельная оценка дисперсии равна

По виду гистограмм выдвигаем гипотезу о том, что случайная величина X распределена по нормальному закону:

H₀ : ,;

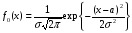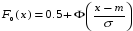H₁ : f(x)  N(m, ).

Используя метод моментов определим оценки неизвестных параметров m и σ гипотетического (нормального) закона распределения:

,

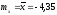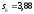
Значение критерия вычисляем по формуле :

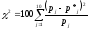
При проверке гипотезы используем равновероятностную гистограмму. В этом случае

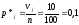
Теоретические вероятности p_i рассчитываем по формуле:

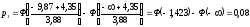
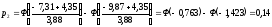
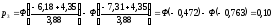
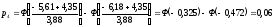
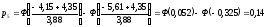
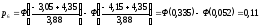
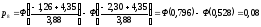
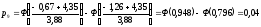
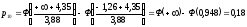
После этого проверяем выполнение контрольного соотношения

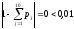
Тогда

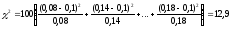
После этого из таблицы распределения ² выбираем критическое значение 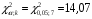. Так как 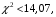то гипотеза H₀ принимается (нет основания ее отклонить).

Теоретическая функция распределения F₀(x) равномерного закона R(0,5;5,25) равна

.

Максимальная разность по модулю между графиками F*(x) и F₀(x)

Z = 0,36 при х = 1,16.

Вычислим значение критерия Колмогорова

Из таблицы Колмогорова выбираем критическое значение Так как  < 1,36 , то гипотеза о равномерном законе распределения принимается.

10. По выборке двумерной случайной величины:

- вычислить оценку коэффициента корреляции;

- вычислить параметры линии регрессии a₀ и a₁;

- построить диаграмму рассеивания и линию регрессии.

Двумерная выборка:

( 8.96; 11.91) ( 5.24; 5.22) ( 7.32; 10.74) ( 9.08; 8.05) ( 2.38; 3.88) ( 5.23; 5.90) ( 7.76; 9.68) ( 1.61; -1.53)

( 0.50; 3.73) ( 8.93; 6.54) ( 10.00; 6.28) ( 2.11; 4.53) ( 0.94; 4.60) ( 3.61; 6.85) ( 10.50; 8.96) ( 7.71; 5.00)

( 5.23; 8.13) ( 6.49; 7.14) ( 2.80; 4.08) ( 4.04; 3.97) ( 3.86; 5.91) ( 5.31; 3.86) ( 5.18; 4.78) ( 6.21; 6.94)

( 0.37; 3.85) ( 3.37; 3.05) ( 1.12; 3.74) ( 1.08; 6.46) ( 9.24; 4.99) ( -0.72; 0.21) ( 7.52; 4.64) ( 3.95; 8.19)

( 0.83; 4.78) ( 5.57; 6.58) ( 1.26; 3.16) ( 5.82; 0.84) ( 5.62; 4.08) ( 1.33; 5.97) ( 5.46; 8.09) ( 1.05; 4.82) ( 0.82; -1.72) ( 7.01; 9.68) ( 8.22; 6.76) ( 6.89; 9.31) ( 3.23; 6.06) ( 9.24; 5.42) ( 7.99; 10.31) ( 5.47; 6.24) ( 2.45; 0.67) ( 5.65; 7.73)