Контрольная работа № 1. Теория вероятностей

Выполнил:

Задача № 1.32

В урне 6 белых и 7 черных шаров. Из урны вынимают шар – отмечается его цвет и он возвращается в урну, после этого вынимают второй шар. Найти вероятность того, что шары будут белые.

Решение:

Обозначим: событие А - появление двух белых шаров. Событие А представляет собой произведение двух событий:

А=

где - появление белого шара при первом вытаскивании ( из 13 шаров);

- появление белого шара при втором вытаскивании (тоже из 13 шаров, т.к. первый шар мы кладём обратно).

По теореме умножения вероятностей

Ответ: P(A)=0,213.

Задача № 2.6

В задачах 2.1-2.40 приведены схемы соединения элементов, образующих цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны q₁=0,1; q₂=0,2; q₃=0,3; q₄=0,4; q₅=0,5 q₆=0,6 . Найти вероятность того, что сигнал пройдет со входа на выход.

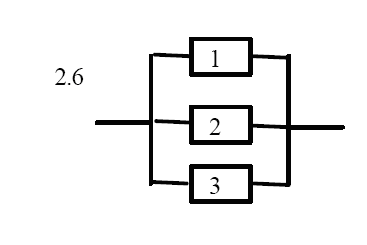
Решение:

Пусть P – вероятность прохождения сигнала со входа на выход

Поскольку события отказа элементов в совокупности независимы, то общая формула для вероятности P запишется следующим образом:

Ответ: P=99,4%.

Задача 3.25

Прибор состоит из трех блоков. Исправность каждого блока необходима для функционирования устройства. Отказы блоков независимы. Вероятности безотказной работы блоков соответственно равны 0,6; 0,7; 0,8. Определить вероятность того, что отказал второй блок.

Решение:

Можно сделать следующие предположения:

- отказал 1-ый блок, 2-ой и 3-ий исправны. Вероятность данного события:

- отказал 2-ой блок, 1-ый и 3-ий исправны. Вероятность данного события:

- отказал 3-ий блок, 2-ой и 1-ый исправны. Вероятность данного события:

Так как известно, что отказал один блок, очевидно, что условные вероятности остальных гипотез равны нулю.

Событие достоверно при гипотезах , следовательно соответствующие условные вероятности равны единице:

По формуле полной вероятности, вероятность того, что откажет один блок:

По формуле Бейеса, искомая вероятность того, что отказал 3-ий блок, равна:

Ответ:

Задача 4.7

Рабочий обслуживает десять однотипных станков. Вероятность того, что станок потребует внимания рабочего в течение часа, равна 0,05. Найти вероятность того, что в течение часа этих требований будет от трех до пяти.

Решение:

- Формула Бернулли

p=0,05

q=1-0,05=0,95

P=P₁₀(3)+ P₁₀(4)+ P₁₀(5)

P=P₁₀(3)+ P₁₀(4)+ P₁₀(5)==0,01132

Ответ:P=0,01132.

Задача 5.25

В задачах 5.1-5.40 дискретная случайная величина Х может принимать одно из пяти фиксированных значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения приведены в таб. 5.1). Найти p отмеченные *. Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и построить график функции распределения.

Вариант	x1	x2	x3	x4	x5	p1	p2	p3	p4	p5
5.25	2	4	6	8	10	0,1	0,2	0,3	0,35	0,05

Решение:

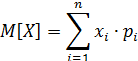
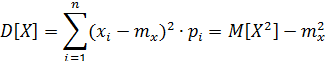
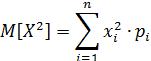
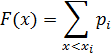
F(x=2)=0

F(x=4)=0,1

F(x=6)=0,1+0,2=0,3

F(x=8)=0,1+0,2+0,3=0,6

F(x=10)=0,1+0,2+0,3+0,35=0,95

F(x>10)=1

Ответ:; .

Задача 6.24

В задачах 6.1-6.40 (параметры заданий приведены в табл. 6.1) случайная величина Х задана плотностью вероятности

Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х, а также вероятность ее попадания в интервал.

Вариант	x,c)	A	b		
6.24		1	4	1	2,5

Решение:

1)Вычислим константу исходя из условия нормировки:

Отсюда константа :

2. Определим математическое ожидание СВ Х:

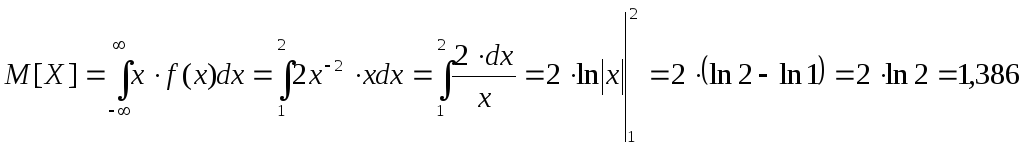
2. Определим дисперсию СВ Х:

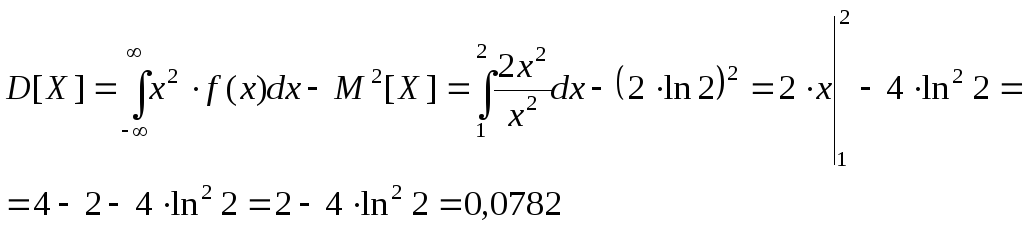
2. Определим функцию распределения величины Х:

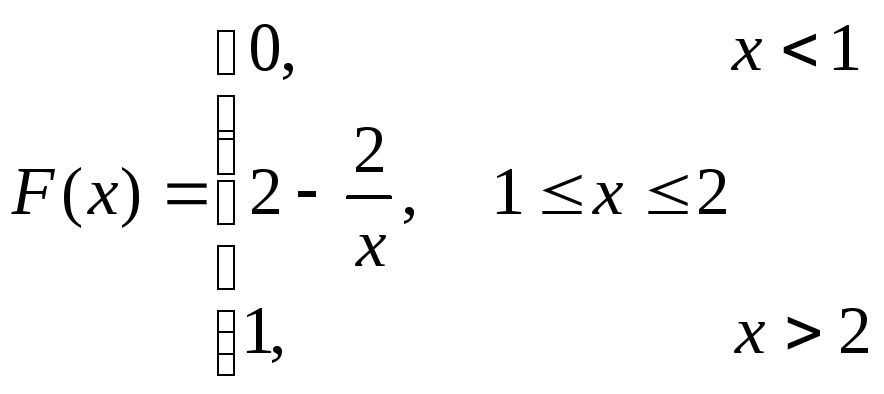
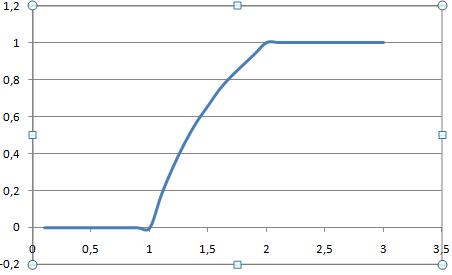
2. Определим вероятность попадания величины Х в заданный интервал :

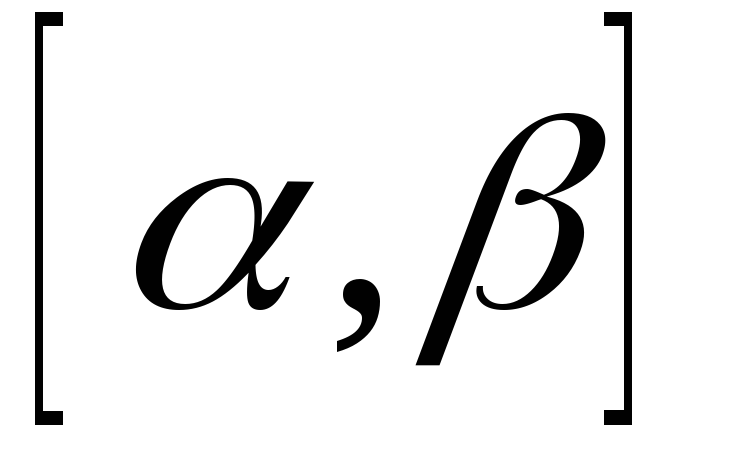Ответ:

Задача 7.32

В задачах 7.1-7.40 (условия приведены в табл. 7.1) случайная величина Х распределена равномерно на интервале [a,b]. Построить график случайной величины Y=(X) и определить плотность вероятности g(y).

Вариант		a	B
7.32		-1	2

Решение:

1. Построим график случайной величины 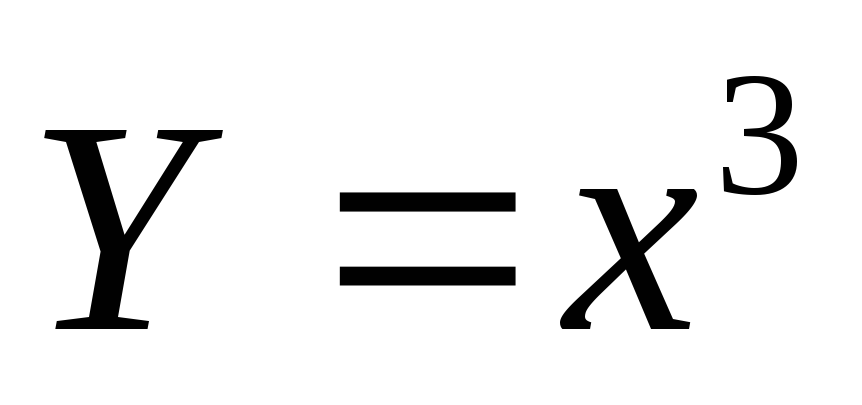для в интервале значений и определим диапазон значений :.

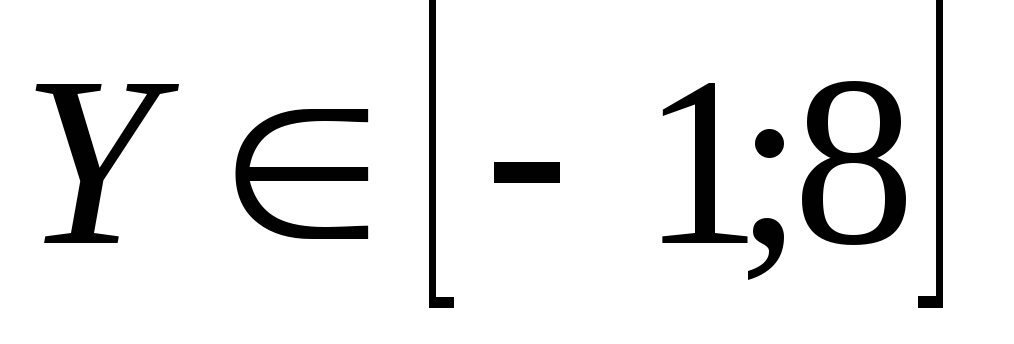2. В зависимости от числа обратных функций выделим следующие интервалы для :

обратных функций не существует

обратных функций не существует

3) Вычислим модули производных обратных функций:

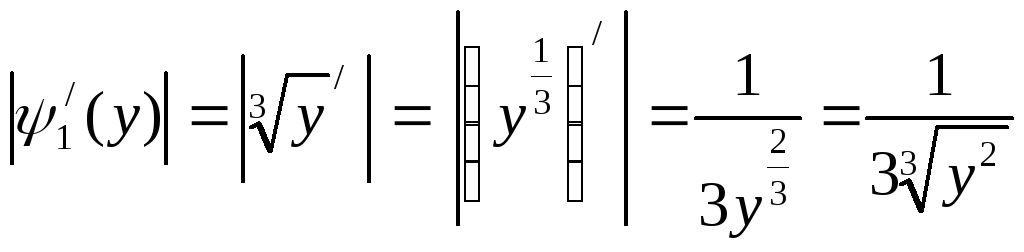
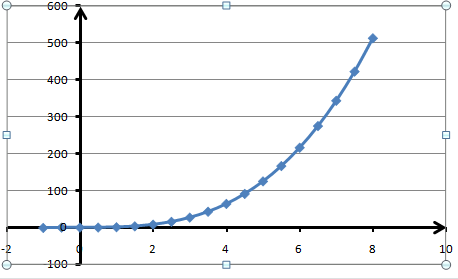
Рис. 7.1 – график функции x³

Т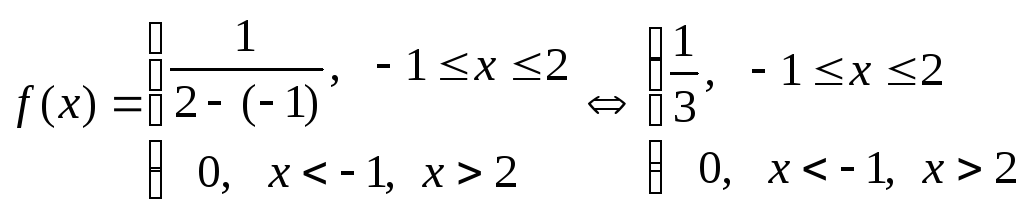ак как случайная величина Х распределена равномерно на интервале [-1;2] , то её плотность вероятности равна:

4. Определим плотность вероятности величины :

Ответ: