- •Глава 1. Элементы теории функции комплексного переменного
- •Комплексные числа и действия над ними
- •Упражнения
- •Упражнения для самостоятельной работы
- •2. Множества точек, линии, области на комплексной плоскости
- •Упражнения
- •Упражнения для самостоятельной работы
- •3. Функции комплексного переменного. Предел. Непрерывность функции. Основные элементарные функции
- •1. Дробно - рациональная функция
- •Упражнения для самостоятельной работы
- •4. Производная функции комплексного переменного. Условия дифференцируемости. Аналитические функции. Понятие о конформном отображении
- •Упражнения
- •Упражнения для самостоятельной работы
- •5. Интегрирование функции комплексного переменного
- •5.1. Интеграл от функции комплексного переменного
- •5.2. Вычисление интеграла от аналитической функции
- •5.3. Интегральная формула Коши
- •Упражнения
- •Упражнения для самостоятельной работы
- •6. Ряды в комплексной области
- •6.1. Ряды с комплексными членами Ряд
- •6.2. Ряды Тейлора и Лорана
- •Упражнения
- •Упражнения для самостоятельной работы
- •7. Изолированные особые точки функции комплексного переменного
- •7.1. Классификация изолированных особых точек
- •7.2. Ряды и особые точки
- •7.3. Нули аналитической функции. Связь между нулем и полюсом
- •7.4. Особенности функции в бесконечно удаленной точке
- •Точка называется существенно особой для функции, еслине существует.
- •Упражнения
- •Упражнения для самостоятельной работы
- •8. Вычеты и их применение к вычислению контурных интегралов
- •8.1. Вычет функции и его вычисление
- •8.2. Теоремы о вычетах и их применение к вычислению контурных интегралов
- •Упражнения
- •Упражнения для самостоятельной работы
- •8.3. Применение вычетов к вычислению определенных и несобственных интегралов
- •Упражнения для самостоятельной работы
- •Упражнения для самостоятельной работы
Упражнения для самостоятельной работы
62. Выяснить, дифференцируемы ли следующие функции. В случае дифференцируемости найти производную:
а)
![]() :
б)
:
б)![]() в)
в)![]() ; г)
; г)![]() .
.
63. Выяснить, какие из следующих функций являются аналитическими хотя бы в одной точке, а какие – нет:
а)
![]() :
б)
:
б)![]() в)
в)![]() .
.
64.
Показать, что условия Коши-Римана в
полярных координатах имеют вид
![]() ,
и проверить выполнение этих условий
для функций: а)
,
и проверить выполнение этих условий
для функций: а)![]() :
б)
:
б)![]() .
Являются ли эти функции аналитическими
и где?
.
Являются ли эти функции аналитическими
и где?
65.
Найти аналитическую функцию в области
![]() по действительной или мнимой части:
по действительной или мнимой части:
а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
66.
Найти коэффициент подобия
![]() и угол поворота
и угол поворота![]() при отображении с помощью функции
при отображении с помощью функции![]() в точках:
в точках:
а)
![]() б)
б)![]() .
.
67.
Найти коэффициент подобия и угол поворота
при отображении в данной точке
![]()
а)
![]() б)
б)![]() .
.
68.
Выяснить, какая часть комплексной
плоскости растягивается, а какая –
сжимается при отображении с помощью
функции
![]() .
.
69. Является ли конформным отображение:
а)
![]() , б)
, б)![]() ; в)
; в)![]() .
.
5. Интегрирование функции комплексного переменного
5.1. Интеграл от функции комплексного переменного
Пусть
в области
![]() плоскости
плоскости![]() задана однозначная непрерывная функция
задана однозначная непрерывная функция![]() и пусть
и пусть![]() кусочно-гладкая
направленная кривая, принадлежащая
кусочно-гладкая
направленная кривая, принадлежащая![]() вместе со своими концами
вместе со своими концами![]() и
и![]() .
.
По определению полагают
 ,
(5.1)
,
(5.1)
где
![]() произвольная
точка элементарной дуги
произвольная
точка элементарной дуги![]() при произвольном разбиении дуги
при произвольном разбиении дуги![]() на
на![]() частей точками
частей точками![]() .
.
При
данных условиях интеграл от функции
![]() вдоль кривой
вдоль кривой![]() ,
как предел интегральной суммы (5.1),
существует.
,
как предел интегральной суммы (5.1),
существует.
Вычисление интеграла от функции комплексного переменного сводится к вычислению двух криволинейных интегралов 2-го рода по формуле
![]() .
(5.2)
.
(5.2)
Из формулы (5.2) следует, что на интегралы от функции комплексного переменного распространяются известные свойства криволинейных интегралов.
Если
кривая задана параметрическими
уравнениями
![]() ,
что равносильно одному уравнению в
комплексной форме
,
что равносильно одному уравнению в
комплексной форме![]()
![]() ,
то имеет место удобная для вычисления
интеграла формула
,
то имеет место удобная для вычисления
интеграла формула
![]() (5.3)
(5.3)
5.2. Вычисление интеграла от аналитической функции
Интеграл
![]() ,
вообще говоря, зависит от пути
интегрирования. Условием независимости
интеграла от пути интегрирования
является аналитичность подынтегральной
функции.
,
вообще говоря, зависит от пути
интегрирования. Условием независимости
интеграла от пути интегрирования
является аналитичность подынтегральной
функции.
Важную роль в теории функций комплексного переменного играет интегральная теорема Коши. Приведем две формулировки теоремы для одно- и многосвязной областей.
Пусть
![]() кусочно-гладкая
замкнутая кривая, будем ее называть
замкнутым контуром.
кусочно-гладкая
замкнутая кривая, будем ее называть
замкнутым контуром.
Теорема
Коши (для односвязной области).
Пусть функция
![]() аналитична в односвязной области
аналитична в односвязной области![]() ,
тогда для любого замкнутого контура
,
тогда для любого замкнутого контура![]() (рис.5.1) имеет место равенство
(рис.5.1) имеет место равенство
![]() .
(5.4)
.
(5.4)
Теорема
Коши (для многосвязной области).
Пусть
![]() аналитична в многосвязной области
аналитична в многосвязной области![]() ,
ограниченной внешним контуром
,
ограниченной внешним контуром![]() и внутренними контурами
и внутренними контурами![]() .
Тогда имеет место равенство
.
Тогда имеет место равенство
![]()
![]() (5.5)
(5.5)
при условии, что интегрирование по всем контурам производится против часовой стрелки (рис.5.2).
Как
следствие последней теоремы (для
двусвязной области) следует отметить
утверждение: если
![]() аналитична в области
аналитична в области![]() всюду, кроме
всюду, кроме![]() ,
то
,
то
![]() ,
(5.6)
,
(5.6)
где
![]() и
и![]() произвольные
контуры в
произвольные
контуры в![]() ,
содержащие особую точку
,
содержащие особую точку![]() (рис.5.3).
(рис.5.3).
|
Рис.5.1 |
Рис.5.2 |
Для аналитической функции имеет место формула Ньютона-Лейбница
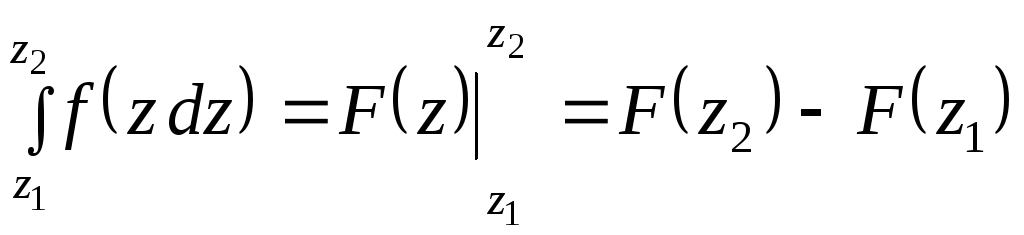 ,
(5.7)
,
(5.7)
где
![]() первообразная
для
первообразная
для![]() ,
т.е.
,
т.е.![]() .
Этой формулой можно пользоваться для
вычисления интеграла вдоль пути, лежащего
в односвязной области, где
.
Этой формулой можно пользоваться для
вычисления интеграла вдоль пути, лежащего
в односвязной области, где![]() аналитична,
если известна первообразная для
аналитична,
если известна первообразная для![]() .
.
|
Рис.5.3
|
Техника нахождения неопределенных интегралов в комплексном анализе та же, что и в действительном, таблица основных интегралов в обоих случаях одинакова.
|