- •Глава 1. Элементы теории функции комплексного переменного
- •Комплексные числа и действия над ними
- •Упражнения
- •Упражнения для самостоятельной работы
- •2. Множества точек, линии, области на комплексной плоскости
- •Упражнения
- •Упражнения для самостоятельной работы
- •3. Функции комплексного переменного. Предел. Непрерывность функции. Основные элементарные функции
- •1. Дробно - рациональная функция
- •Упражнения для самостоятельной работы
- •4. Производная функции комплексного переменного. Условия дифференцируемости. Аналитические функции. Понятие о конформном отображении
- •Упражнения
- •Упражнения для самостоятельной работы
- •5. Интегрирование функции комплексного переменного
- •5.1. Интеграл от функции комплексного переменного
- •5.2. Вычисление интеграла от аналитической функции
- •5.3. Интегральная формула Коши
- •Упражнения
- •Упражнения для самостоятельной работы
- •6. Ряды в комплексной области
- •6.1. Ряды с комплексными членами Ряд
- •6.2. Ряды Тейлора и Лорана
- •Упражнения
- •Упражнения для самостоятельной работы
- •7. Изолированные особые точки функции комплексного переменного
- •7.1. Классификация изолированных особых точек
- •7.2. Ряды и особые точки
- •7.3. Нули аналитической функции. Связь между нулем и полюсом
- •7.4. Особенности функции в бесконечно удаленной точке
- •Точка называется существенно особой для функции, еслине существует.
- •Упражнения
- •Упражнения для самостоятельной работы
- •8. Вычеты и их применение к вычислению контурных интегралов
- •8.1. Вычет функции и его вычисление
- •8.2. Теоремы о вычетах и их применение к вычислению контурных интегралов
- •Упражнения
- •Упражнения для самостоятельной работы
- •8.3. Применение вычетов к вычислению определенных и несобственных интегралов
- •Упражнения для самостоятельной работы
- •Упражнения для самостоятельной работы
Упражнения для самостоятельной работы
48. Найти значение функции в указанной точке, записав число в алгебраической форме.
|
а)
|
б)
|
|
в)
|
г)
|
49. Найти значения степеней:
а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
50.
Решить уравнение
![]() .
.
51.
Доказать тождество:
![]() ;
;![]() ;
;![]() .
.
52.
При отображении
![]() найти:
найти:
а)
образ линии
![]()
![]() ;
;
б)
образ области
![]()
![]() ,
,![]() .
.
53.
При отображении
![]() найти:
найти:
а) образы прямых, параллельных действительной оси;
б)
образ прямоугольника:
![]()
![]() .
.
54.
Найти область
![]() ,
в которую преобразуется область
,
в которую преобразуется область![]() :
:![]() ,
,![]() ,
,![]() при помощи функции
при помощи функции![]() .
.
4. Производная функции комплексного переменного. Условия дифференцируемости. Аналитические функции. Понятие о конформном отображении
Пусть
однозначная функция
![]() определена в некоторой области
определена в некоторой области![]() и пусть точки
и пусть точки![]() и
и![]() принадлежат области
принадлежат области![]() .
.
Определение.
Если
существует конечный предел отношения
![]() ,
когда
,
когда![]() по любому закону стремится к нулю, то:
по любому закону стремится к нулю, то:
этот предел называется производной функции
 в точке
в точке
 и обозначается символом
и обозначается символом
![]() ;
(4.1)
;
(4.1)
2)
в этом случае функция
![]() называетсядифференцируемой
в точке
называетсядифференцируемой
в точке
![]() .
.
Все правила и формулы дифференцирования функции действительного переменного остаются в силе и для функций комплексного переменного.
Теорема.
Для того,
чтобы функция
![]() была дифференцируема в точке
была дифференцируема в точке![]() ,
необходимо и достаточно, чтобы:
,
необходимо и достаточно, чтобы:
1)
действительные функции
![]() и
и![]() были дифференцируемы в точке
были дифференцируемы в точке![]() )
;
)
;
в этой точке выполнялись условия
![]() ,
(4.2)
,
(4.2)
называемые условиями Коши-Римана (C.-R.) или Даламбера-Эйлера.
При выполнении условий (C.-R.) производная функции может быть найдена по одной из следующих формул:
![]() (4.3)
(4.3)
Приведем два определения, имеющих фундаментальное значение в теории функции комплексного переменного.
Определение. Функция называется аналитической в области, если она дифференцируема в каждой точке этой области.
Определение.
Функция
называется
аналитической
в точке
![]() ,
если она является аналитической в
некоторой окрестности точки
,
если она является аналитической в
некоторой окрестности точки![]() ,
т.е. если функция дифференцируема не
только в данной точке, но и в ее окрестности.
,
т.е. если функция дифференцируема не
только в данной точке, но и в ее окрестности.
Из приведенных определений видно, что понятия аналитичности и дифференцируемости функции в области совпадают, а аналитичность функции в точке и дифференцируемость в точке – разные понятия. Если функция аналитична в точке, то она, безусловно, дифференцируема в ней, но обратное может и не иметь места. Функция может быть дифференцируема в точке, но не быть дифференцируемой ни в какой окрестности этой точки, в таком случае она не будет аналитической в рассматриваемой точке.
Условием аналитичности функции в области является выполнимость условий Коши–Римана для всех точек этой области.
Связь
аналитических функций с гармоническими.
Любая ли функция двух переменных
![]() и
и![]() может
служить действительной и мнимой частью
некоторой аналитической функции?
может
служить действительной и мнимой частью
некоторой аналитической функции?
Если
функция
![]() аналитическая в области
аналитическая в области![]() ,
то функции
,
то функции![]() и
и![]() являются гармоническими, т.е удовлетворяют
уравнению Лапласа.
являются гармоническими, т.е удовлетворяют
уравнению Лапласа.
![]() и
и
![]() .
.
Однако
если функции
![]() и
и![]() являются произвольно выбранными
гармоническими функциями, то функция
являются произвольно выбранными
гармоническими функциями, то функция![]() ,
вообще говоря, не будет аналитической,
т.е. условия
,
вообще говоря, не будет аналитической,
т.е. условия![]() для
них не всегда будут выполняться.
для
них не всегда будут выполняться.
Можно
построить аналитическую функцию
![]() по одной заданной гармонической функции
(например,
по одной заданной гармонической функции
(например,![]() ),
подобрав другую
),
подобрав другую![]() так, чтобы удовлетворялись условия
так, чтобы удовлетворялись условия![]() .
Условия
.
Условия![]() (4.2) позволяют определить неизвестную
функцию (например,
(4.2) позволяют определить неизвестную
функцию (например,![]() ) по ее двум частным производным или,
что то же самое, по ее полному дифференциалу.
Отыскивание гармонической функции по
ее дифференциалу есть известная из
действительного анализа задача
интегрирования полного дифференциала
функции двух переменных.
) по ее двум частным производным или,
что то же самое, по ее полному дифференциалу.
Отыскивание гармонической функции по
ее дифференциалу есть известная из
действительного анализа задача
интегрирования полного дифференциала
функции двух переменных.
Геометрический
смысл модуля и аргумента производной.
Пусть функция
![]() дифференцируема в области
дифференцируема в области![]() и
и![]() .
Функция отобразит точку
.
Функция отобразит точку![]() плоскости
плоскости![]() в точку
в точку![]() плоскости
плоскости![]() ,
кривую
,
кривую![]() ,
проходящую через точку
,
проходящую через точку![]() в
кривую
в
кривую![]() ,
проходящую через
,
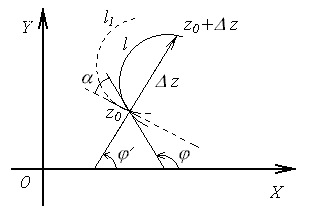
проходящую через![]() (рис.4.1).
(рис.4.1).
Модуль
производной
![]() есть предел отношения бесконечно малого
расстояния между отображенными точками
есть предел отношения бесконечно малого
расстояния между отображенными точками![]() и
и![]() к бесконечно малому расстоянию между
их прообразами
к бесконечно малому расстоянию между
их прообразами![]() и
и![]() .
Поэтому величину
.
Поэтому величину![]() можно рассматривать геометрически как
коэффициент растяжения (если
можно рассматривать геометрически как
коэффициент растяжения (если![]() )
в точке
)
в точке![]() при отображении области
при отображении области![]() в области
в области![]() ,
осуществляемом функцией
,
осуществляемом функцией![]()
|
|
|
Рис. 4.1
В
каждой точке области в каждом направлении
коэффициент растяжения
![]() будет свой. Для аргумента производной
можно записать
будет свой. Для аргумента производной
можно записать
![]()
![]() ,
,
где
![]() и
и![]() это
соответственно углы
это
соответственно углы![]() и
и![]() ,
которые векторы
,
которые векторы![]() и
и![]() образуют с действительной осью (рис.4.1).
Пусть
образуют с действительной осью (рис.4.1).
Пусть![]() и
и![]() углы, образованные касательными к кривой
углы, образованные касательными к кривой![]() и
и![]() в точках
в точках![]() и
и![]() с действительной осью. Тогда при
с действительной осью. Тогда при![]()
![]() ,
а
,
а![]() ,
поэтому
,
поэтому![]() определяет угол, на который нужно
повернуть касательную к кривой
определяет угол, на который нужно
повернуть касательную к кривой![]() в точке
в точке![]() ,
чтобы получить направление к касательной
к кривой
,
чтобы получить направление к касательной
к кривой![]() в точке
в точке![]() .
.
Если
рассмотреть две кривые
![]() и
и![]() ,
,![]() и
и![]() ,
то углы
,
то углы![]() и
и![]() (рис. 4.1) между их касательными, вообще
говоря, неравные.
(рис. 4.1) между их касательными, вообще
говоря, неравные.
Определение.
Отображение
области
![]() на область
на область![]() ,
обладающее свойствами постоянства
растяжений (
,
обладающее свойствами постоянства
растяжений (![]() )
в любом направлении и сохранения (или
консерватизма) углов
)
в любом направлении и сохранения (или
консерватизма) углов![]() между двумя кривыми, пересекающимися
в точке
между двумя кривыми, пересекающимися
в точке![]() ,
называетсяконформным
(подобным в
малом). Отображение, осуществляемое
аналитической функцией, является
конформным во всех точках, в которых
,
называетсяконформным
(подобным в
малом). Отображение, осуществляемое
аналитической функцией, является
конформным во всех точках, в которых
![]() .
.