
- •Глава 1. Элементы теории функции комплексного переменного
- •Комплексные числа и действия над ними
- •Упражнения
- •Упражнения для самостоятельной работы
- •2. Множества точек, линии, области на комплексной плоскости
- •Упражнения
- •Упражнения для самостоятельной работы
- •3. Функции комплексного переменного. Предел. Непрерывность функции. Основные элементарные функции
- •1. Дробно - рациональная функция
- •Упражнения для самостоятельной работы
- •4. Производная функции комплексного переменного. Условия дифференцируемости. Аналитические функции. Понятие о конформном отображении
- •Упражнения
- •Упражнения для самостоятельной работы
- •5. Интегрирование функции комплексного переменного
- •5.1. Интеграл от функции комплексного переменного
- •5.2. Вычисление интеграла от аналитической функции
- •5.3. Интегральная формула Коши
- •Упражнения
- •Упражнения для самостоятельной работы
- •6. Ряды в комплексной области
- •6.1. Ряды с комплексными членами Ряд
- •6.2. Ряды Тейлора и Лорана
- •Упражнения
- •Упражнения для самостоятельной работы
- •7. Изолированные особые точки функции комплексного переменного
- •7.1. Классификация изолированных особых точек
- •7.2. Ряды и особые точки
- •7.3. Нули аналитической функции. Связь между нулем и полюсом
- •7.4. Особенности функции в бесконечно удаленной точке
- •Точка называется существенно особой для функции, еслине существует.
- •Упражнения
- •Упражнения для самостоятельной работы
- •8. Вычеты и их применение к вычислению контурных интегралов
- •8.1. Вычет функции и его вычисление
- •8.2. Теоремы о вычетах и их применение к вычислению контурных интегралов
- •Упражнения
- •Упражнения для самостоятельной работы
- •8.3. Применение вычетов к вычислению определенных и несобственных интегралов
- •Упражнения для самостоятельной работы
- •Упражнения для самостоятельной работы
Упражнения
Написать в комплексной форме уравнение кривой
 :
:
![]() .
.
Решение.
1-й способ.
Согласно (2.1) имеем параметрическое
уравнение кривой
![]() .
.
2-й
способ. Легко
видеть, что данная кривая – парабола
![]() .
Перейдем в этом уравнении к комплексному
переменному, воспользовавшись
.
Перейдем в этом уравнении к комплексному
переменному, воспользовавшись
формулами
(2.2),
![]() ,
откуда получаем
,
откуда получаем
![]() .
.
Написать уравнение окружности в комплексной форме.
Решение.
1-й способ. Рассмотрим
окружность как множество точек
![]() ,
равноудаленных на расстояние
,
равноудаленных на расстояние![]() от центра
от центра![]() .
Тогда имеем
.
Тогда имеем![]() .
.
2-й
способ. Как
известно, параметрические уравнения
окружности радиуса
![]() с
центром в точке
с
центром в точке![]() имеют вид
имеют вид
![]() где
где
![]() .
.
Следовательно,
![]()
![]() .
Если воспользоваться показательной
формой комплексного числа, то полученное
уравнение можно записать в виде
.
Если воспользоваться показательной
формой комплексного числа, то полученное
уравнение можно записать в виде![]()
![]() .
.
Написать уравнение эллипса с фокусами в точках
 и
и ,
большая ось которого равна
,
большая ось которого равна .
.
|
Рис.2.1 |
Решение.
По определению эллипса
|
Расстояние
между фокусами:
![]() ,
а малая полуось по известным
,
а малая полуось по известным![]() и
и![]() определяется из формулы
определяется из формулы![]() .
.
Выяснить геометрический смысл уравнения
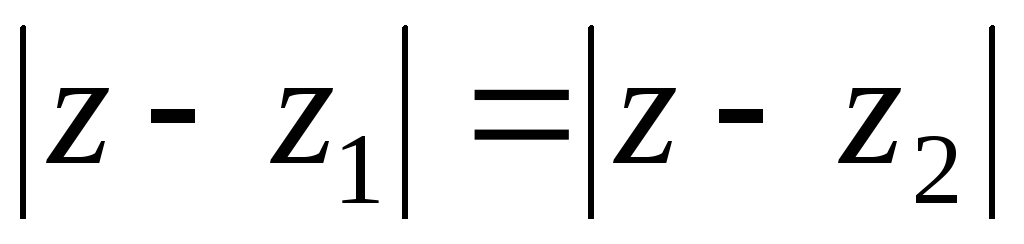 .
.
|
Рис.2.2 |
Решение.
1-й способ
геометрический. В
данном случае
|
2-й
способ аналитический.
Пусть
![]()
![]() ,
тогда
,
тогда
![]()
![]()
![]()
![]() .
.
Поскольку
левые части последних соотношений
равны, то равны и их правые части, т.е.
![]() .
После упрощения получаем уравнение
прямой линии.
.
После упрощения получаем уравнение
прямой линии.
Какая кривая определяется уравнением
 ?
?
Решение.
Из области определения функции исключается
точка
![]() ,
пусть
,
пусть![]() .
Тогда
.
Тогда![]() .
Следовательно,
.
Следовательно,![]() .
По условию
.
По условию![]() или
или![]() ,
откуда следует, что данное условие
определяет окружность
,
откуда следует, что данное условие
определяет окружность![]() ,
,![]() .
.
Определить, какое множество точек удовлетворяет условию
 .
.
|
|
Решение.
Так как по определению
|
26. Построить на комплексной плоскости области, заданные условиями:
а)
![]() ; б)
; б)![]() ,
,![]() .
.
Решение.
а) Искомое множество точек удовлетворяет
двум неравенствам:
![]() и
и![]() .
Первое условие определяет точку эллипса
с фокусами
.
Первое условие определяет точку эллипса
с фокусами![]() и
и![]() ,
для которого
,
для которого![]() ,
,![]() ,
,![]() (уравнение эллипса в действительных
переменных:
(уравнение эллипса в действительных
переменных:![]() ).
Второе уравнение – внутренность эллипса
с фокусами в тех же точках с полуосями
).
Второе уравнение – внутренность эллипса
с фокусами в тех же точках с полуосями![]() и
и![]() (уравнение эллипса в действительных
переменных
(уравнение эллипса в действительных
переменных![]() ).
).
|
Рис.2.4 |
Искомое множество точек – часть плоскости, заключенная между двумя эллипсами (рис. 2.4), включая сами эллипсы. |
б)
Легко видеть, что множество точек,
удовлетворяющих условию
![]() ,
есть внутренность кольца, ограниченного
окружностями
,
есть внутренность кольца, ограниченного
окружностями![]() и
и![]() с центрами в начале координат и радиусами
1 и 2. Система неравенств
с центрами в начале координат и радиусами
1 и 2. Система неравенств![]() определяет множество точек, составляющих
угол между лучами
определяет множество точек, составляющих
угол между лучами![]() и
и![]() ,
причем точки первого луча принадлежат
области, а второго – нет.
,
причем точки первого луча принадлежат
области, а второго – нет.
Пересечение
указанных множеств определяет искомую
область
![]() ,
которая изображена на рис. 2.5.
,
которая изображена на рис. 2.5.
27.
Какое множество точек комплексной
плоскости определяется условием
![]() ?
?
Решение.
Пусть
![]() .
Тогда
.
Тогда![]() и
и![]() .
Следовательно,
.
Следовательно,![]() .
По условию
.
По условию![]() или
или![]() .
Полученное неравенство определяет
множество точек, изображенных на рис.
2.6.
.
Полученное неравенство определяет
множество точек, изображенных на рис.
2.6.
|
Рис.2.5 |
Рис.2.6 |

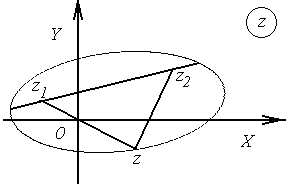

 Рис.2.3
Рис.2.3

