
Комплексні числа
Нехай
![]() -
множина все можливих впорядкованих пар
-
множина все можливих впорядкованих пар
![]() дійсних чисел
дійсних чисел
![]() .
Множина
з введеними на ній операціями додаванням
й множенням
.
Множина
з введеними на ній операціями додаванням
й множенням
![]() утворює поле, яке називається полем
комплексних чисел.
утворює поле, яке називається полем
комплексних чисел.
Введемо позначення
![]() .
Тоді
.
Тоді
![]() ,
або
,
або
![]() .
.
Впорядковану пару
дійсних чисел
називають комплексним число і
записують у вигляді
![]() .
.
Запис
![]() -
алгебраїчна форма комплексного числа
-
алгебраїчна форма комплексного числа
![]() .
Дійсне число
називається дійсною частиною
z і позначається
.
Дійсне число
називається дійсною частиною
z і позначається
![]() .
Дійсне число
називається уявною частиною
z і позначається
.
Дійсне число
називається уявною частиною
z і позначається
![]() ,
,
![]() -
уявна одиниця.
-
уявна одиниця.
Нехай
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
Комплексне число
![]() називається комплексно спряженим
до числа z і позначається
називається комплексно спряженим
до числа z і позначається
![]() .
.
Мають місце
наступні|слідуючі|
властивості, що легко перевіряються,
для будь-яких
![]() :
:
1.
![]() ;
;
2.
Число z буде дійсним тоді і лише
тоді, коли
![]() ;
;
3.
Число
![]() завжди дійсне і невідємне;
завжди дійсне і невідємне;
4.
![]() ;
;
Приклад 1.28. Добути квадратній корінь з комплексного числа.
Розв’язання. Нехай
-
довільне комплексне число. Припустимо,
що квадратній корінь з нього існує та
дорівнює
![]() ,
тобто
,
тобто
![]() .
Тоді
.
Тоді
![]() ,
або
,
або
![]() .
Визначимо тепер
.
Визначимо тепер
![]() і
і
![]() :
:
![]() або
або
![]() .
.
Звідси випливає,
що
![]() ;
;
![]() .
.
Для знаходження
![]() значення
,
заданими цими формулами, не можна
комбінувати довільно, оскільки згідно
з формулою
значення
,
заданими цими формулами, не можна
комбінувати довільно, оскільки згідно
з формулою
![]() знак добутку
знак добутку
![]() має збігатися зі знаком числа
.
має збігатися зі знаком числа
.
Приклад1.29.
Розв’язати квадратне рівняння
![]() .
.
Розв’язання. Обчислимо
![]() ,
,
а
також
![]() .
Нехай
.
Нехай
![]() .
Тоді за формулами для
і
з попереднього прикладу
.
Тоді за формулами для
і
з попереднього прикладу
![]() ;
;
![]() .
.
Таким чином,
![]() або
або
![]() .
.
Отже,
![]() ;
;
![]() .
.
Комплексне число
зображується точкою
![]() площини, або вектором
площини, або вектором
![]() ,
який виходить із початку координат, а
кінець цього вектора є точка
.
,
який виходить із початку координат, а
кінець цього вектора є точка
.
Довжина
![]() радіуса-вектора називається модулем
комплексного числа
радіуса-вектора називається модулем
комплексного числа
![]() ,
а кут
,
а кут
![]() ,
утворений радіусом-вектором з додатнім
напрямом даної осі – аргументом
цього числа
,
утворений радіусом-вектором з додатнім
напрямом даної осі – аргументом
цього числа
![]() .
Очевидно, що
.
Очевидно, що
![]() ,
,
а визначити з рівностей
![]() ;
;
![]() ,
,
але (у зв’язку з
періодичністю
![]() і
і
![]() )
не однозначно, а з точністю до доданків,
кратних до
)
не однозначно, а з точністю до доданків,
кратних до
![]() .
.
Подаючи комплексне
число у тригонометричній формі
![]() аргумент
беремо в межах
аргумент
беремо в межах
![]() .
.
Зауважимо, що для визначення потрібно використати обидві формули, оскільки значення тільки однієї тригонометричної функції не дає змоги визначити, в якій чверті лежить шуканий кут.
При переході від алгебраїчної форми комплексного числа до тригонометричної доцільно спочатку зобразити дане число відрізком координатної площини. Це полегшує знаходження значення аргументу.
Нехай
![]() ;
;
![]() .
.
Тоді
![]() ;
;
![]() ;
;
![]() -
формула Муавра.
-
формула Муавра.
![]() де
де
![]() .
.
Приклад 1.30. Знайти
геометричне місце точок, що зображають
комплексні числа
,
які задовольняють умови:
![]() ;
;
![]() .
.
Розв’язання.
Нехай
![]() ,
тоді
,
тоді
![]() ,
або
,
або
![]() .
Звідси
.
Звідси
![]() .
А цю умову задовольняють, як відомо, усі
точки круга з центром у точці
.
А цю умову задовольняють, як відомо, усі
точки круга з центром у точці
![]() і радіусом 3 /рис.1.1/.
і радіусом 3 /рис.1.1/.
Заштрихована фігура і є зображенням усіх комплексних чисел, які задовольняють задані умови.
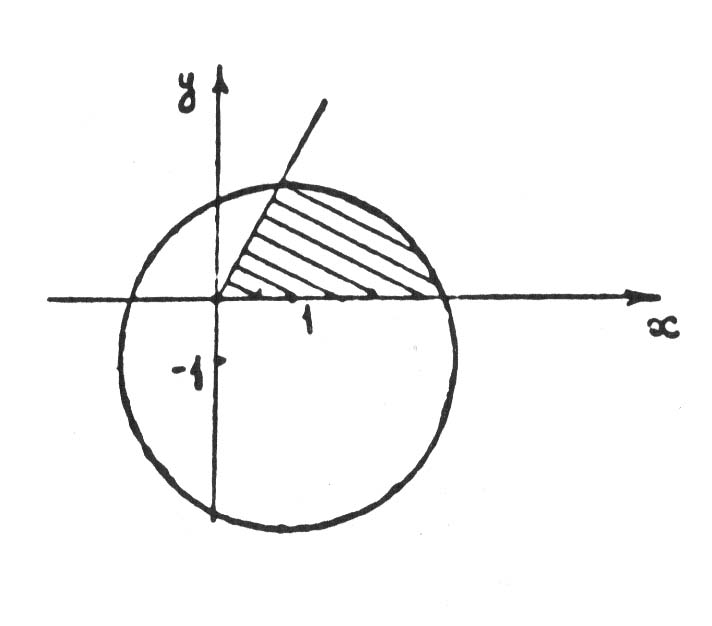
Рис.1.1
Приклад 1.31.
Обчислити
![]()
Розв’язання.
Подамо числа
![]() ;
;
![]() в тригонометричній формі:
в тригонометричній формі:
![]() ;
;
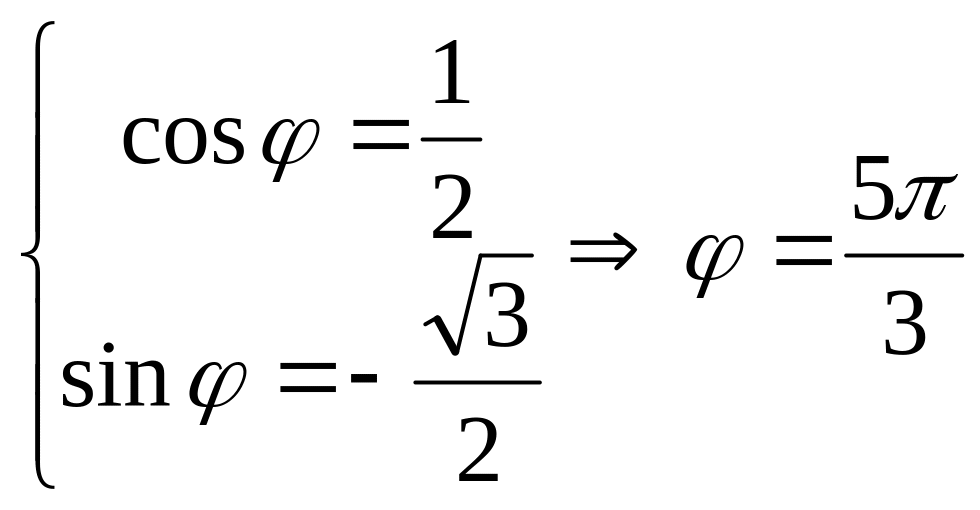 ;
;
![]() ;
;
![]() ;
;
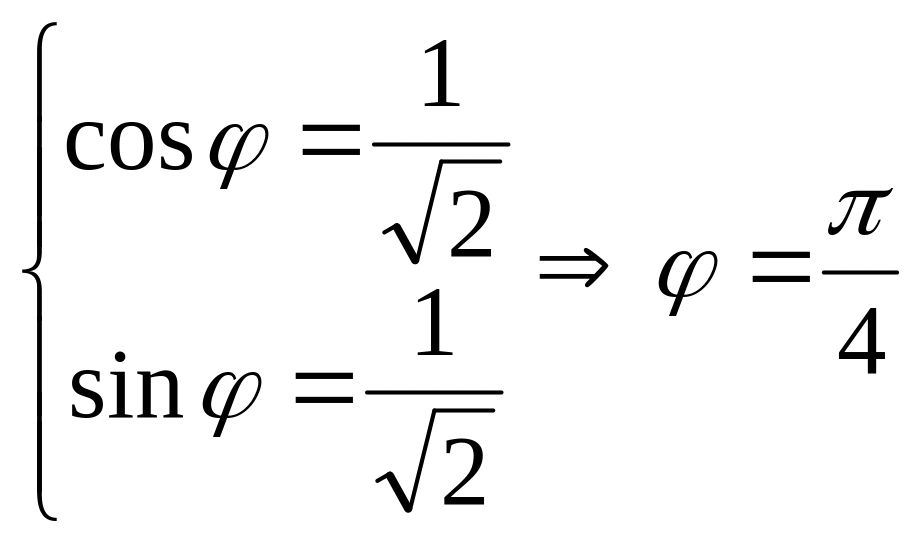 ;
;
![]() ;
;
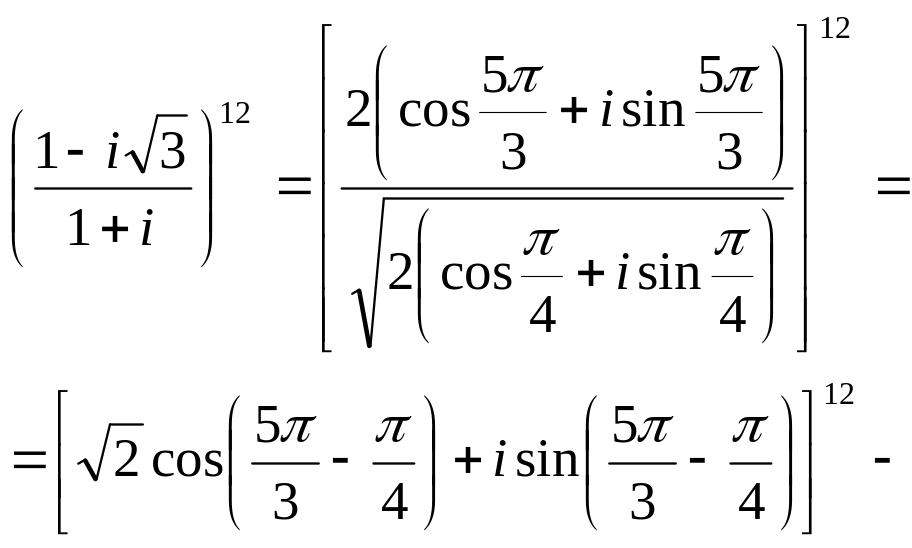
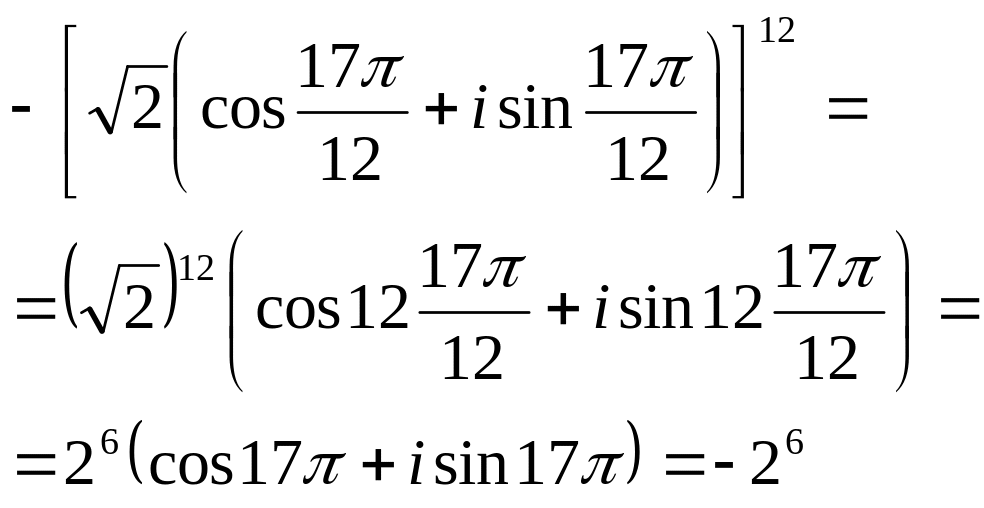
Приклад 1.32.
Обчислити
![]()
Розв’язання.
Тригонометрична форма числа
![]() має вигляд
має вигляд
![]() .
Тоді за формулою добування кореня
-го
степеня з комплексного числа, маємо
.
Тоді за формулою добування кореня
-го
степеня з комплексного числа, маємо
![]() ,
де
,
де
![]() ,
,
звідки
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Іншою часто використовуваною формою представлення комплексних чисел, є їх експоненціальна форма, яка виходить перетворенням тригонометричної форми за формулою Ейлера:
![]() .
.
У цьому випадку з
![]() випливає, що
випливає, що
![]() .
.
Використання експоненціальної форми запису комплексних чисел може спростити вирішення деяких завдань, оскільки при перемножуванні комплексних чисел їх модулі перемножуються, а аргументи додаються.
Наприклад
![]()
або
![]() .
.
Приклад 1.33.
Знайти який-небудь дійсний
розвязок рівняння
![]() .
.
Розв’язання. З
формули Ейлера виходить, що дане рівняння
можна записати у вигляді
![]() або
або![]() ,
де
,
де
![]() .
Звідки знаходимо
.
Звідки знаходимо![]() |находимо|,
тобто|цебто|
|находимо|,
тобто|цебто|
![]() або остаточно
або остаточно
![]() .
.
МНОГОЧЛЕНИ ВІД ОДНІЄЇ ЗМІННОЇ
Розглянемо многочлени від однієї змінної над полем дійсних чисел .
Многочленом
від однієї змінної над полем
називається вираз виду
![]() ,
де
-
довільне ціле невід’ємне число;
,
де
-
довільне ціле невід’ємне число;
![]() -
елементи
;
-
елементи
;
![]() -
деякі символи.
-
деякі символи.
Многочлени від
змінної
позначатимемо малими латинськими
буквами:
![]() ,
,
![]() тощо.
тощо.
Нехай
![]() .
.
Степінь многочленна
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Введемо операції додавання та множення многочленів:
![]() ;
;
![]() ;
;
![]() ,
,
![]() ;
;
![]() при
при
![]() ;
;
![]() при
при
![]() .
.
Легко довести, що
сукупність многочленів відносно так
введених операцій додавання та множення
утворює кільце, яке називається кільцем
многочленів над полем
і позначається
![]() .
.
У кільці виконується алгоритм ділення з остачею, тобто
![]() ;
;
![]() ;
;
![]() ,
,
такі, що справджується
рівність
![]() .
.
Многочлени
![]() та
називаються відповідно часткою
та остачею від ділення многочлена
на
і визначаються однозначно.
та
називаються відповідно часткою
та остачею від ділення многочлена
на
і визначаються однозначно.
Теорема Гауса. Довільний многочлен n-го степення з комплексними коефіцієнтами має рівно n-коренів, якщо кожен кратний корінь рахувати стільки разів, яка його кратність.
Наслідок: Якщо C₁,C₂…Cn – корені ƒ(х), то ƒ(х)= a0(x-C₁)(x-C₂) … (x-Cn)
Теорема Безу. Многочлен ƒ(х) при діленні на (х-с) дає остачу рівну значенню цього многочлена, при х=0, тобто ƒ(с).
Наслідок: Якщо с- корінь многочлена ƒ(х), то остача від діленняя ƒ(х) на (х-с) дорівнює нулю.
Твердження 1 Якщо многочлен з цілим коефіцієнтами, то цілі корені цього многочлена є дільниками його вільного члена.
Твердження 2.
Якщо
![]() є коренем многочлена
є коренем многочлена
![]() ,
то спряжене комплексне число
,
то спряжене комплексне число
![]() також є коренем цього многочлена.
також є коренем цього многочлена.
Приклад 1.34. Виконати ділення з остачею, якщо
![]() ;
;
![]() .
.
Розв’язання.
![]()

![]()
![]()



![]()
![]()


![]()
![]()


![]()
![]()
Отже,
![]() .
.
![]() є коренем многочлена
тоді і тільки тоді, коли
ділиться на
є коренем многочлена
тоді і тільки тоді, коли
ділиться на
![]() ,
але не ділиться
,
але не ділиться
![]() .
.
Приклад 1.35.
Число
![]() є коренем многочлена
є коренем многочлена
![]() .
Знайти всі інші корені цього многочлена
та розкласти його на множники.
.
Знайти всі інші корені цього многочлена
та розкласти його на множники.
Розв’язання.
Оскільки
-
корінь многочлена
,
то
![]() -
також корінь цього многчлена. За теоремою
Безу многчлен
ділиться на дійсний двочлен
-
також корінь цього многчлена. За теоремою
Безу многчлен
ділиться на дійсний двочлен
![]() .
.
Справді,
![]()
![]()
![]()



![]()
![]()

![]()
![]()
![]()

![]()

![]()
![]()

![]()
Отже,
![]() .
.
Будемо тепер шукати
корені многочлена
![]() серед дільників його вільного члена:
серед дільників його вільного члена:
![]() .
Для знаходження коренів многочлена та
визначення їх кратності можна скористатися
схемою Горнера, або зробити просту
перевірку.
.
Для знаходження коренів многочлена та
визначення їх кратності можна скористатися
схемою Горнера, або зробити просту
перевірку.
Легко перевірити,
що 1 - двократний корінь многочлена
,
тому
![]() .
.
Корені многочлена
![]() легко знайти – це 2 і 3. таким чином, маємо
канонічний розклад многочлена
легко знайти – це 2 і 3. таким чином, маємо
канонічний розклад многочлена
![]() .
.
Спільний дільник
многочленів
і
,
який ділиться на інший спільний дільник
цих многочленів, називається найбільшим
спільним дільником многочленів
,і
і позначається
![]() .
.
Многочлени
,![]() називається взаємно простими, якщо
кожний їх спільний дільник є многочленом
нульового степеня.
називається взаємно простими, якщо
кожний їх спільний дільник є многочленом
нульового степеня.
Для знаходження найбільшого спільного дільника двох многочленів застосовується алгоритм Евкліда.
Приклад 1.36.
Знайти найбільший спільний
дільник многочленів
![]() та
та
![]() .
.
Розв’язання. Ділимо на . При цьому, щоб уникнути дробових коефіцієнтів, перший з них множимо на 3. зрозуміло, що при цьому частка й остача також будуть помножені на 3, що не має істотного значення, бо всі многочлени визначаються з точністю до сталого множника. Маємо
![]()
![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
Оскільки в процесі ділення ще раз було виконано множення на 3, то при цьому частка вийшла неправильна, бо її перший коефіцієнт у 3 рази, а другий – у 9 разів більший за той, який має бути. Що ж до остачі, то вона збільшилась в 9 разів. Оскільки нас цікавить не частка, а остача і оскільки цю остачу можна визначити з точністю до сталого множника, то такий процес ”порушеного ділення” приведе до мети.
Таким чином,
![]() .
Ділимо далі:
.
Ділимо далі:
![]()

![]()
![]()
![]()

![]()
![]()

![]()

![]()
![]()
Отже,
![]() .
Продовжується ділення
.
Продовжується ділення
![]()
![]()

![]()

Таким
чином,
![]() .
.
Завдання 1. З’ясуйте, чи утворюють групу такі множини відносно зазначених операцій:
множина всіх невід’ємних цілих чисел відносно додавання;
множина цілих чисел відносно віднімання;
множина всіх цілих чисел, кратних деякому цілому числу n відносно додавання;
множина раціональних чисел відносно додавання, множення;
множина відмінних від нуля раціональних чисел відносно множення;
множина чисел виду
 ,
де a, b
довільні раціональні числа відносно
додавання;
,
де a, b
довільні раціональні числа відносно
додавання;множина чисел виду , де a, b довільні раціональні числа, не рівні одночасно нулю, відносно множення;
множина степенів
 даного дійсного числа а, де
даного дійсного числа а, де
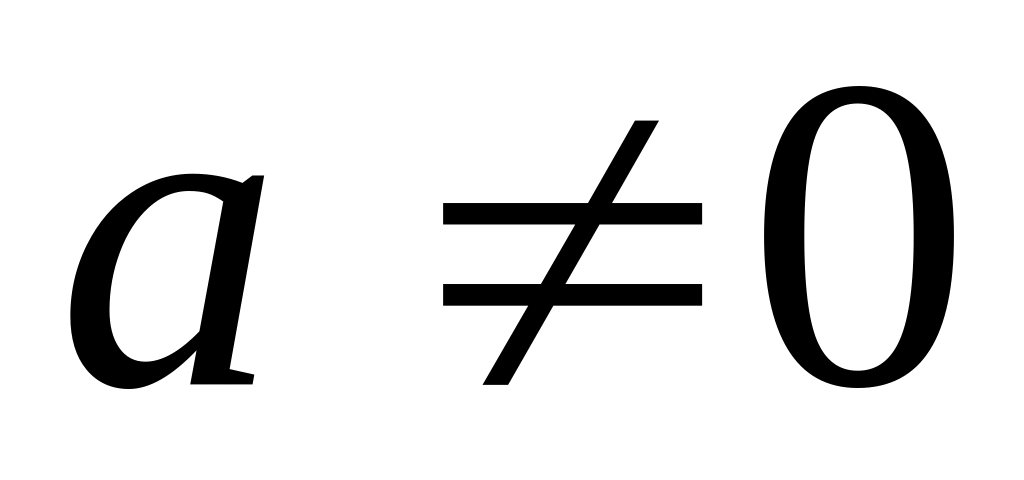 і
і
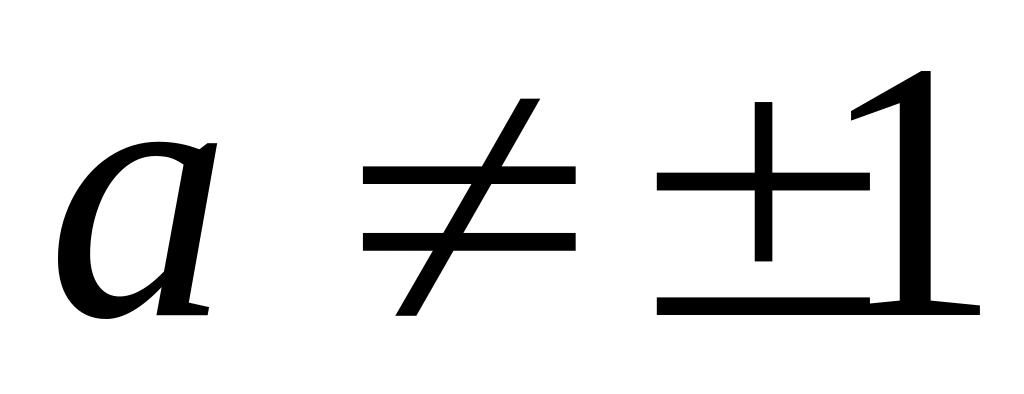 з
цілими показниками t
відносно множення;
з
цілими показниками t
відносно множення;множина всіх підмножин даної множини відносно об’єднання.
м
*
-1
1
-1
1
-1
1
-1
1
мал.2.3.
ножина підстановок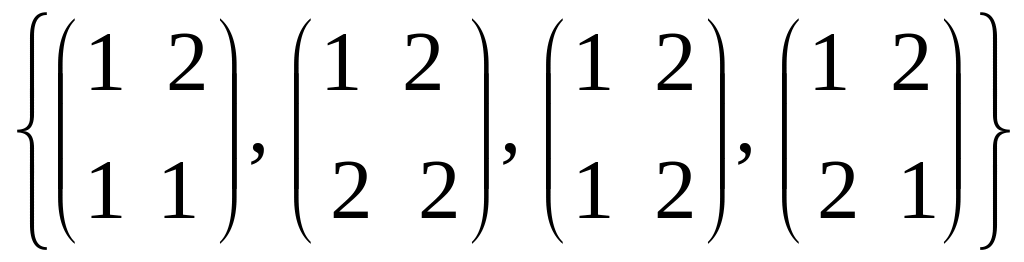 відносно операції множення підстановок
відносно операції множення підстановокмножині М={-1, 1} задана таблицею Келі (мал.2.3.)
м
*
1
і
-1
-і
1
1
і
-1
-і
і
і
-1
-і
1
-1
-1
-і
1
і
-і
-і
1
і
-1
мал.2.4.
ножина М={-1, 1} відносно операції заданої таблицею Келі (мал.2.3.);множина А={1, і, -1, -і} відносно операції заданої таблицею Келі (мал.2.4.);
множина функцій f0(x)=x, f1(x)=1/x, f2(x)=1-x, f3(x)=x/(x-1), f4(x)=(x-1)/x, f3(x)=1/(1-x) відносно суперпозиції функцій;
множина парних підстановок n-го степеня відносно множення підстановок;
множина непарних підстановок n-го степеня відносно множення підстановок;
множина підстановок
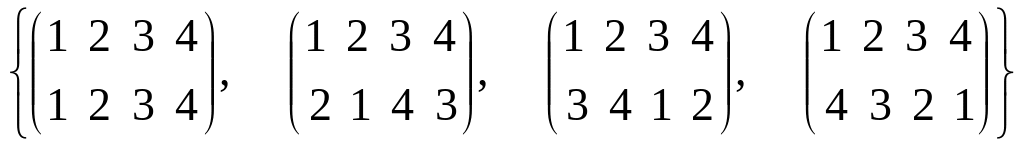 відносно множення підстановок.
відносно множення підстановок.множина всіх чисел виду
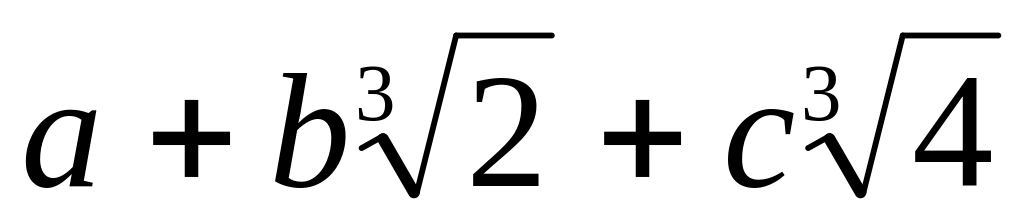 ,
де a, b,
с - довільні цілі числа;
,
де a, b,
с - довільні цілі числа;множина всіх чисел виду , де a, b, с - довільні раціональні числа;
множина всіх чисел виду , де a, b, с - довільні дійсні числа.
множина раціональних чисел, які можна подати у вигляді дробів з парними знаменниками;
множина раціональних чисел, які можна подати у вигляді дробів з непарними знаменниками;
множина чисел виду lg a, де а – довільне дійсне додатне число;
множина многочленів другого степеня
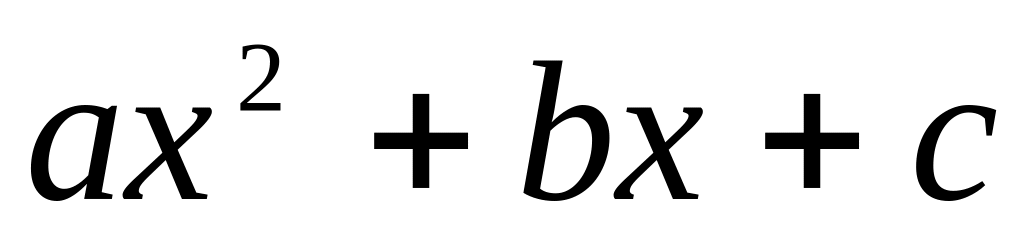 ,
де a, b,
c – раціональні
числа.
,
де a, b,
c – раціональні
числа.
множина многочленів другого степеня , де a, b, c –дійсні числа.
Завдання 2. Знайти геометричне місце точок, що зображають комплексні числа , які задовольняють такі умови:
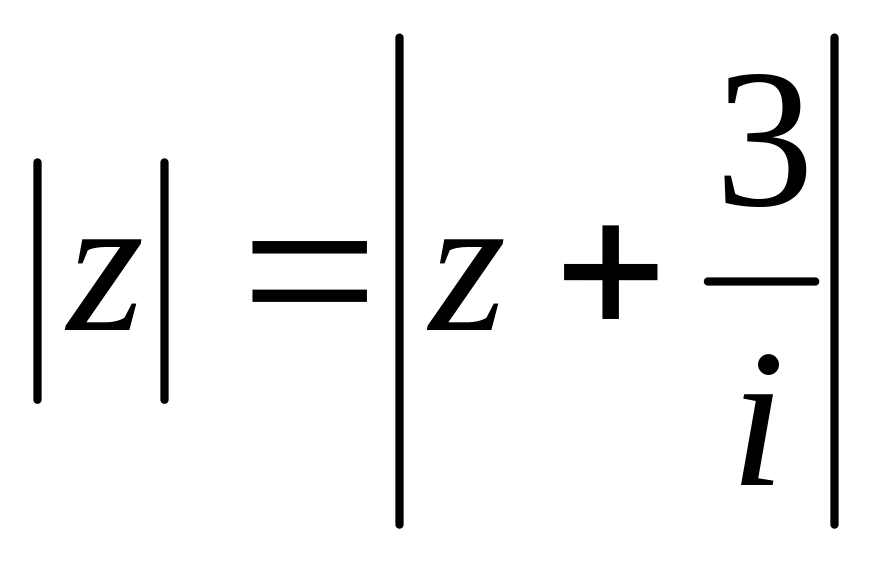 ;
;
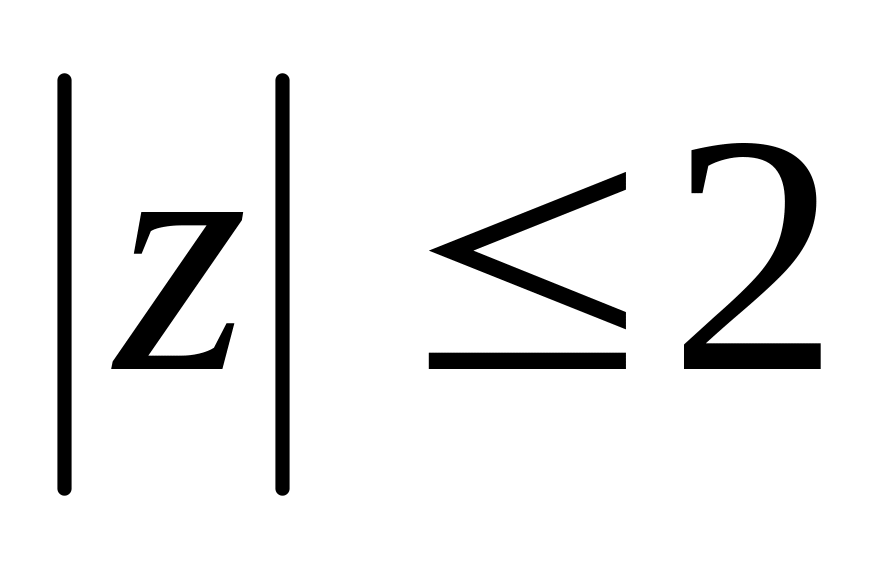 .
.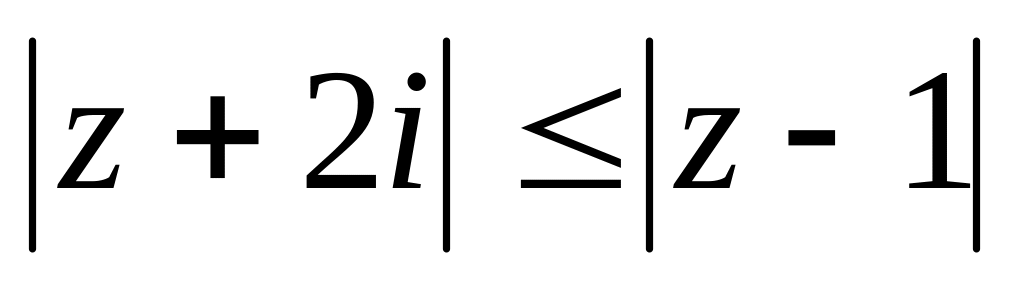 .
.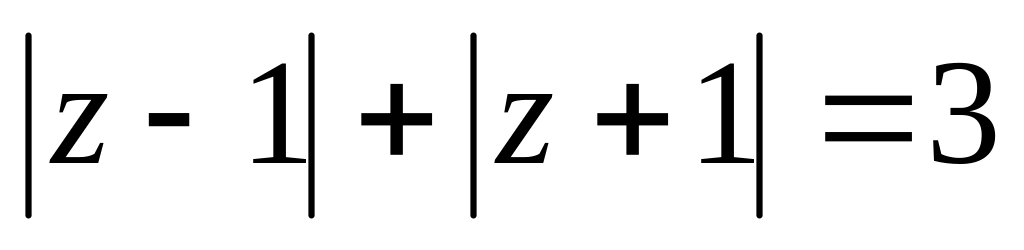 .
.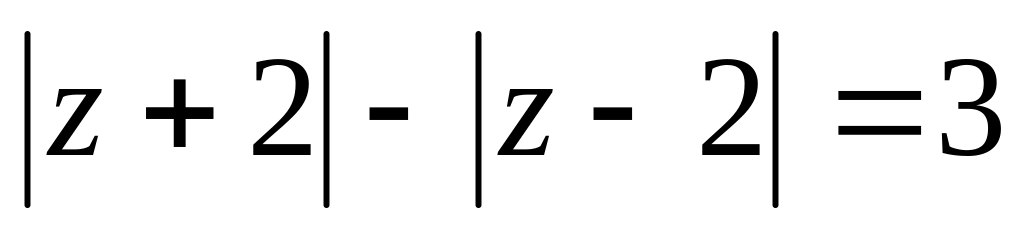 .
.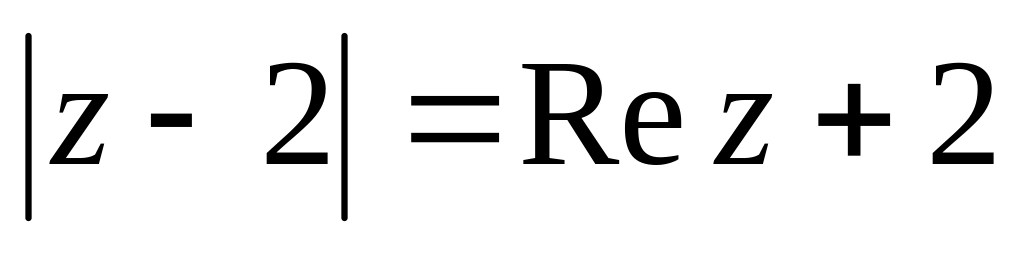 .
.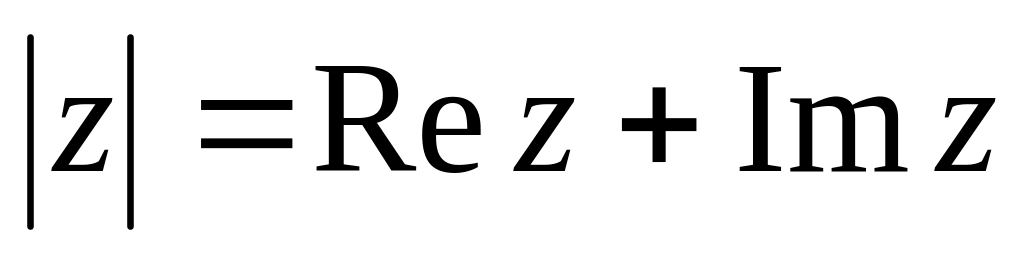 .
.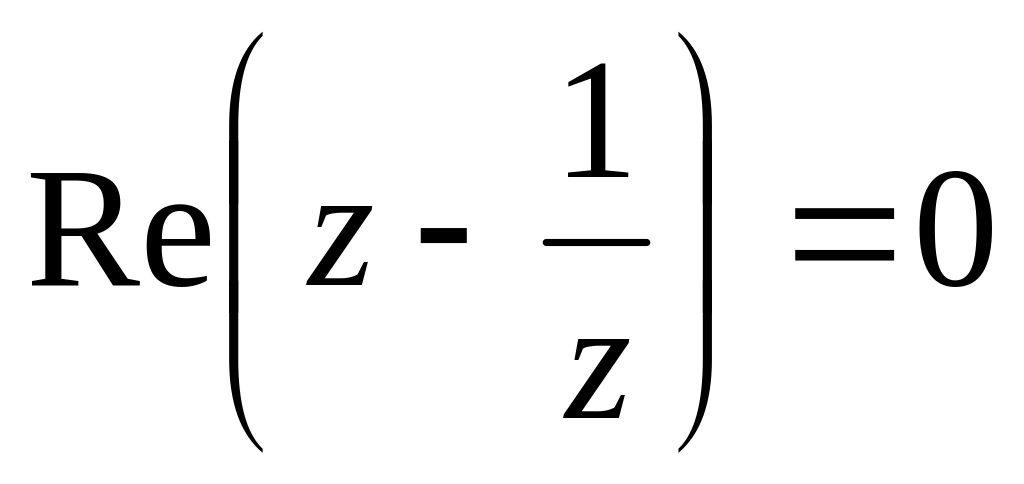 .
.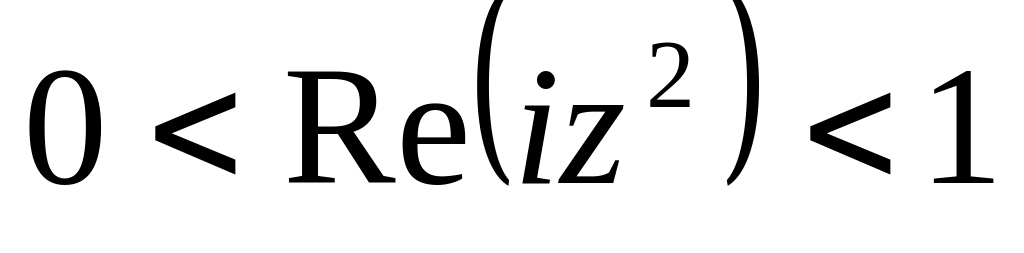 .
.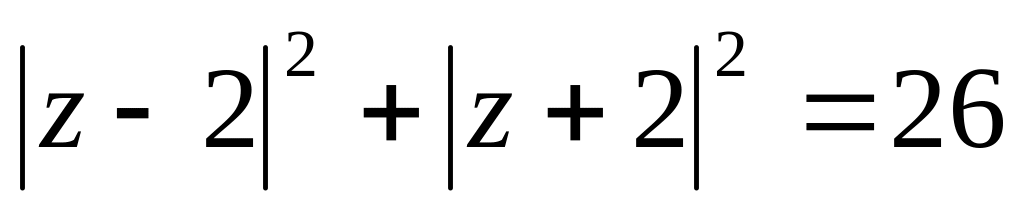 .
.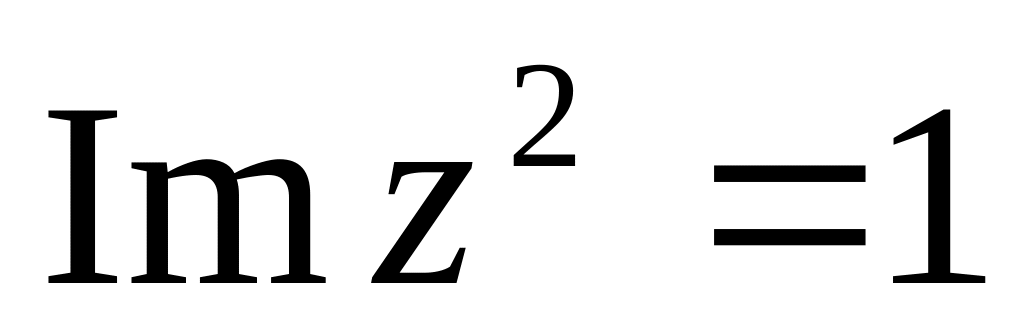 .
.|z — z 1|<4, де z 1 = 3 — 5i.
|z + z 2|>6, де z 2 = 1—i.
1 < |z — i|< 3.
0< |z +i|< 1.
0<Re(3iz)<2.
Re(l/z)>a, де а = const, a R
Re ((z — ai)/(z + ai)) = 0, де a = const, a R.
Im(iz)<2.
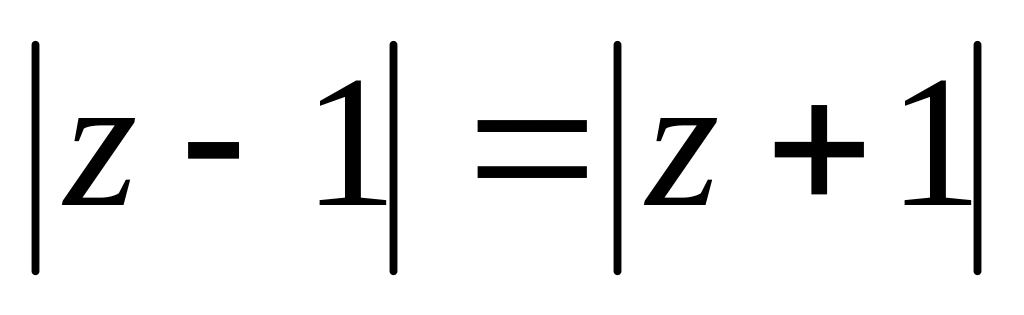
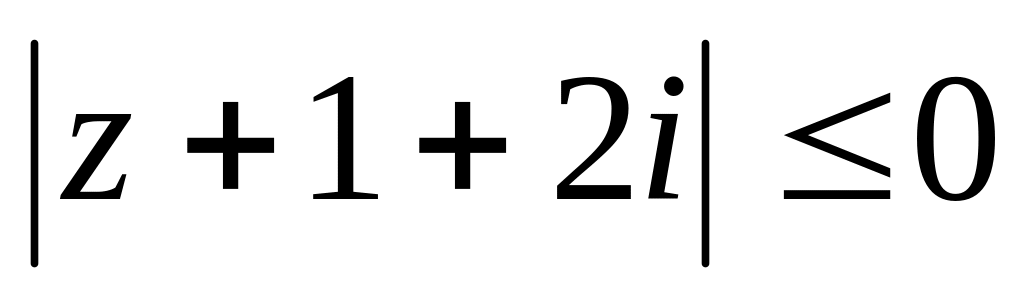
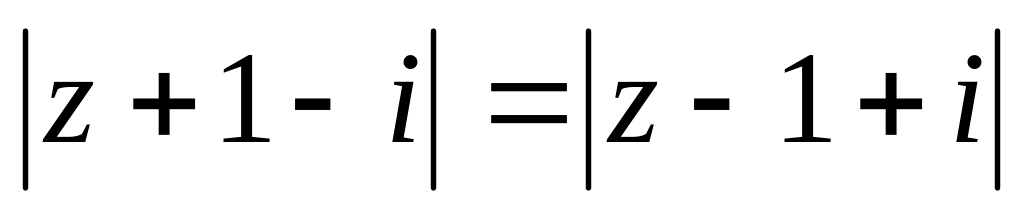
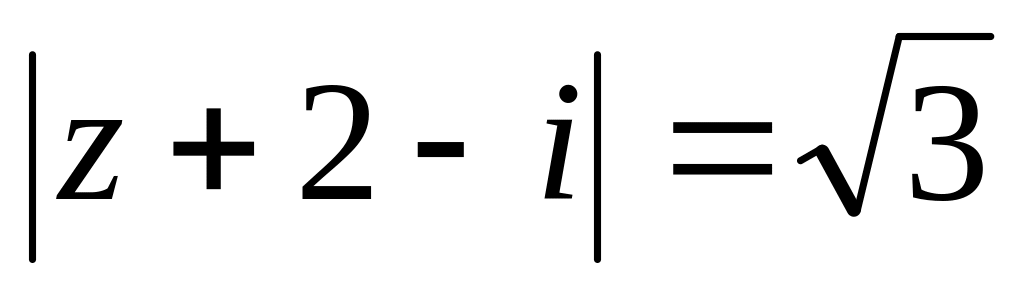
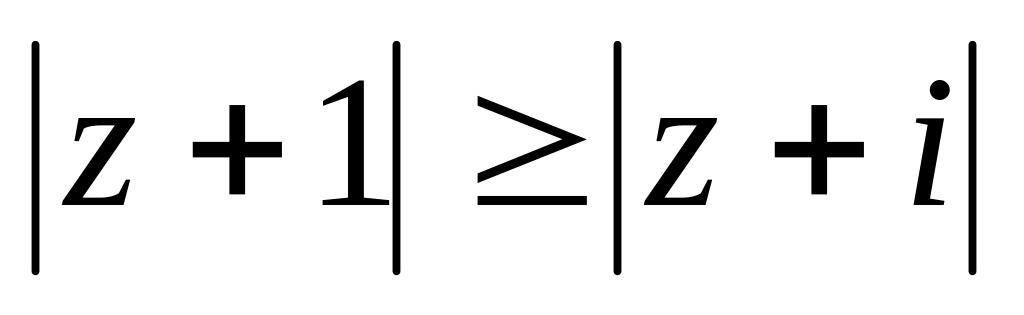
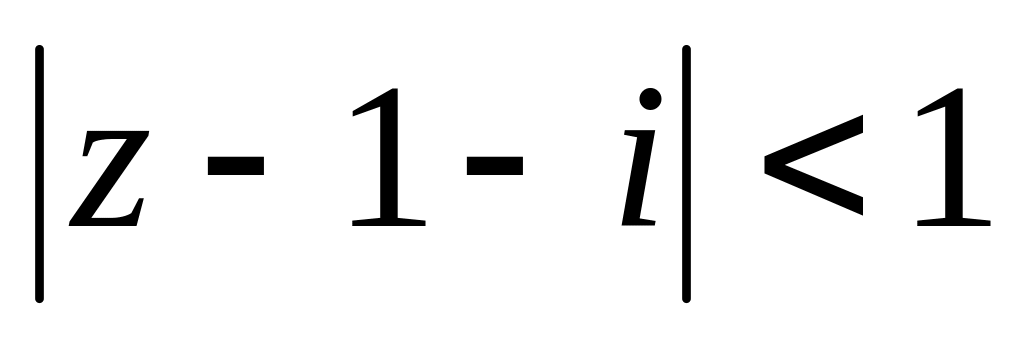
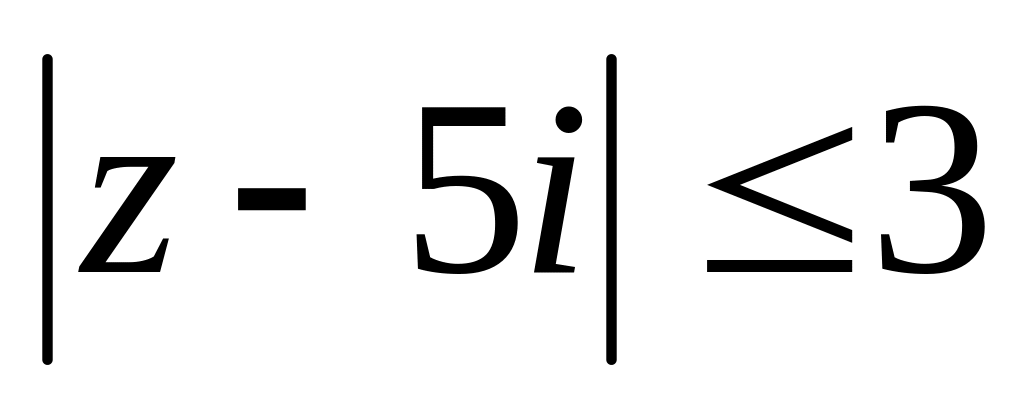
Завдання 3. Обчислити.
а/
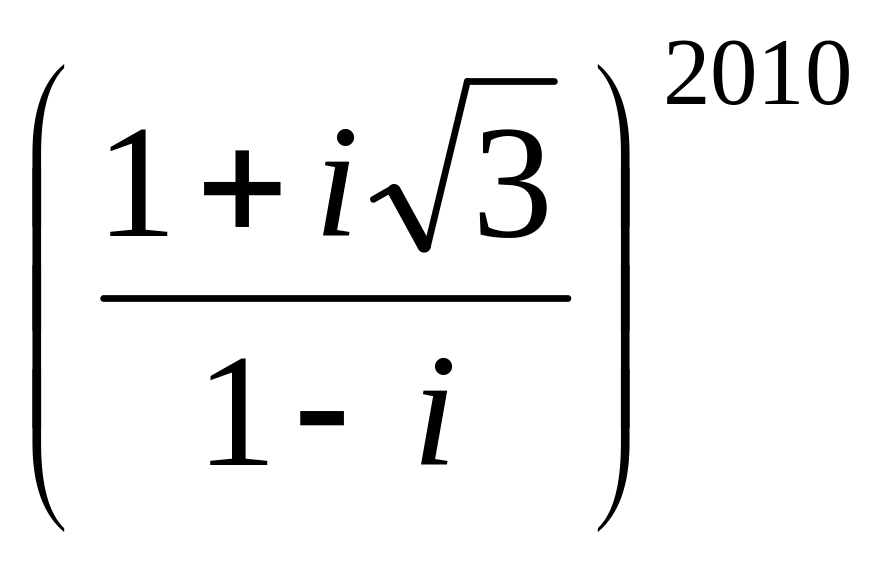 ;
б/
;
б/
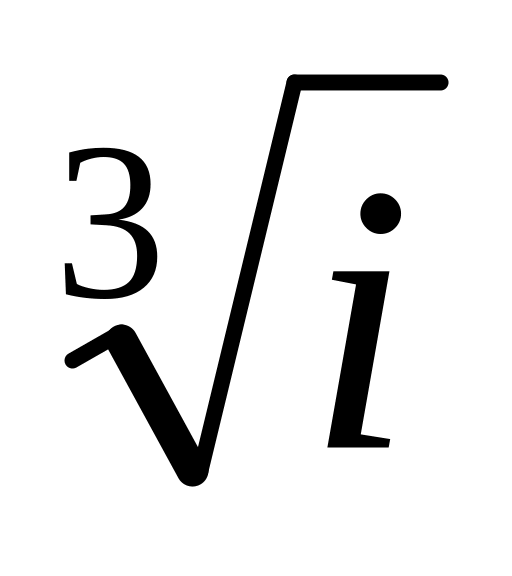 .
.а/
 ;
б/
;
б/
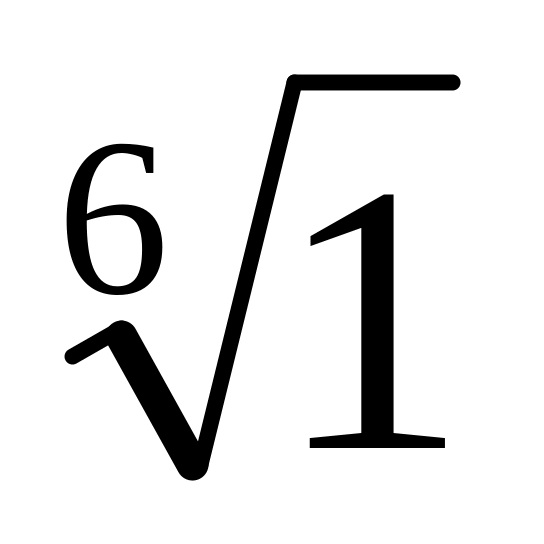 .
.а/
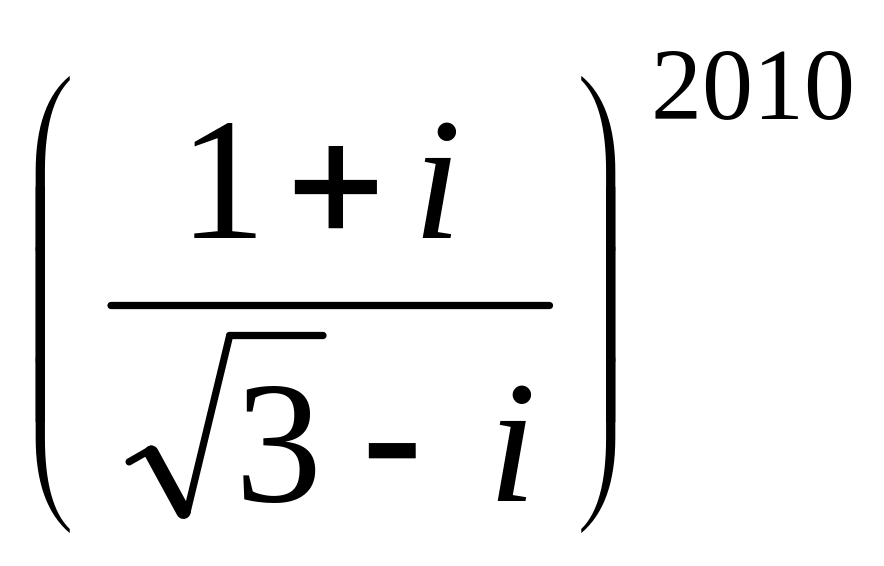 ;
б/
;
б/
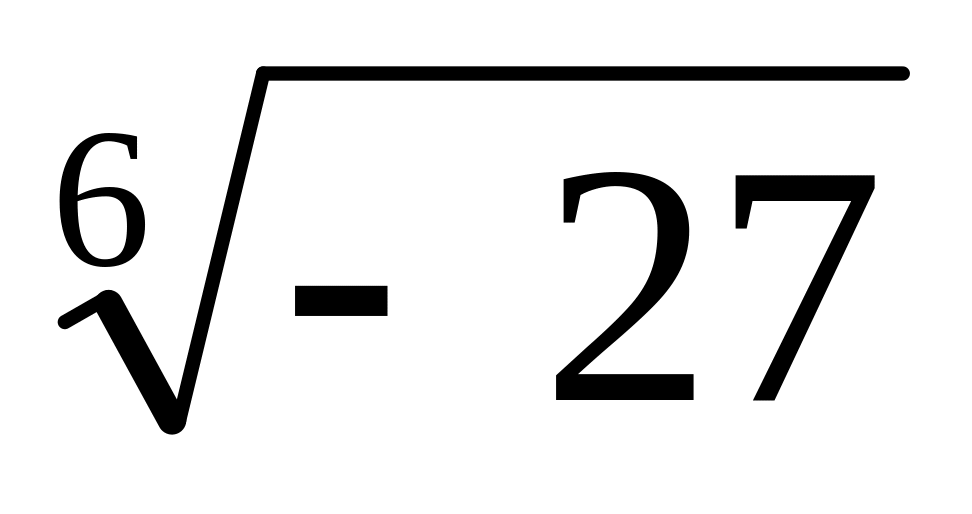 .
.а/
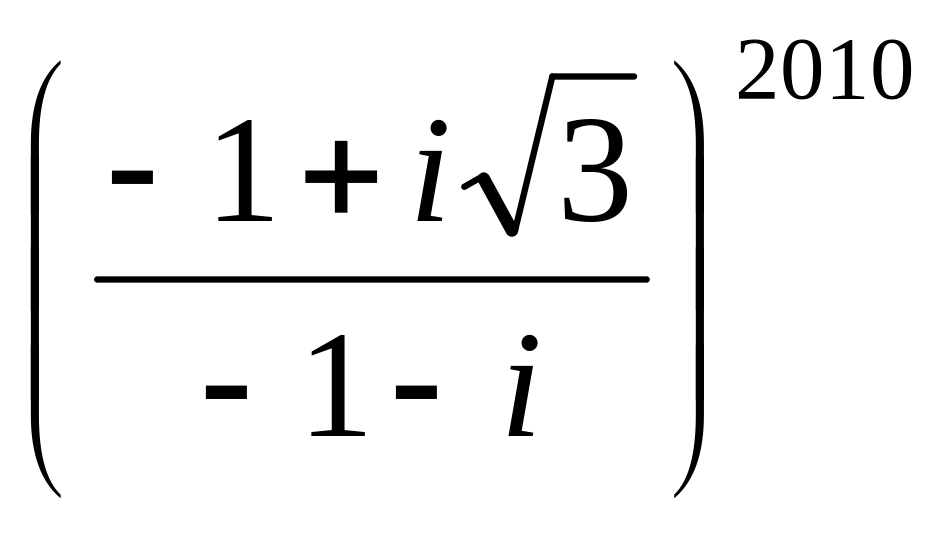 ;
б/
;
б/
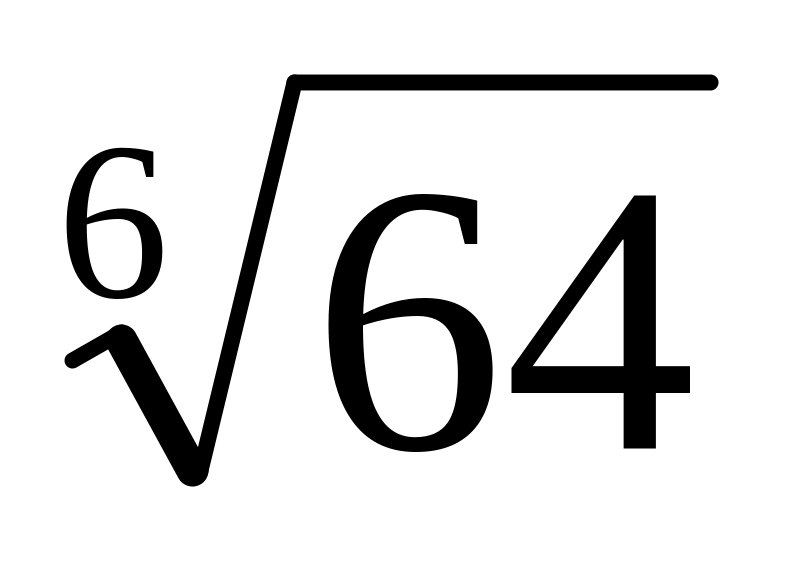 .
.а/
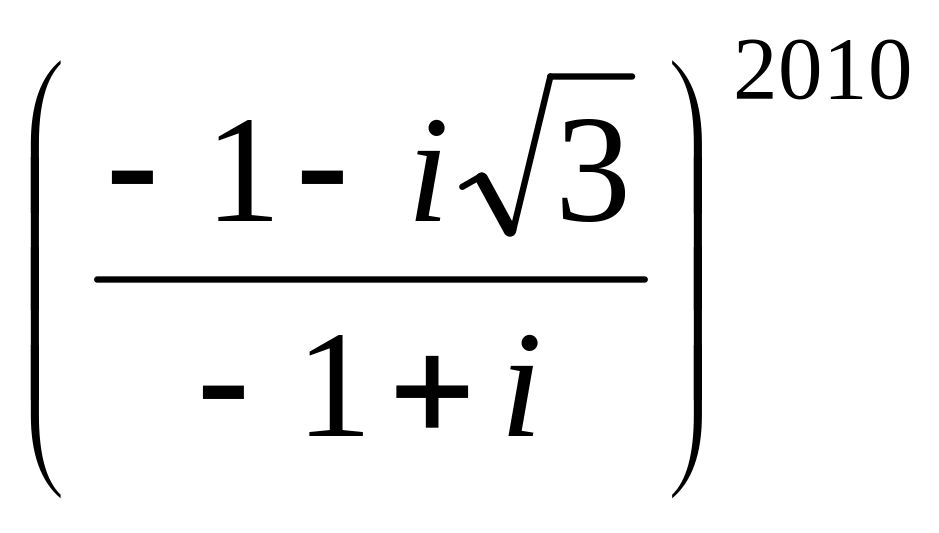 ;
б/
.
;
б/
.а/
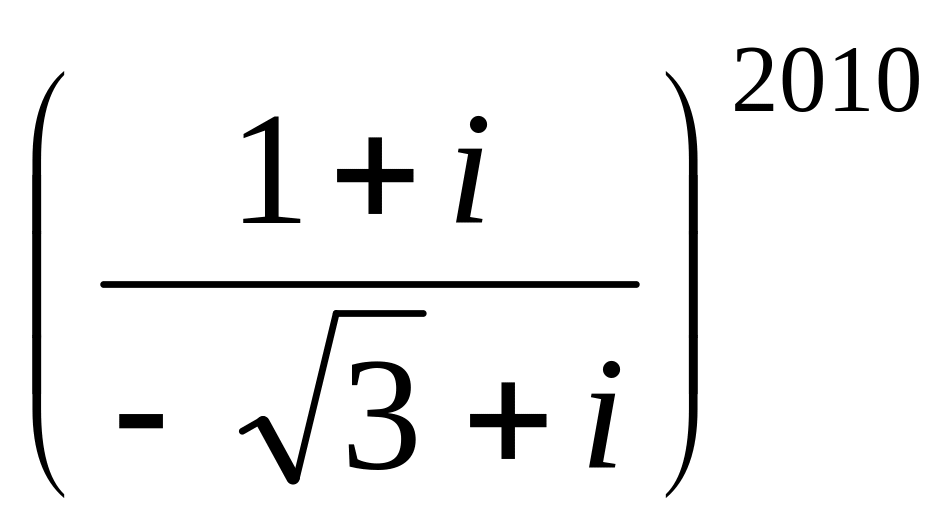 ;
б/
;
б/
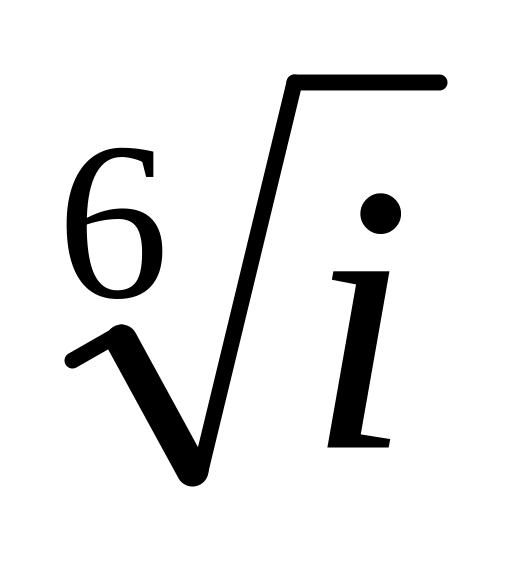 .
.а/
 ;
б/
;
б/
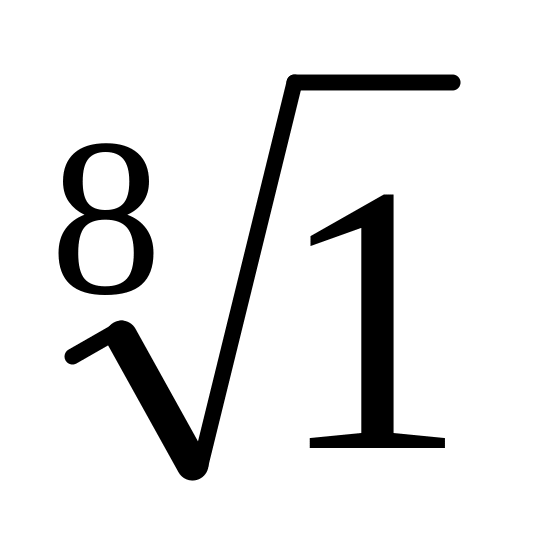 .
.а/
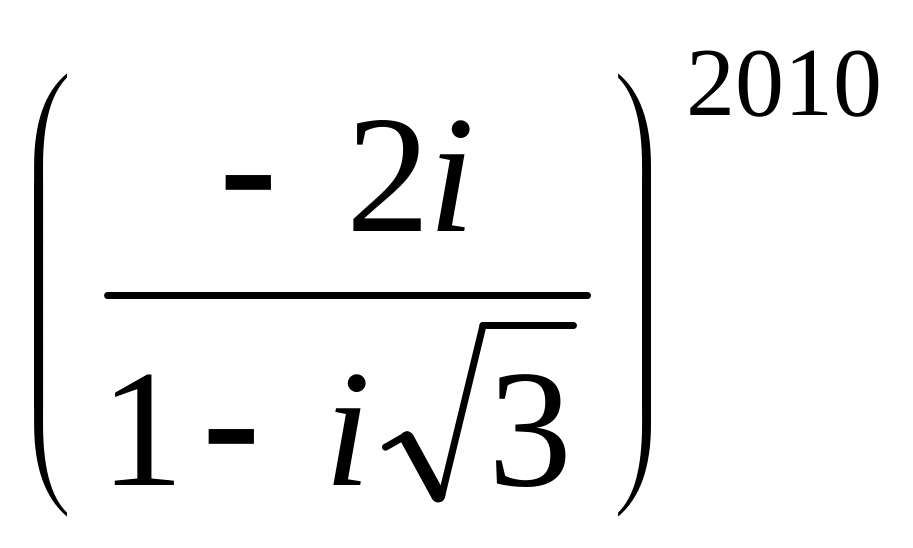 ;
б/
;
б/
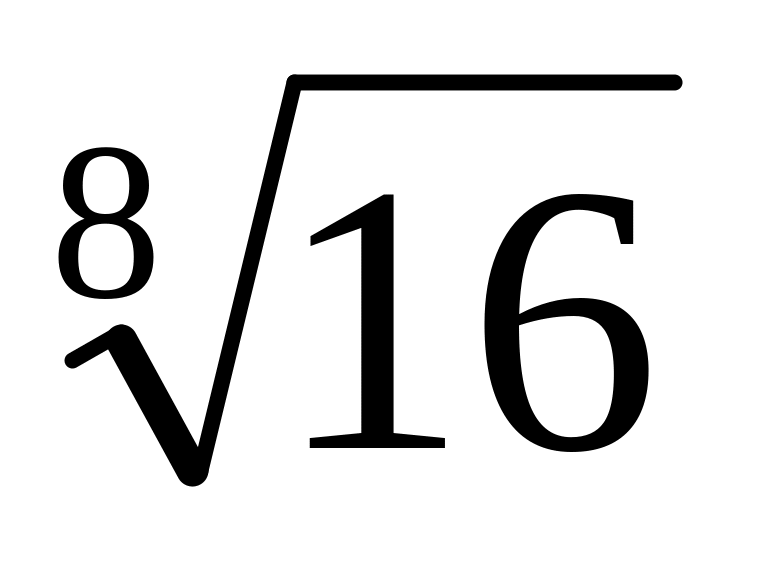 .
.а/
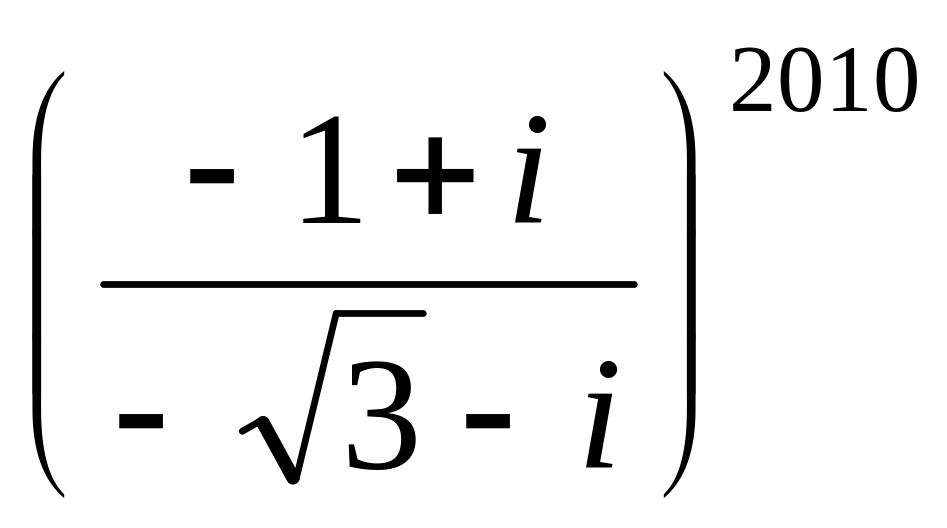 ;
б/
;
б/
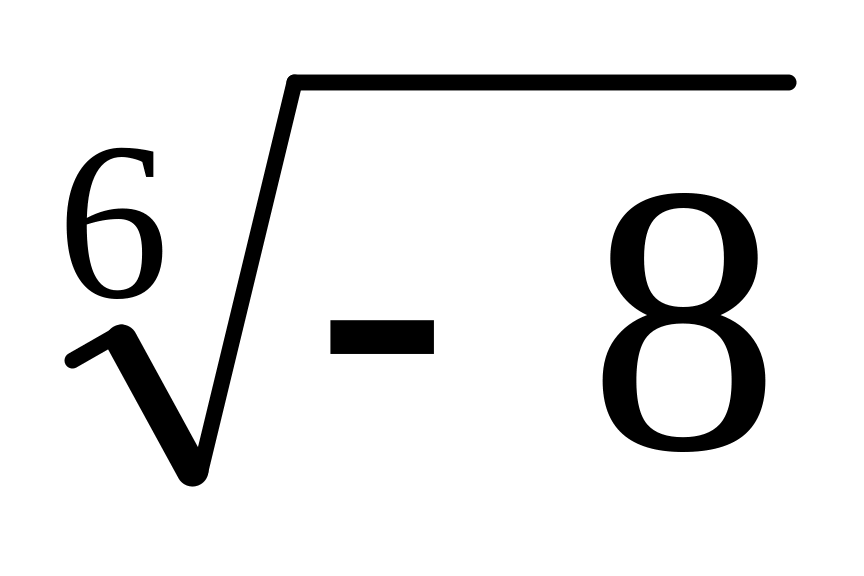 .
.а/
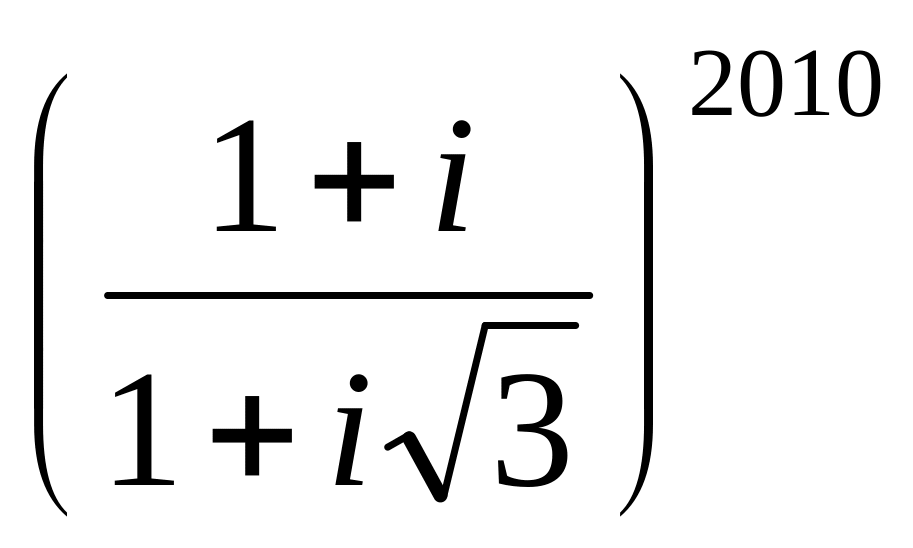 ;
б/
.
;
б/
.а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
а/ ; б/ .
Завдання 4. Для варіантів 1 – 12 користуючись алгоритмом Евкліда, знайти найбільший спільний дільник многочленів, для варіантів 13-25 знайти всі інші його корені та розкласти многочлен на незвідні дійові множники, якщо відомо, що число - корінь многочлена .
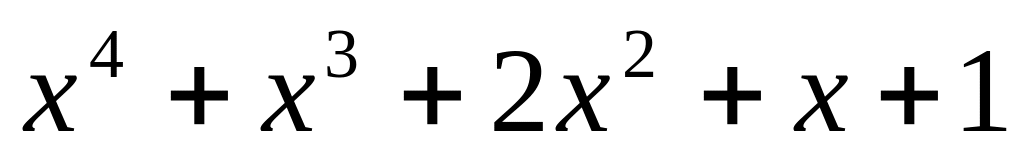 ;
;
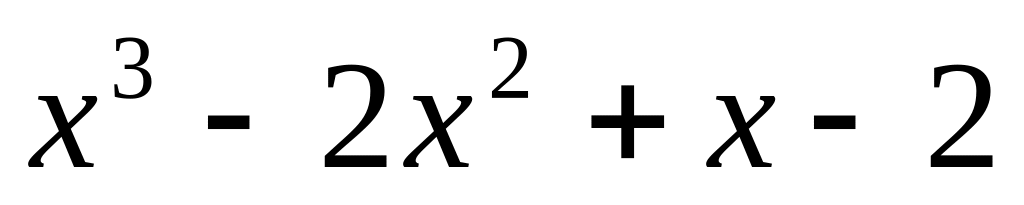 .
.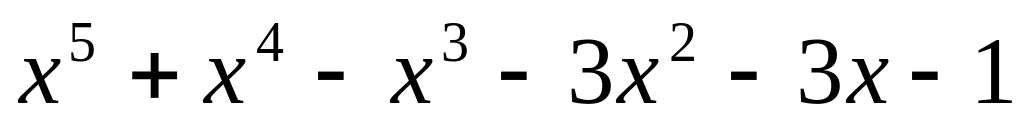 ;
;
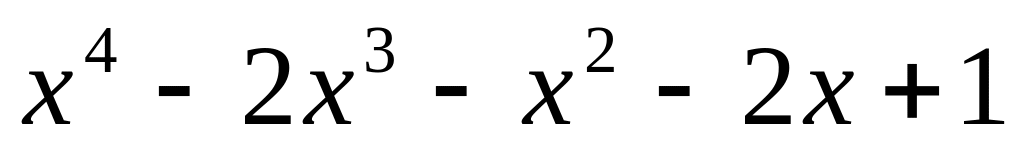 .
.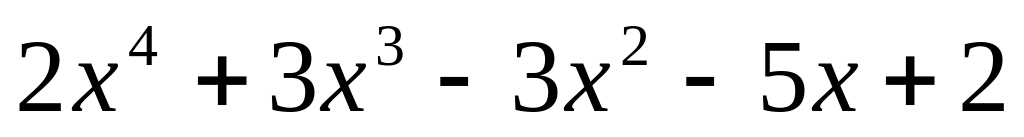 ;
;
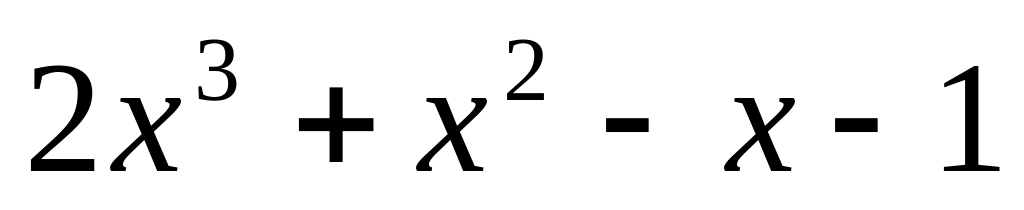 .
.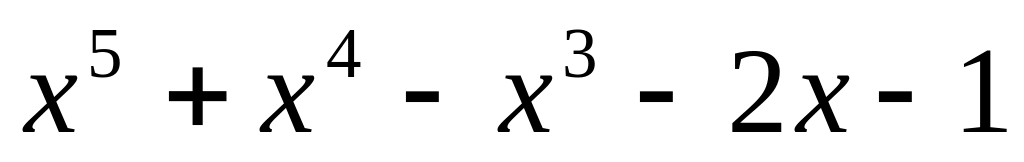 ;
.
;
.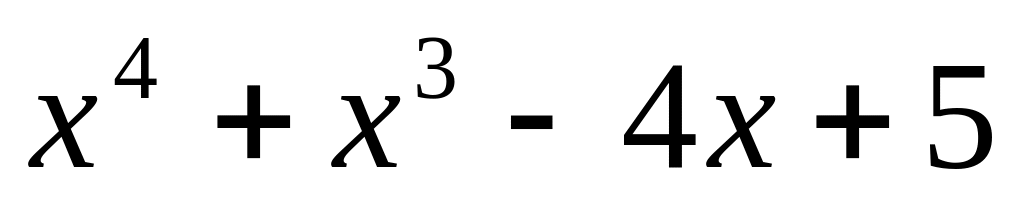 ;
;
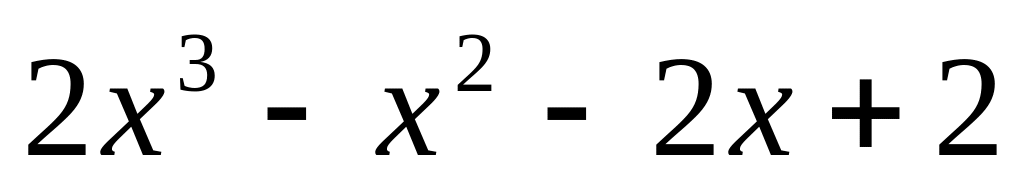 .
.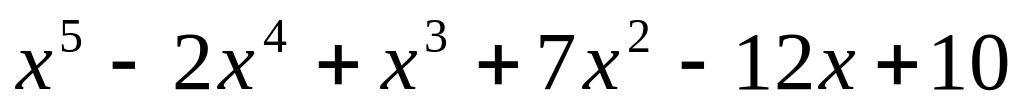 ;
;
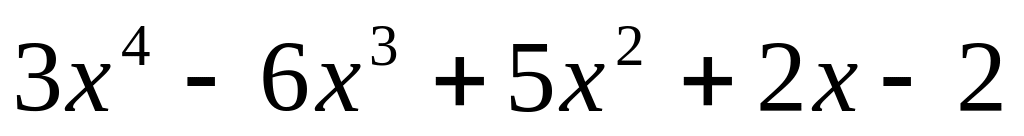 .
.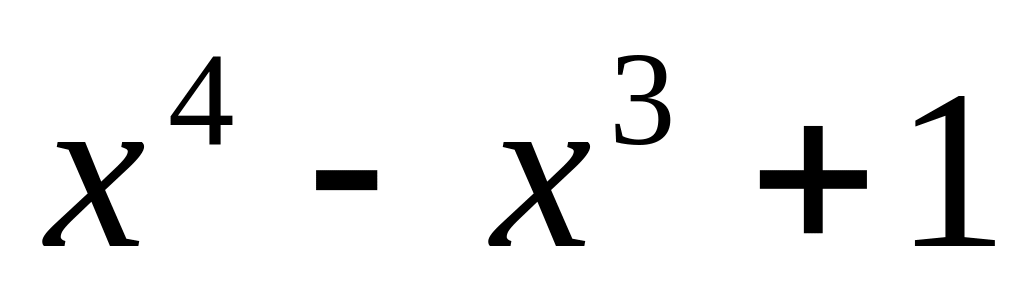 ;
;
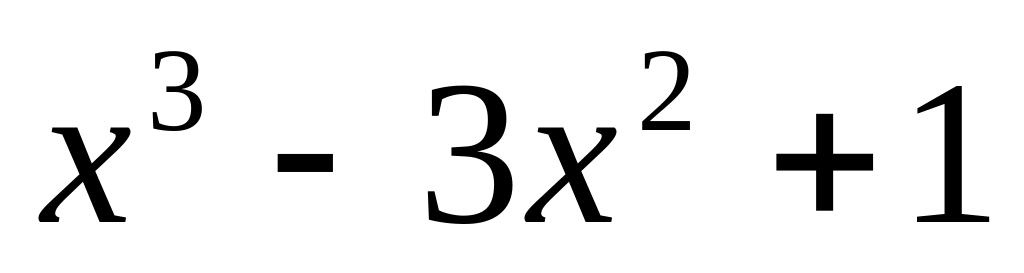 ;
;
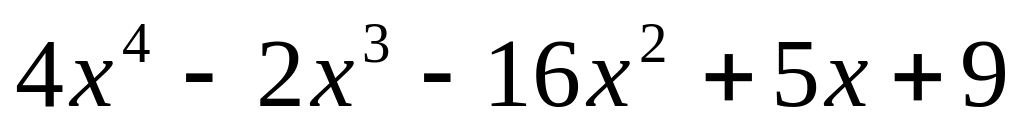 ;
;
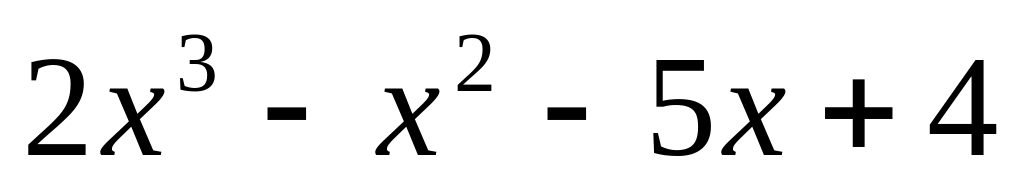 .
.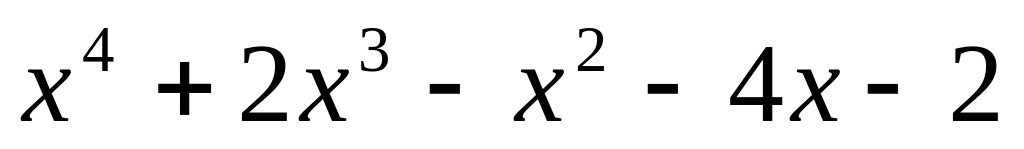 ;
;
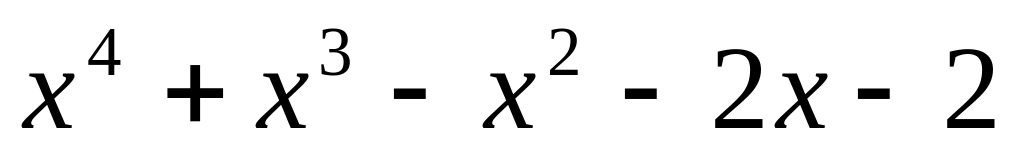 .
.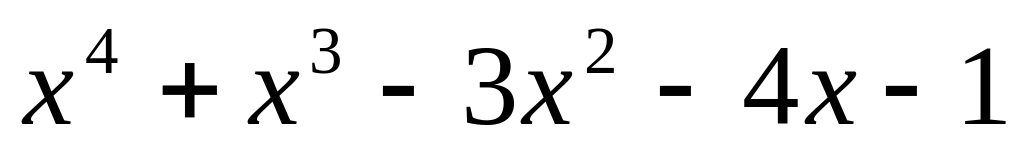 ;
;
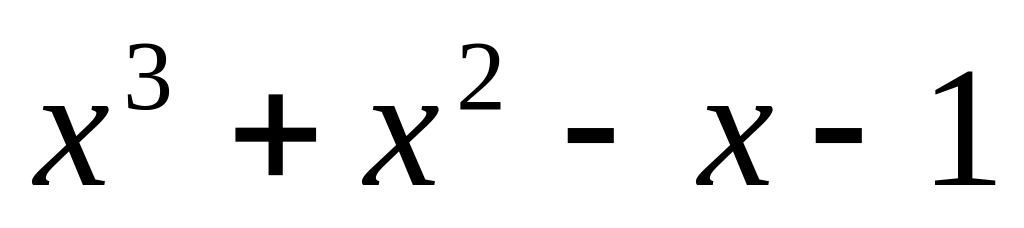 .
.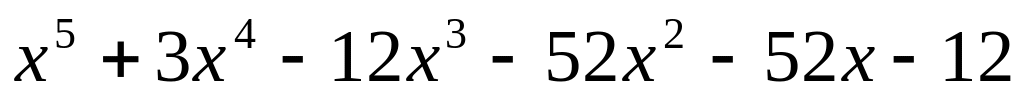 ;
;
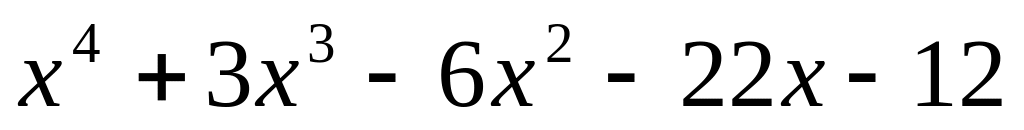 .
.;
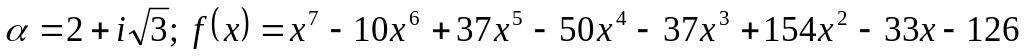
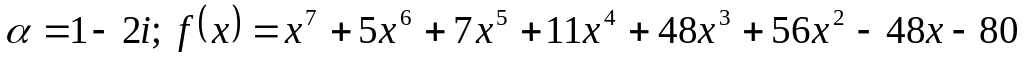 .
.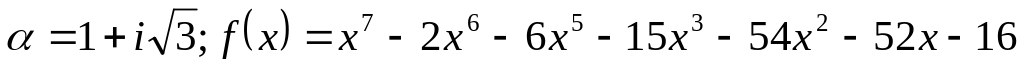 .
.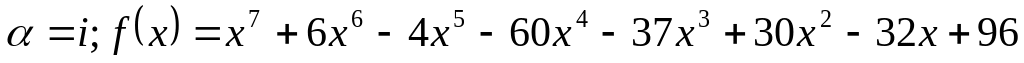 .
. .
.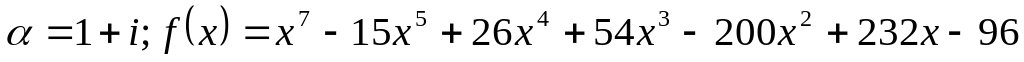 .
. .
.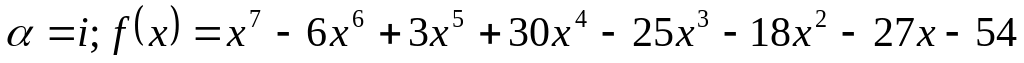 .
.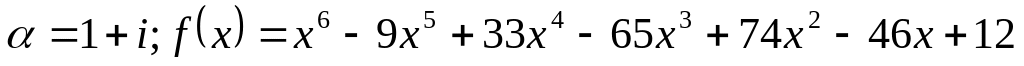 .
.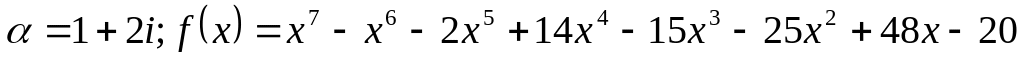 .
..
.
.
