
Кільце.
Множина К, на якій визначено дві алгебраїчні операції „+”(додавання) і „”(множення) називається кільцем, якщо виконуються наступні умови (аксіоми кільця):
Множина К є комутативною групою відносно операції „+”.
2. Операція „” асоціативна .
3. Операції „+” і
„” зв’язані
законами дистрибутивності: для будь-яких
елементів а, b і с з К виконується
рівність
![]() і
і
![]() .
.
Формальний запис аксіом кільця такий:
На множині К задано дві алгебраїчні операції „+” і „”.
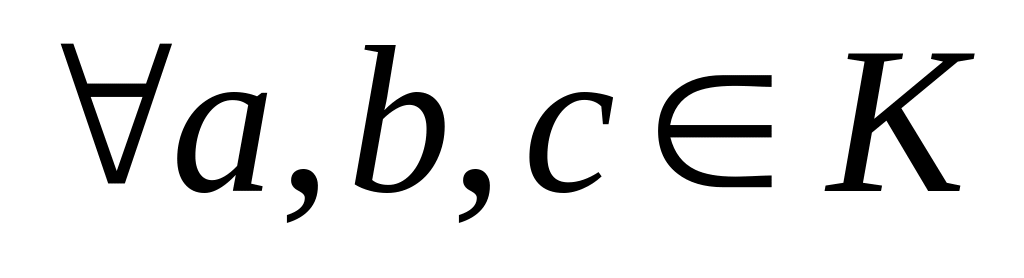 : (a+b)+c=a+(b+c).
: (a+b)+c=a+(b+c).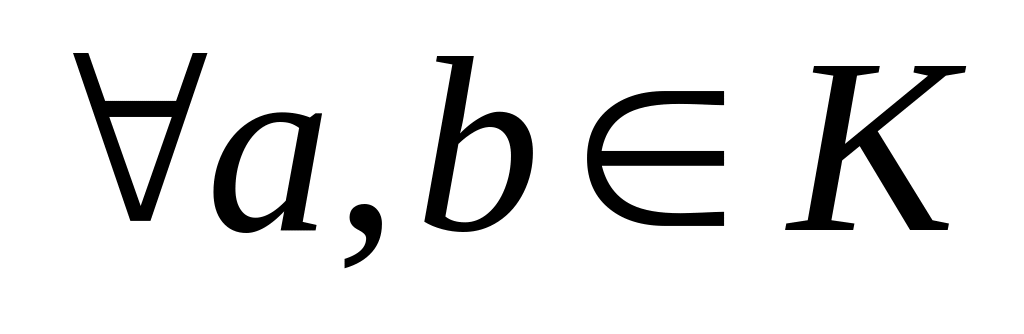 : a+b=b+а.
: a+b=b+а.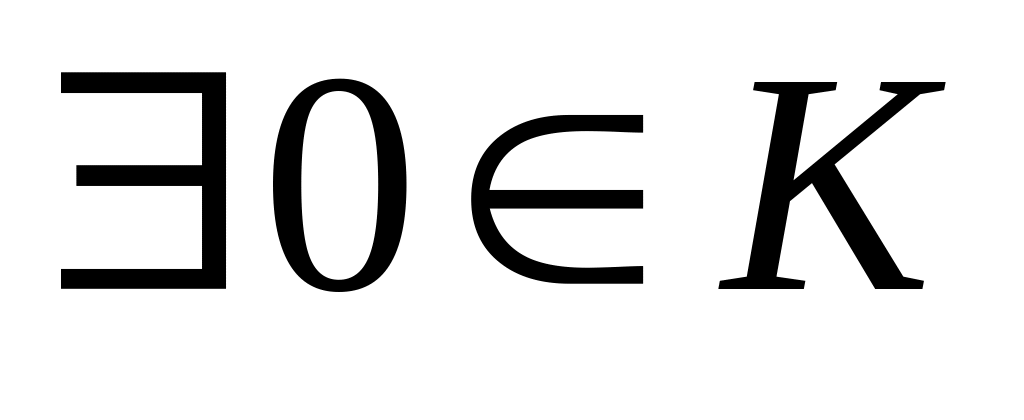 ,
,
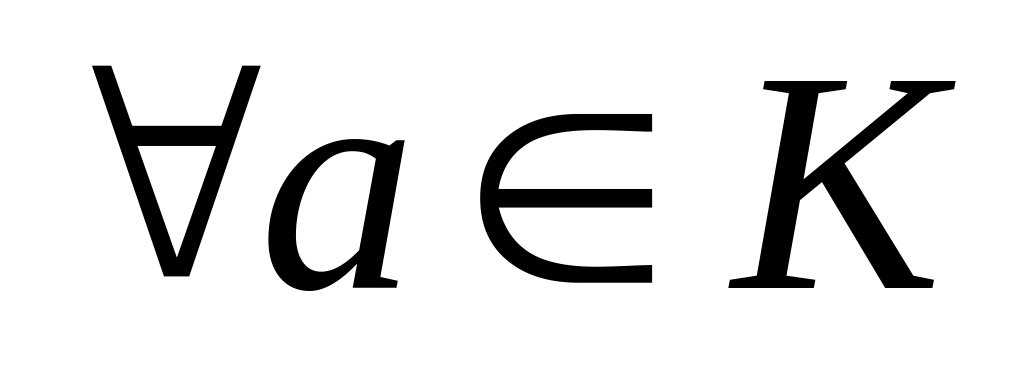 :
a+0=a.
:
a+0=a.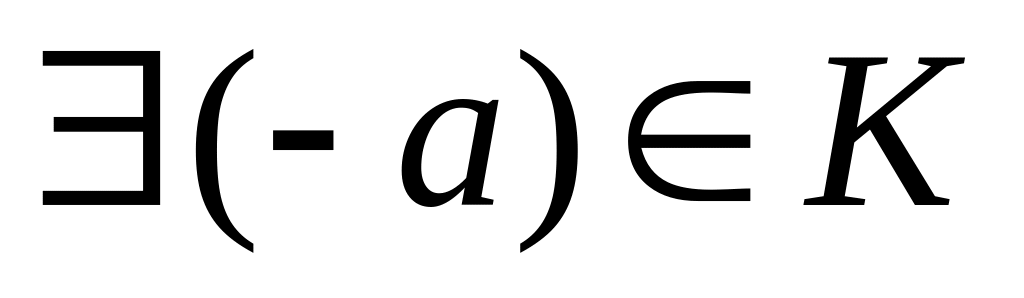 :
a+(-а)=0.
:
a+(-а)=0.: (ab)c=a(bc).
: (a+b)c=ac+bc.
: a(b+c)=ab+ac.
Приклад 1.26. Множина парних цілих чисел є кільцем. Справді, сумою і добутком двох парних цілих чисел є відповідне парне число. Додавання цілих чисел є комутативним, то і для будь-яких парних чисел a і b виконується : a+b=b+а. Число 0 належить до множини парних цілих чисел, тобто виконується четверта умова – існує нейтральний елемент відносно додавання. Для кожного парного цілого числа а існує протилежне йому парне ціле число (-а). Додавання і множення цілих чисел задовольняють умови асоціативності і дистрибутивності, тобто умови 6 – 8.
Якщо операція множення у кільці є комутативною, то кільце називають комутативним.
Звертаємо увагу на те, що в кільці завжди існує нейтральний елемент відносно додавання 0 (нуль), а нейтрального елемента відносно множення може і не бути. Кільце в якому існує нейтральний елемент відносно множення 1 (одиниця) називається кільцем з одиницею.
Оскільки кільце
є абелевою групою відносно додавання,
то мають місце відомі властивості:
єдиність нуля і протилежного елемента,
закон скорочення, єдиність розв’язку
рівняння
![]() рівність
рівність
![]() .
.
Прямими наслідками з аксіом кільця є відомі „правила знаків” та правило множення на нуль .
Теорема. Для будь-яких елементів a, b кільця:
а) a0 = 0a = 0;
б) a(-b) = - (ab);
в) (-a)(-b) = ab.
Доведення. а) З рівності a0 =(0+0)a = 0а + 0а і 0а = 0а+ 0 випливає, що 0а + 0а = 0а+ 0. Тепер за законом скорочення 0а = 0. Аналогічно одержимо а0 = 0.
б) Твердження a(-b) = -(ab) випливає з низки рівностей: а(-b) = 0+a(-b) = -(ab)+ab+a(-b) = -(ab)+a(b+(-b)) = -(ab)+0 = -(ab).
Твердження в) пропонуємо довести самостійно.
Тіло. Поле.
Елемент а кільця з одиницею називається оборотним, якщо він має обернений відносно операції „”.
Кільце з одиницею в якому кожний ненульовий елемент оборотній називається тілом. Комутативне тіло називається полем.
Іншими словами, поле Р – це множина, на якій задано дві алгебраїчні операції так, що відносно першої операції Р є абелевою групою, а відносно другої операції абелевою групою є множина Р* = Р\{0} (це так звана мультиплікативна група поля).
Приклад 1.27. Показати, що множина раціональних чисел є полем.
Покажемо по кроках, що
1) множина раціональних чисел є комутативним кільцем,
2) множина раціональних чисел містить одиницю відносно операції множення,
3) у множині раціональних чисел кожен елемент має обернений відносно множення, тобто множина раціональних чисел є тілом,
4) у множині раціональних чисел множення комутативне.
Виконання цих чотирьох умов і буде свідченням того, що множина раціональних чисел є полем.
