Основні закони операцій над множинами:

1. Закон тотожності: А = А.

2. Закон протиріччя: .

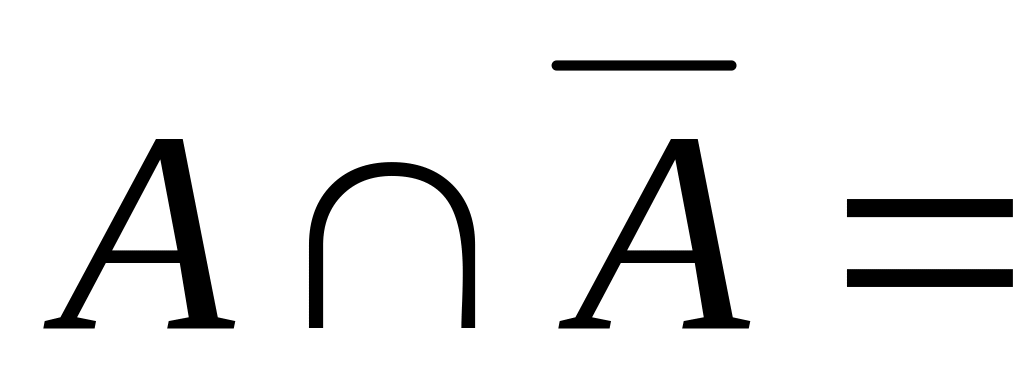3. Закон виключення третього: .

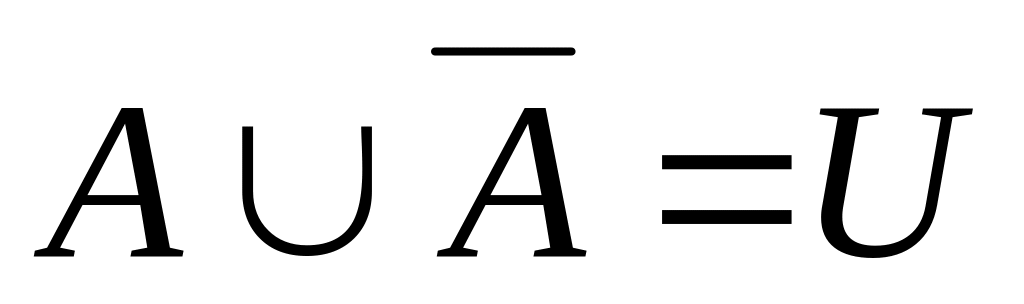4. Закони ідемпотентності: , .

5. Закони комутативності: АВ = ВА і АВ = ВА.

6. Закони асоціативності: А(ВС) = (АВ)С і А(ВС) = (АВ)С.

7. Закони дистрибутивності: (АВ)С = (АС)(ВС) і (АВ)С = (АС)(ВС).

8. Закони поглинання: , .

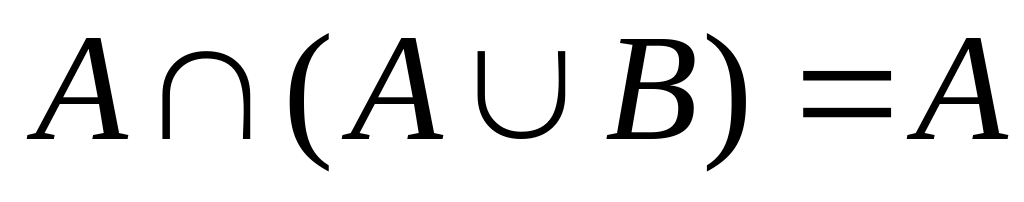9. Закони де Моргана: , .

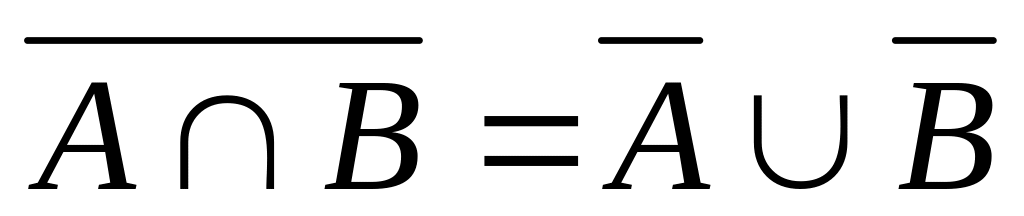10. Закон подвійного заперечення: .

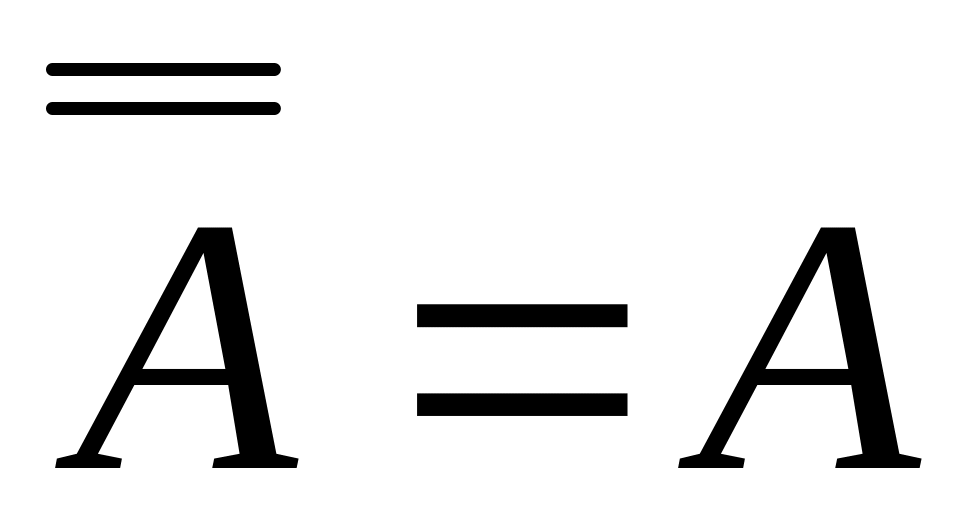Якщо аА і bВ, то пару елементів а і b, записану (а, b), називають впорядкованою парою, при цьому вважають, що пари (а₁, b₁) і (а₂, b₂) рівні, якщо а₁=а₂ і b₁= b₂. Множину, елементами якої є всі впорядковані пари (а, b), де аА і bВ, називають прямим або декартовим добутком множин А і В, який позначають АВ. Зауважимо, що АВВА, коли АВ.

Приклад 1.3. a) Нехай А={1, 2}, a B={2, 3}, то АВ={(1, 2), (1,3), (2, 2), (2, 3)}, a ВА={(2, 1), (2, 2), (3, 1), (3, 2)}.

б) Нехай А=={a, b, c}, a B={a, f}, то АВ ={(a, a), (a, f), (b, a), (b, f), (c, a), (c, f)}, a ВА={(a, a), (a, b), (a, c), (f, a), (f, b), (f, c)}.

Декартів добуток АА часто називають декартовим квадратом множини А. Згідно з означенням декартового добутку АА = {(х; у)| х А, у А}.

Наприклад, декартів квадрат RR=R², множини дійсних чисел - це множина всіляких пар дійсних чисел. Якщо на площині вибрати прямокутну систему координат, то ці пари стають назвами точок площини, і таким чином множина R² дістає важливе геометричне тлумачення. Ототожнивши назви точок (тобто елементи із R²) з самими точками, можна сказати, що R²– це множина точок площини.

Найпростіші властивості декартових добутків:

1. (АВ)С=(АС)(ВС), С(АВ)=(СА)(СВ).

2. (АВ)С=(АС)(ВС), С(АВ)=(СА)(СВ).

3. (А₁А₂)(В₁В₂)=(А₁В₁)  (А₂В₂).

4. (A\B)С=(АС)\(ВС), С(А\В)=(СА)\(СВ).

5. AB=  A=  B=.

Розглянемо доведення однієї з цих властивостей, а саме С(А\В)=(СА)\(СВ). За означенням (x, y)  С(А\В) тоді і тільки тоді, коли x  С і y  А\В, тобто x  С, y  А i y В. Це означає, що (x, y) СА i (x, y)  СВ. Звідси (x, y)  (СА)\(СВ).

Доведення решти властивостей пропонуємо виконати самостійно.

Під відношення між елементами множини розуміють який-небудь зв’язок між цими елементами. Наприклад на множині натуральних чисел вам відомі відношення більше (>) і менше (<), а в геометрії, на множині прямих – відношення паралельності чи перпендикулярності. Задавати відношення можна різними способами. Один з них – за допомогою пар. Наприклад на множині А ={1, 2, 3, 4, 5} задамо відношення “більше” - тобто випишемо всі пари елементів, де перше число більше за друге: (2, 1), (3,1), (3, 2), (4,1), (4,2), (4,3), (5,1), (5, 2), (5,3), (5,4). Така множина пар є підмножиною декартового добутку АА. Бінарним відношенням , заданим у множині A є деяка підмножина  декартового добутку AA. Розглядають також відношення між елементами двох різних множин. Відношенням між елементами множин А і В називається будь-яка підмножина  декартового добутку АВ. Позначають відношення буквою  (від латинського слова relatio – відношення). Для бінарного відношення пишуть ab замість (a, b)  .

Об’єднання і перетин двох відношень між множинами А і В – це, відповідно, об’єднання і перетин відповідних підмножин декартового добутку.

Якщо ₁АВ і ₂ВС – два бінарні відношення, то можна означити добуток відношень _1₂, як наступну підмножину декартового добутку АС:

_1₂={(a, c) АС |  b (a, b)  ₁  (b, c)  ₂}.

Нехай АВ – бінарне відношення. Тоді обернене бінарне відношення ^-1 є наступною підмножиною декартового добутку ВА: ^-1={(b, a)  ВА | (a, b)  }.

Бінарне відношення  на множині АА називається рефлексивним, якщо a : aa. Прикладами рефлексивних відношень є відношення подібності на множині трикутників (будь-який трикутник подібний сам до себе), відношення рівносильності на множині рівнянь і т.д.

Бінарне відношення  на множині АА називається симетричним, якщо a, b : ab  ba. Відношення паралельності на множині прямих, відношення подібності на множині трикутників, відношення рівносильності на множині рівнянь є симетричними.

Бінарне відношення  на множині АА називається транзитивним, якщо a, b, c : (ab  bc)  ac. Транзитивними є відношення паралельності на множині прямих, відношення подібності на множині трикутників, відношення подільності на множині натуральних чисел.

Відношення  на множині А називається відношенням еквівалентності, якщо воно водночас має властивості рефлексивності, симетричності, транзитивності.

Якщо на множині А зафіксоване певне відношення еквівалентності , то про елементи х і у, які перебувають у цьому відношенні кажуть, що вони еквівалентні. Із поняттям еквівалентності на множині А тісно пов’язане поняття класифікації елементів цієї множини або розбиття множини на класи. Кажуть, що множину А розбито на класи L₁, L₂,… L_n, якщо:

1) L₁ L₂… L_n=A;

2) L_i  L_j =, якщо i  j;

3) L_i  для всіх i =1, 2, ..., n.

Кожний клас складається з усіх еквівалентних між собою елементів. Тому ці класи називаються класами еквівалентності. Множина всіх класів еквівалентності називається фактор-множиною множини А за еквівалентністю .

Приклад 1.4. Нехай дано множину А={1, 2, 3, 4, 5}. Знайдемо будь-яке розбиття А. Виділимо з А дві підмножини: парних і непарних чисел. Отримаємо А₁={2, 4} і А₂={1, 3, 5}. Система { А₁, А₂} є розбиттям А на класи, оскільки:

1) А₁А₂=А;

2) А₁А₂=;

3) А₁, А₂.

Звичайно, множина А має і інші розбиття, наприклад { А₁, А₂, А₃, А₄, А₅}, де А₁={1}, А₂={2}, А₃={3}, А₄={4}, А₅={5}.

Приклад 1.5. Розглянемо відношення нa  : означає, що ділиться на m. Його прийнято записувати так: ( ) і читати: “ х конгруентне y за модулем m”. Так як то воно рефлексивне; так як з випливає то воно симетричне;

з того, що і випливає тому це відношення транзитивне. Отже, - відношення еквівалентності. Його класи еквівалентності – це m арифметичних прогресій …, при .

Кожен такий клас (прогресію), що відповідає значенню , далі позначаємо через . Отже , … . Елементи цієї фактор множини називають класами лишків за модулем m.

Поняття відображення (функції), як і поняття множини, є фундаментальним.

Відображенням (функцією) f з множини А в множину В ( ) називається закон, згідно якого елементам з першої множини А ставляться у відповідність елементи з другої множини В. Щоб задати конкретну функцію, потрібно задати множини А і В, та закон, який встановлює відповідність між елементами цих множин. Законом може бути або перечислення, або деяке загальне правило.

Теорема. Кожна функція визначає бінарне відношення на множині АВ, і, навпаки, кожне бінарне відношення на множині АВ визначає функцію .

Доведення. Нехай задана функція . Тобто задані множини А і В та закон f. Розглянемо прямий добуток АВ. Задамо на ньому бінарне відношення наступним чином: ab, якщо а відображається в b.

Закон відповідності між елементами xA і yB записують у вигляді y=f(x), при цьому елемент y називають образом елемента x, a x – прообразом елемента y.

Множину тих елементів xA, кожний з яких має образ, називають областю визначення відображення f і позначають D(f).

Множину тих елементів yB, для кожного з яких існує прообраз, називають множиною значень відображення f і позначають E(f).

Графіком функції f з областю визначення А і множиною значень В називають підмножину Г декартового добутку АВ, яка складається з усіх елементів (x, f(x)), де xA, f(x)B.

Функція називається ін’єктивною, якщо кожен елемент з В відповідає єдиному елементу з А. Функція сюр’єктивна, якщо для кожного елемента з В існує прообраз з А. Функція бієктивна ( взаємно однозначна), якщо вона ін’єктивна і сюр’єктивна одночасно. Якщо існує хоча б одна взаємно однозначна відповідність між множинами А і В, то вони називаються еквівалентними.

Якщо функція f є взаємно однозначною відповідністю між множинами А і В, то визначена і функція f^-1, яка буде взаємно однозначною відповідністю між множинами В і А, причому f^-1(b)=a тоді і тільки тоді, коли f(a)=b. Функцію f^-1 називають оберненою до функції f.

Суперпозицією двох даних функцій i називається функція , закон якої g_f задається наступним чином:  bB: (  ). Функція , отримана таким чином з функцій g і f називається їх композицією.

Нехай А- деяка скінченна множина, яка складається з n різних елементів : A={a₁, a₂, a₃, …, a_n}. Всі можливі скінченні впорядковані множини з n елементів, які можна отримати міняючи місцями елементи множини А називаються перестановками з n елементів.

Наприклад, (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) та (3, 2, 1) всі можливі перестановки множини {1, 2, 3}.

Кількість перестановок з n елементів дорівнює n!. Вважаємо, що порожню множину можна впорядкувати єдиним способом, тому вважається, що 0!=1.

Якщо в заданій перестановці поміняти місцями будь-які два елементи, а решту елементів залишити на своїх місцях, то отримаємо нову перестановку. Таке перетворення перестановки називається транспозицією. Наприклад, перестановка (1, 3, 2) отримується з перестановки (1, 2, 3) внаслідок обміну місцями 2 і 3.

Всі n! перестановок з n елементів можна розташувати в такому порядку, що кожна наступна перестановка буде отримуватись із попередньої однією транспозицією, причому у якості вихідної перестановки можна вибрати будь-яку з перестановок. Зокрема від довільної перестановки з n елементів можна перейти до довільної іншої перестановки з тих само елементів за допомогою декількох транспозицій. Перестановка називається парною, якщо вона отримується з перестановки з допомогою парної кількості транспозицій і непарною у протилежному випадку.

Приклад 1.6. Нехай А = ( 1; 2; 3; 4). Перестановка ( 1; 2; 3; 4) за означенням парна. Парною буде і перестановка ( 4; 2; 1; 3) так, як вона може бути отримана з перестановки (1; 2; 3; 4) за допомогою парної кількості транспозицій: поміняємо місцями в перестановці ( 4; 2; 1; 3) перший і четвертий елементи, отримаємо перестановку ( 3; 2; 1; 4) і тепер у ній міняємо місцями перший і третій елементи. Отримали вихідну перестановку ( 1; 2; 3; 4), як результат двох транспозицій. Аналогічно можна переконатися, що перестановка ( 4; 1; 2; 3) буде непарною, - вона переходить у перестановку (1; 2; 3; 4) після трьох транспозицій: ( 4; 1; 2; 3) ( 1; 4; 2; 3)  ( 1; 2; 4; 3)  ( 1; 2; 3; 4). Кожна транспозиція міняє парність перестановки, кількість парних перестановок з n – елементів дорівнює кількості непарних, тобто дорівнює n!/2.

Нехай А - деяка скінченна множина, яка складається з n різних елементів. Для простоти будемо вважати, що це перші n натуральних чисел: A={1, 2, 3, …, n}. Взаємно однозначне відображення f множини А на себе називається підстановкою n – го степеня. Для позначення підстановки f використовують запис , де (i₁, i₂, i₃, ... , i_n) та (k₁, k₂, k₃, ... , k_n) – дві перестановки з n елементів множини А (k₁, k₂, k₃, ... , k_n образи елементів i₁, i₂, i₃, ... , i_n при відображенні f). Одна і та ж підстановка n-го степеня може бути записана багатьма способами, зокрема у вигляді . При такому записі різні підстановки відрізняються перестановками, що стоять у нижній стрічці, а тому кількість підстановок n-го степеня дорівнює кількості перестановок з n елементів, тобто n!. Тотожною підстановкою називається підстановка . Якщо парності верхньої та нижньої перестановок у підстановці співпадають, то підстановка називається парною, якщо не співпадають – непарною.

Введемо операцію множення на множині підстановок n-го степеня. За означенням підстановок n-го степеня – це взаємно однозначне відображення f скінченої множини з n елементів у себе. Послідовне виконання двох підстановок n-го степеня знову буде взаємно однозначним відображенням множини А в себе і приводить до третьої підстановки n-го степеня, яку називають добутком першої з даних підстановок на другу.

Приклад 1.7. Нехай дано дві підстановки четвертого степеня і . При підстановці f число 1 переходить в 4, а при підстановці g число чотири переходить в число 2, тобто після послідовного виконання цих двох підстановок 1 перейде в 2. Аналогічно 234, 321, 413. У результаті отримуємо підстановку .

Оберненою підстановкою до підстановки n-го степеня f називається така підстановка n-го степеня g, що добуток цих двох підстановок дає тотожню підстановку : fg = gf = e.

Приклад 1.8. Знайти обернену підстановку до підстановки .

Якщо , то . Перевіримо