3.Кинематика твердого тела

Используя полученные сведения из кинематики точки, перейдём к изучению твердого тела. Абсолютно твердым телом называют такое материальное тело, расстояние между двумя любыми точками которого остаётся неизменным.

Вначале рассмотрим простейшие случаи движения тела: поступательное движение и вращение вокруг неподвижной оси. Эти движения твёрдого тела, помимо непосредственного практического значения, будут рассматриваться как составляющие в случае сложного движения.

3.1. Поступательное движение твердого тела

Поступательным называется такое движение твёрдого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе.

Примерами этого движения могут быть: движение кузова автомобиля на прямом горизонтальном участке дороги, движение корпуса угольного комбайна вдоль лавы с учетом гипсометрии пласта, движение ползуна кривошипно-шатунного механизма и т. д. Поступательное движение твердого тела может быть прямолинейным и криволинейным.

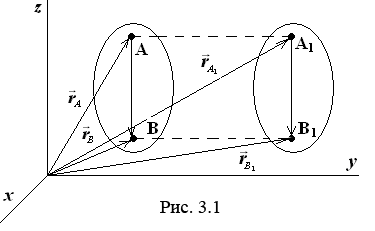
В основу теории поступательного движения положена следующая теорема: точки тела, движущегося поступательно, описывают одинаковые траектории (при наложении совпадающие) и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

= const, по модулю и направлению (твердое тело, поступательное движение).

= + (3.1)

= + (3.2)

, поэтому при наложении траектория АА совпадает с ВВ .

Возьмём производные = . Здесь , , .

Следовательно,

= = (3.3)

Взяв производную от (3.3), получим

(3.4)

3.2 Вращательное движение твердого тела

Вращательным движением твердого тела называется такое движение, при котором точки тела движутся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения тела, и описывают окружности, центры которых лежат на этой оси.

Расстояние от любой точки тела до оси называется радиусом точки.

3.2.1 Уравнение вращательного движения, угловая скорость и угловое ускорение

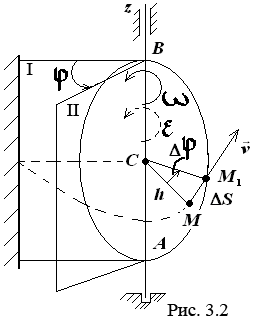
Положение тела в любое время определяется углом “ ” , изменяющимся с течением времени . Следовательно, закон вращательного движения тела

= f (t) (3.5)

Угол поворота измеряется в радианах. Он будет положительным, если поворот тела против хода часовой стрелки наблюдается с положительного конца оси АZ, если наоборот - угол отрицательный.

Средней угловой скоростью для промежутка времени t будет отношение приращения угла поворота к этому промежутку времени, т. е. . Тогда мгновенное значение угловой скорости определяется . Значит

(3.6)

Если угловая скорость задается через частоту вращения тела «n» (об/мин), тогда она определяется

(3.7)

Угловое ускорение характеризует изменение угловой скорости тела с течением времени. Поэтому . Следовательно, угловое ускорение тела в данный момент времени «t» определяется . Значит, (3.8)

Угловая скорость и угловое ускорение являются основными кинематическими характеристиками вращательного движения твердого тела. Эти величины можно изобразить в виде векторов, направленных вдоль оси вращения тела (см. рис.3.3)

П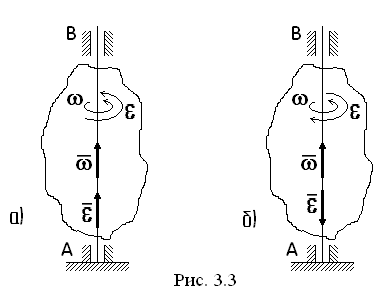 ри ускоренном вращательном движении тела направления стрелок (вдоль оси вращения) векторов и совпадают (а). В случае разного (б) направления стрелок векторов и , вращательное движение тела замедленное.