2.7 Контрольные задачи по разделу “Кинематика точки” (Задача к 1)

Точка движется в плоскости “ ”. Закон движения точки задан уравнениями , , где и заданы в метрах, - в секундах. Найти уравнение траектории точки и её положение в заданный момент времени . Определить скорость и ускорение точки, а также касательное и нормальное ускорения, радиус кривизны траектории и вычислить их значение в момент времени с.

Зависимости и приведены в таблице 2.1. Указания: задача К-1 относится к кинематике точки и может быть решена с помощью формул для определения скорости и ускорения точки при координатном способе задания движения, а также формул для определения формул касательного и нормального ускорений. В некоторых задачах при определении траектории следует учесть формулы тригонометрии

Пример решения задачи к 1.

Точка движется согласно уравнений ; ;

( , - в метрах, - в секундах).

Определить уравнение траектории точки, для момента времени с, найти положение точки, а также скорость, полное, касательное, нормальное ускорения точки и радиус кривизны траектории.

Порядок выполнения задания

1. Найдем уравнение траектории точки. Для определения уравнения траектории исключим из уравнений движения время . Из первого уравнения движения точки найдем

Из второго уравнения движения найдем

Возведя полученные значения ( правую и левую стороны уравнения ) в квадрат и складывая их находим:

1= +

Следовательно, траекторией точки является эллипс с центром в точке с координатами (3;1).

Вид траектории показан на рисунке 2.4.

Таблица 2.1

Номер варианта	Уравнения движения		t, с
	, м	, м
1	2	3	4
1	-2	t	2
2	3sin( t)-2	5cos( t)	1
3	8sin ( t)-1	4cos t+4	0
4	4cos ( t)-2	sin( t)	1
5	5sin( t)+1	5cos( )-1	2
6	t	6sin( t)	2
7	t	2t -3	1
8	4cos( t)	6sin( t)+3	2
9	3cos ( t)-3	6sin ( t)+1	1
10	Sin( t)	3cos( t)-3	1
11	6sin( t)-1	6cos( t)+2	2
12	3cos( t)	t	2
13	4t +1	2t	2
14	5sin( t)+1	3cos( t)	1
15	5sin ( t)-3	4cos ( t)+1	2
16	6cos( t)+2	sin( t)	1
17	6sin( t)+2	6cos( t)-1	2
18	2t	4sin( t)	1
19	2t	4t -1	2
1	2	3	4
20	6cos( t)+2	3sin( t)+1	1
21	cos ( t)+4	4sin ( t)+3	2
22	sin( t)	2cos( t)+4	0
23	4sin( t)+1	4cos( t)	1
24	6cos( t)	2t	1
25	9t -1	3t	1
26	6sin( t)-1	2cos( t)+2	2
27	6sin ( t)-5	2cos ( t)+3	1
28	6cos( t)-2	sin( t)	0
29	6cos( t)-2	6sin( t)-2	1
30	2t	2sin( t)	1

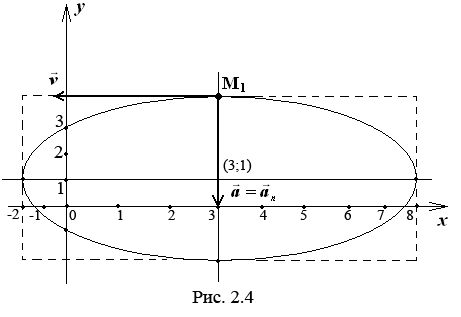
2. Найдем положение точки в момент времени t=1с

x(1) =5cos +3 = 3м; y (1) = 2 sin +1 = 3м.

Положение точки М показано на рис 2.4.

3. Найдем скорость точки М

= ,

Где = = = - sin( t), или в момент времени t =1c

(1)= - sin = -7.85(м/c)

= = = cos( t), если в момент времени t =1c , (1)= cos =0

Следовательно

4. Найдём ускорение точки.

,

где , или ,

, или

Следовательно

5. Найдем касательное ускорение точки ,

6. Найдём нормальное ускорение точки

= =

(1)= * = = 4.93 м/с

7. Найдем радиус кривизны траектории точки М,

,

=

Направление векторов показано на рис. 2.4.

Ответ:

(1)=7.85м/c; (1)= 4.93 м/c ; (1)=0 ; (1)= 4.93м/c ; м