5.3. Сложение поступательного и вращательного движений

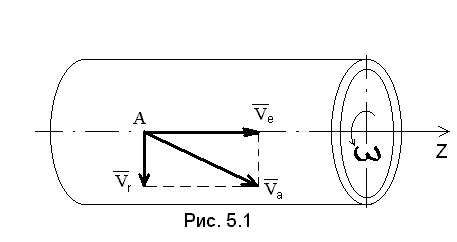
Этот вид движений можно рассмотреть на примере перемещения трубы радиусом R в процессе ее термической обработки, во время которой все точки трубы участвуют в поступательном движении вдоль оси Z и вращательном движении вокруг оси Z (см. рис. 5.1).

Точка А трубы имеет переносную скорость (поступательное движение) и относительную скорость (вращательное движение). Известно, что линейная скорость при вращательном движении определяется , т.е. . Здесь - угловая скорость при вращательном (относительном) движении точек трубы. Следовательно, абсолютная скорость точки А трубы равна . Значит

(5.2)

5.3. Сложение вращений вокруг двух параллельных осей

Рассмотрим случай, когда относительное движение тела «К» является вращение его с угловой скоростью вокруг оси «аа₁», укрепленной на кривошипе «ba» (см. рис. 5.2а), а переносное – вращением кривошипа «ba» вокруг оси «bb₁», параллельной оси «аа₁» с угловой скоростью . Следовательно, движение тела «К» будет плоскопараллельным, с учетом указанных движений и положения плоскости тела «К» (она перпендикулярна названным выше осям). При определении возможны частные случаи.

5 .3.1. Вращения направлены в одну сторону

Из рис. 5.2б легко видеть, что точка А, лежащая на оси «аа₁», получает скорость только от вращения вокруг оси «bb₁», значит . По аналогии . При этом (они оба перпендикулярны АВ) и направлены в разные стороны. Тогда точка «С» будет МЦС – мгновенным центром скоростей (см. раздел 6 «Плоскопараллельное движение твердого тела»), т.е. и ось «Сс₁» является мгновенной осью вращения. Для определения угловой скорости абсолютного вращения тела вокруг оси «Сс₁»

и положения этой оси воспользуемся равенством (из раздела о МЦС) и , или . Из свойств пропорции получим

(5.3)

Подставляя в (5.3) значение и , получим , или

(5.4)

С течением времени мгновенная ось «Сс₁» меняет свое положение, описывая цилиндрическую поверхность.

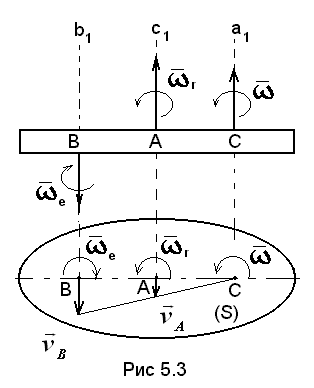
5.3.2 Вращения направлены в разные стороны

Изобразим сечение (S) тела «К» (см. рис. 5.3) и допустим, для определенности, что > . Тогда, рассуждая, как и в предыдущем случае, найдем скорости точек А и В, численно равные и ; при этом || и направлены в одну сторону. Тогда мгновенная ось вращения проходит через точку «С», причем , или по свойствам пропорций

(5.5)

Подставляя в эти равенства значения и найдем окончательно

(5.6)

а так же

(5.7)

Полученные результаты показывают, что векторы угловых скоростей при вращении вокруг параллельных осей складываются также, как и векторы параллельных сил.

5 .4. Сложение вращательных движений вокруг пересекающихся осей

Указанный вид движения можно рассмотреть на примере мельничных бегунов для растирания кусковых материалов (см. рис. 5.4) .

Угловая скорость вращения бегунов относительно геометрической оси ОА будет . Угловая скорость вращения ОВ является переносной угловой скоростью . Тогда абсолютная угловая скорость определяется , по модулю

(5.8)