2. Сводка основных уравнений теории упругости
Будем
считать, что тело занимает объем
,
а его граница
представляет
собой объединение двух поверхностей
,
где
—
часть границы тела, на которой ставятся
статические граничные условия, а
— та часть границы тела, на которой
наложены геометрические связи на тело.
Процесс деформирования описывается двумя группами величин: геометрическими (перемещения, деформации) и статическими (внешние силы, напряжения). Искомыми среди них являются напряжения, деформации и смещения, исключая, конечно, смещения точек, принадлежащих части границы тела , где они заданы по условию. На границе тела действуют два вида сил: на — заданные поверхностные силы; на — искомые реактивные поверхностные силы, обусловленные наложенными здесь на тело геометрическими связями.
При изучении геометрической, статической и физической сторон процесса деформирования упругого тела были получены (выписываются типичные представители уравнений):
1) геометрические уравнения: соотношения Коши
|
(2.1) |
и условия сплошности
|
(2.2) |
2) статические уравнения: уравнения локального равновесия
|
(2.3) |
и статические граничные условия
|
(2.4) |
на части поверхности тела.
3) физические уравнения: обобщенный закон Гука в прямой форме
|
(2.5) |
и обратной форме
|
(2.6) |
Геометрические граничные условия
|
(2.7) |
3. Принцип Лагранжа
Принцип Лагранжа известен также под названием начала варьирования деформированного состояния. О нем иногда говорят и как об энергетической трактовке метода перемещений.
3.1. Кинематически возможное варьирование. Возможные перемещения и деформации. Примем смещения за основные неизвестные и назовем кинематическим варьированием такой процесс изменения смещений, при котором остаются неизменными внешние нагрузки. Если к тому же сохраняют силу геометрические граничные условия (2.7), то такое варьирование смещений будем называть кинематически возможным.
Смещения, согласные с геометрическими связями (2.7), наложенными на тело, назовем возможными в отличии от истинных (или действительных) смещений, фактически реализуемых в теле за счет действия заданных внешних сил. Ясно, что истинные смещения удовлетворяют всем исходным данным и соотношениям теории упругости. Что касается возможных смещений, то от них требуется лишь согласие с геометрическими граничными условиями. Поэтому можно говорить о множестве возможных перемещений, всегда содержащем единственные истинные смещения.
Пусть
—
истинные смещения, а
— близкие к ним возможные смещения.
Очевидно, что
|
(3.1) |
Смещениям отвечают истинные деформации
а смещениям — возможные деформации
Беря их разность, с учетом коммутативности операций варьирования и дифференцирования по пространственным координатам находим
|
(3.2) |
Как видим, величины (3.2) вычисляются через вариации смещений по тем же соотношениям Коши, и поэтому их естественно назвать кинематически возможными вариациями деформаций.
3.2.
Принцип Лагранжа.
Хорошо известно, что тела, деформируемые
обратимым образом, способны аккумулировать
в себе потенциальную энергию
,
которая, если теперь воспользоваться
терминологией вариационного исчисления,
является функционалом, определенным
на множестве функций-смещений, т.е.
|
(3.3) |
Здесь интегрирование распространяется на весь объем тела, а подынтегральная функция
|
(3.4) |
— удельная
потенциальная энергия, являющаяся, как
известно, однозначной функцией своих
аргументов (
).
Внешние силы, действующие на упругое тело, совершают работу
являющуюся линейным функционалом перемещений.
Назовем полной энергией тела функционал
Принцип Лагранжа гласит:
Из всех возможных перемещений только истинные смещения
доставляют полной энергии линейно упругого тела минимальное значение
Аналитически это утверждение выражается следующим образом
|
(3.5) |
|
(3.6) |
В случае линейно
упругого тела
представляет собой положительно
определенную квадратичную форму
деформаций:
Именно поэтому и
в силу линейности работы
внешних сил
.
Таким образом, достаточное условие минимума полной энергии (3.6) предопределено линейной упругостью материала и для линейно упругих тел выполняется всегда. Можно показать, что сказанное справедливо и для нелинейно упругих тел и выражает способность упругих тел при деформировании аккумулировать энергию.
Значение принципа Лагранжа состоит в том, что он позволяет для достаточно широкого класса физических тел (имеются в виду упругие, обратимо деформируемые тела) получить разрешающие уравнения метода перемещений и сопутствующие им статические граничные условия. Для этого достаточно записать функционал полной энергии тела, а затем, воспользовавшись правилами вариационного исчисления, найти и приравнять нулю его первую вариацию. Вытекающие отсюда уравнения типа Эйлера дадут разрешающие уравнения, а естественные граничные условия - статические граничные условия.
Покажем, что из принципа Лагранжа вытекают статические соотношенния теории упругости. Для этого воспользуемся правилами вариационного исчисления и распишем необходимое условие экстремума полной энергии тела.
По определению полного приращения функционала
Подставляя сюда очевидное разложение в ряд Тейлора с точностью до линейных членов относительно вариаций деформаций
где были учтены формулы Грина
,
приходим к условию стационарности
,
называемому основным вариационным уравнением Лагранжа.
Принимая во внимание тождества
после преобразований с помощью формулы Остроградского-Гаусса
(
— направляющие косинусы внешней
единичной нормали поверхности
)
приходим к равенству
из которого вытекают статические соотношения (2.3), (2.4).
Таким образом, принцип Лагранжа эквивалентен статическим уравнениям теории упругости и может использоваться вместо них.
3.3. Применение принципа Лагранжа к теории изгиба балок. В этом пункте мы воспользуемся принципом Лагранжа с целью вывода дифференциального уравнения упругой линии балки и балочных статических граничных условий. Напомним с этой целью известные положения из теории изгиба балок.
Пусть балка длиной
l
находится
в состоянии равновесия под действием
распределенной поперечной нагрузки
и сосредоточенных поперечных сил
,
и моментов
,
,
приложенных соответственно на левом
(
)
и правом (
)
концах балки;
— координата
вдоль оси балки (см. рис.
3.1).
О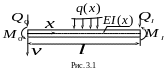
бозначим
через
— жесткость
балки на изгиб, зависящую, вообще говоря,
от
,
а через
,
и
— соответственно прогиб балки,
перерезывающую силу и изгибающий момент.
Три последние величины связаны между
собой известными соотношениями
|
(3.7) |
Уравнение упругой линии балки имеет вид
(3.8)
а балочные статические граничные условия – вид
|
(3.9) |
или в смещениях
|
(3.10) |
Выведем уравнение (3.8) и соотношения (3.10) из принципа Лагранжа.
Функционал полной энергии балки имеет вид
Для потенциальной энергии изгиба балки имеет место выражение
,
а для работы внешних сил — формула
.
Поэтому
Полученное выражение полной энергии балки напоминает функционал (1.21). Поэтому согласно (1.23)
Приравнивая это выражение нулю, найдем
Замечая, далее, что
имеем
что в точности совпадает с (3.8) и (3.10).
В заключении заметим, что все выводы настоящего пункта и другие результаты, подобные им, справедливы при более слабом требовании — выполнении принципа стационарности полной энергии тела. Это требование составляет лишь необходимую часть утверждения принципа Лагранжа.