Строительная механика

Строительная механика — прикладной раздел механики твердого тела. В нем строится модель деформирования реальной конструкции, и излагаются методы расчета таких конструкций.

Основная задача строительной механики — определение внутренних сил (напряжений) а также перемещений и деформаций в модели нагруженной конструкции.

1. Прикладная теория упругости.

Теория упругости занимается изучением процесса деформирования упругих тел. Основная задача теории упругости — определение напряженно-деформированного состояния (НДС) нагруженного или нагретого тела.

Всюду в этом курсе будем изучать статический процесс деформирования, то есть будем считать, что отсутствует временной фактор.

1. 1. Основные гипотезы теории упругости.

1. Гипотеза сплошности (континуума).

До деформации и после нее геометрический объем тела совпадает с материальным. Эта гипотеза позволяет широко использовать математический аппарат дифференциального и интегрального исчисления.

2. Гипотеза о малости перемещений и их градиентов.

Перемещения малы по сравнению с размерами тела, а градиенты (они безразмерные) намного меньше единицы. Мы ограничимся изучением геометрически линейных теорий, при описании которых перемещения и градиенты будут входить геометрически линейным образом. Все эти линейные зависимости пренебрегают градиентами по сравнению с единицей.

3. Физическая гипотеза (обобщенный закон Гука).

Меры внутренних сил (напряжений) связаны с мерами деформирования (деформациями) линейными зависимостями. Все теории, основанные на этой зависимости называются линейно-фиизическими.

4. Гипотеза о естественном состоянии тела.

В ненагруженном состоянии в телах отсутствуют напряжения и деформации.

Во всяком процессе деформирования можно выделить:

Геометрическую сторону. Она связана с изучением взаимного расположения точек тела при деформировании а также с изменением взаимного расположения точек. В дальнейшем увидим, что эти изменения могут быть полностью описаны деформациями.

Статическую сторону. Основными изучаемыми величинами являются внутренние силы, за которые мы будем принимать напряжения.

Физическую сторону. Здесь постулируется связь между напряжениями и деформациями.

Основная задача геометрической стороны процесса деформирования: введение понятия напряжений и деформаций как мер изменения взаимного расположения точек тела, а также в установлении взаимосвязи между деформациями и напряжениями.

Основная задача статической стороны: введение понятия мер внутренних напряжений и установлении их связей с заданными внешними силами.

1.2. Теория деформаций

Здесь изучается геометрическая сторона процесса деформирования.

Предположим, что известна система координат. Опишем положение тела до начала процесса деформирования. Будем характеризовать все точки вектором r

r = x i + у j + z k.

Предположим, что в процессе деформирования точка заняла другое положение, совершив перемещение

u (x, y, z) = u (r) = u i + v j + w k.

Будем считать, что u известно. То есть известны его компоненты u, v, w.

Берем точку А и произвольное направление t. Тогда

AB = dr, t = l i + m j + n k, |AB| = ds

d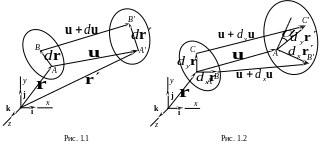 r = t /ds, |ds'| = |dr'| = |A' B'|

Определим деформацию удлинения в точке тела по некоторому фиксированному направлению t выражением

В результате преобразований получим

(1.1)

Примечание. Все формулы, выделенные красным цветом, рекомендуем знать или

понимать, как они получаются)

Предположим, что t || i. Тогда l =1, m=n=0, и — деформация удлинения вдоль оси 0x. Аналогично вдоль 0у и 0z. Они положительны, если волокна удлиняются.

Деформации описывают изменение прямого угла между соответствующими направлениям 0x, 0y, а также 0x, 0z и 0y, 0z в одной точке. Они положительны, если прямой угол уменьшается.

Величины называются декартовыми компонентами деформации. Их еще называют соотношениями Коши.

Матрица, составленная из этих компонент

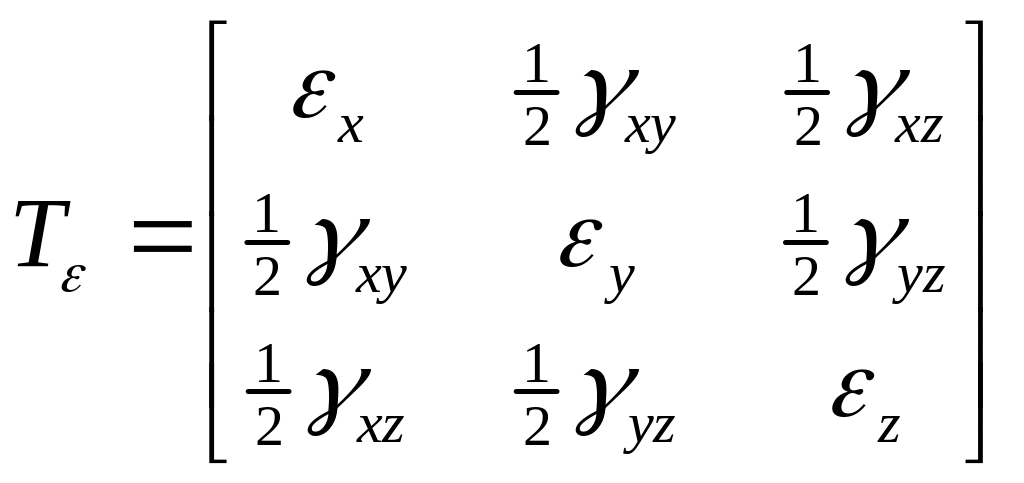
называется тензором деформаций. То есть этими выражениями определяются все декартовы линейные деформации в точке (удлинения и сдвиги).

По известным перемещениям всегда однозначно могут быть найдены деформации.