
- •080100.62 По направлению Экономика
- •Понятие функции двух независимых переменных
- •2. Производные функции двух независимых переменных
- •2.1. Частные производные первого порядка
- •2.2. Частные производные высших порядков
- •3. Полный дифференциал функции двух переменных
- •4. Касательная плоскость и нормаль к поверхности
- •5. Экстремум функции двух независимых переменных
- •5.1. Необходимое условие экстремума
- •5.2. Достаточные условия экстремума
- •6. Градиент и производная по направлению
- •7. Метод наименьших квадратов
- •8. Первообразная и неопределенный интеграл
- •Свойства интегралов
- •9. Методы интегрирования
- •9.1. Непосредственное интегрирование
- •9.2. Метод замены переменной (подстановки)
- •9.3. Метод интегрирования по частям
- •10. Интегрирование рациональных дробей
- •10.1. Простейшие дроби, их интегрирование к простейшим дробям относятся дроби вида:
- •10.2. Правильные и неправильные рациональные дроби
- •10.3. Разложение правильной дроби
- •10.4. Нахождение коэффициентов
- •10.5. Правило интегрирования рациональных дробей
- •11. Интегрирование некоторых иррациональностей
- •12. Интегрирование тригонометрических выражений
- •13. Определенный и несобственный интегралы, их вычисление
- •14. Геометрические приложения определенного интеграла
- •Из чертежа видно, что
Из чертежа видно, что

 4
x пределы
интегрирования
4
x пределы
интегрирования
будут и
 (рис.
7).
(рис.
7).
Рис.
7  .
.
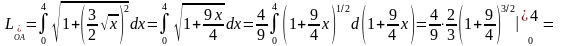

 (кв.
ед.).
(кв.
ед.).
Пример
62. Вычислить
длину одной арки циклоиды

 (рис.
8).
(рис.
8).
 Решение.
Из соотношения
видно, что значение
Решение.
Из соотношения
видно, что значение
 соответствует
соответствует
 ,
,
 соответствует
соответствует
 ,
,
 .
Так как уравнение линии
.
Так как уравнение линии
з адано
в декартовых координатах
адано
в декартовых координатах
(вид в), то используем формулу (2в),
т абл.:
абл.:
 ,
,
 .
.
t=0
t=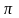 t=2
t=2
 Рис.
8
Рис.
8


 .
.
Пример
63. Вычислить
длину кардиоиды
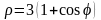 ,
,
соответствующую
 .
.
Решение. Уравнение кривой задано в полярных координатах, следовательно, при решении воспользуемся формулой (2д). Изменение задано, следовательно, выполнение чертежа необязательно.


 (ед.
длины).
(ед.
длины).
Пример
64. Вычислить
объем тела, образованного вращением
вокруг оси
 фигуры, ограниченной параболой
фигуры, ограниченной параболой
 и осью
(рис. 9).
и осью
(рис. 9).
Решение.
Парабола
расположена ветвями вниз, вершина
находится в точке
 ,
и ось
пересекает в точках
,
и ось
пересекает в точках
 .
Для решения воспользуемся формулой
(3а), табл.
.
Для решения воспользуемся формулой
(3а), табл. 

 (куб.
ед.).
(куб.
ед.).
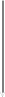 y
y


 1
1

 1
x
1
x
Рис. 9

Пример
65. Вычислить
объем тела, образованного вращением
гиперболы
 ,
отсеченной прямыми
,
отсеченной прямыми
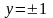 ,
вокруг оси
(рис. 10).
,
вокруг оси
(рис. 10).
Решение. Для решения задачи воспользуемся формулой (3б), табл.
y





 ;
;  ,
,
находим из уравнения гиперболы:
 -3
3
x
-3
3
x 



Рис.
10  (куб. ед.).
(куб. ед.).
Замечание: Иногда при решении задач полезно использовать рекуррентную формулу:


Знак
 (двойной факториал) означает произведение
целых чисел, начиная с
,
через одно с убыванием. Например,
(двойной факториал) означает произведение
целых чисел, начиная с
,
через одно с убыванием. Например,
 (только нечетные множители).
(только нечетные множители).
