Первая интерполяционная формула Ньютона Теоретические основы

Пусть для функции   заданы значения   для равноотстоящих значений независимой переменной:  ,  , где   - шаг интерполяции. Требуется подобрать полином   сте­пени не выше  , принимающий в точках   значения

                                                            , .                                             (1)

Условия (1) эквивалентны тому, что    при  .

Интерполяционный полином Ньютона имеет вид:

.             (2)

Легко видеть, что полином (2) полностью удовлетворяет требованиям поставленной задачи. Действительно, во-первых, степень полинома   не выше  , во-вторых,

   и     ,   .

Заметим, что при   формула (2) превращается в ряд Тейлора для функции  :

.

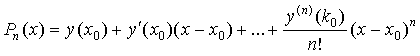    Для практического использования интерполяционную формулу Ньютона (2) обычно записывают в несколько преобразованном виде. Для этого введём новую пере­менную   по формуле     ;   тогда получим:

         ,               (3)

где   представляет собой число шагов, необходимых для достижения точки  , исходя из точки   . Это и есть окончательный видинтерполяционной формулы Ньютона.

     Формулу (3) выгодно использовать для интерполирования функции   в окрестности начального значения  , где   мало по абсолютной величине.

     Если дана неограниченная таблица значений функции  , то число   в интер­поляционной формуле (3) может быть любым. Практически в этом случае число   вы­бирают так, чтобы разность   была постоянной с заданной степенью точности. За начальное значение   можно принимать любое табличное значение аргумента  .

Блок-схема метода

Результаты решения

№1

q=(0-0)/1=0P = 1+((0 - 1 + 1)*(3)/(1) +((0 - 1 + 1)(0 - 2 + 1)*(33)/(2) +((0 - 1 + 1)(0 - 2 + 1)(0 - 3 + 1)*(-94)/(6) +((0 - 1 + 1)(0 - 2 + 1)(0 - 3 + 1)(0 - 4 + 1)*(250)/(24) Ответ:1

№2

q=(0-0)/2=0P = 0,8+((0 - 1 + 1)*(2,2)/(1) +((0 - 1 + 1)(0 - 2 + 1)*(2,8)/(2) +((0 - 1 + 1)(0 - 2 + 1)(0 - 3 + 1)*(1,2)/(6) +((0 - 1 + 1)(0 - 2 + 1)(0 - 3 + 1)(0 - 4 + 1)*(-8,88178419700125E-16)/(24) Ответ:0,8

№3

q=(0-1)/2=-0,5P = 0,5+((-0,5 - 1 + 1)*(1,5)/(1) +((-0,5 - 1 + 1)(-0,5 - 2 + 1)*(4)/(2) +((-0,5 - 1 + 1)(-0,5 - 2 + 1)(-0,5 - 3 + 1)*(3)/(6) +((-0,5 - 1 + 1)(-0,5 - 2 + 1)(-0,5 - 3 + 1)(-0,5 - 4 + 1)*(0)/(24) Ответ:0,3125

№4

q=(0-2)/2=-1P = 1+((-1 - 1 + 1)*(2,5)/(1) +((-1 - 1 + 1)(-1 - 2 + 1)*(5)/(2) +((-1 - 1 + 1)(-1 - 2 + 1)(-1 - 3 + 1)*(3)/(6) +((-1 - 1 + 1)(-1 - 2 + 1)(-1 - 3 + 1)(-1 - 4 + 1)*(0)/(24) Ответ:0,5

№5

q=(0--1)/2=0,5P = 1+((0,5 - 1 + 1)*(1)/(1) +((0,5 - 1 + 1)(0,5 - 2 + 1)*(4)/(2) +((0,5 - 1 + 1)(0,5 - 2 + 1)(0,5 - 3 + 1)*(6)/(6) +((0,5 - 1 + 1)(0,5 - 2 + 1)(0,5 - 3 + 1)(0,5 - 4 + 1)*(0)/(24) Ответ:1,375

№6

q=(0-0)/3=0P = 2+((0 - 1 + 1)*(2)/(1) +((0 - 1 + 1)(0 - 2 + 1)*(8)/(2) +((0 - 1 + 1)(0 - 2 + 1)(0 - 3 + 1)*(12)/(6) +((0 - 1 + 1)(0 - 2 + 1)(0 - 3 + 1)(0 - 4 + 1)*(0)/(24) Ответ:2

№7

q=(0--8)/1=8P = 1+((8 - 1 + 1)*(2)/(1) +((8 - 1 + 1)(8 - 2 + 1)*(2)/(2) +((8 - 1 + 1)(8 - 2 + 1)(8 - 3 + 1)*(6)/(6) +((8 - 1 + 1)(8 - 2 + 1)(8 - 3 + 1)(8 - 4 + 1)*(0)/(24) Ответ:409

№8

q=(0--6)/2=3P = 1,5+((3 - 1 + 1)*(2)/(1) +((3 - 1 + 1)(3 - 2 + 1)*(4)/(2) +((3 - 1 + 1)(3 - 2 + 1)(3 - 3 + 1)*(3)/(6) +((3 - 1 + 1)(3 - 2 + 1)(3 - 3 + 1)(3 - 4 + 1)*(0)/(24) Ответ:22,5

№9

q=(0-5)/1=-5P = 2+((-5 - 1 + 1)*(4)/(1) +((-5 - 1 + 1)(-5 - 2 + 1)*(4)/(2) +((-5 - 1 + 1)(-5 - 2 + 1)(-5 - 3 + 1)*(12)/(6) +((-5 - 1 + 1)(-5 - 2 + 1)(-5 - 3 + 1)(-5 - 4 + 1)*(0)/(24) Ответ:-378

№10

q=(0-3)/3=-1P = 2+((-1 - 1 + 1)*(-4)/(1) +((-1 - 1 + 1)(-1 - 2 + 1)*(16)/(2) +((-1 - 1 + 1)(-1 - 2 + 1)(-1 - 3 + 1)*(-18)/(6) +((-1 - 1 + 1)(-1 - 2 + 1)(-1 - 3 + 1)(-1 - 4 + 1)*(60)/(24) Ответ:100