2.4. Капиллярные явления.

Поверхность жидкости, налитой в сосуд, имеет некоторую кри­визну вблизи границы между жидкостью и твердой стенкой сосуда.

Опр. Ес­ли размеры сосуда, в котором находится жидкость, сравнимы с радиу­сом кривизны поверхности жидкости, то такие сосуды называются капиллярными. Явления, происходящие в таких сосудах, называются капиллярными явлениями.

Так как для капиллярных сосудов характерна кривизна поверх­ности жидкости в них, то здесь больше всего сказывается влияние дополнительного давления Лапласа. Непосредственным следствием этого давления является так называемый капиллярный подъём.

Θ •О Θ Θ

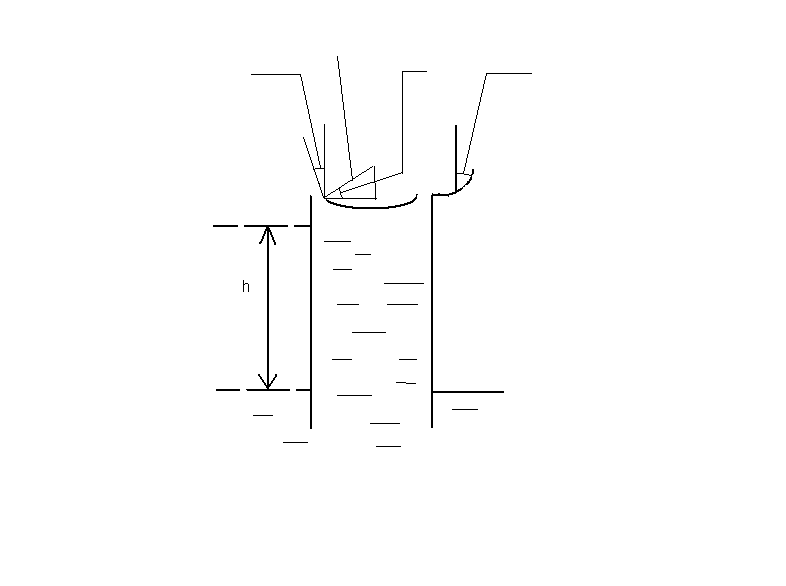
Рис. 4. Схема капиллярного подъема жидкости.

На рис. 4 изображена узкая трубка, опущенная в широкий сосуд с жидкостью. Пусть стенки трубки смачиваются жидкостью. Тогда жид­кость, проникшая в трубку, образует вогнутый мениск. Радиус трубки r сравним с радиусом мениска .

Из-за давления Лапласа жидкость, заполняющая трубку, испыты­вает давление P, направленное к центру кривизны мениска, т.е. вверх, и равное . Под действием этого давления жидкость поднимется по трубке до уровня h, при котором гидростатическое давление ρgh столба жидкости высотой h уравновешивает давление Р. То есть условие рав­новесия будет:

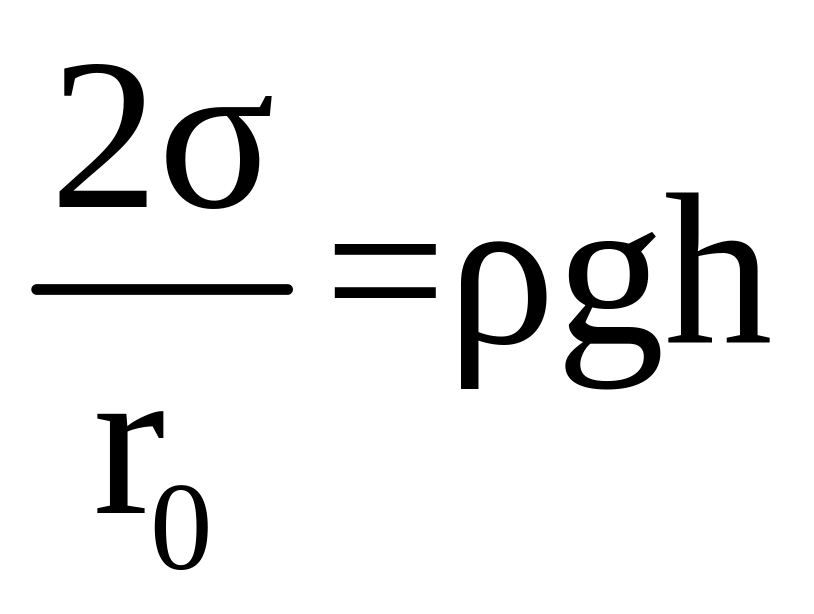(7)

где ρ - плотность жидкости.

Нетрудно установить связь между высотой подъема h и радиусом трубки r. Центр сферы, частью которой является мениск, находится в точке О (см. рис. 4). Краевой угол жидкости, соприкасающейся со стенками капилляра, равен Θ. Из рис. 4 следует, что

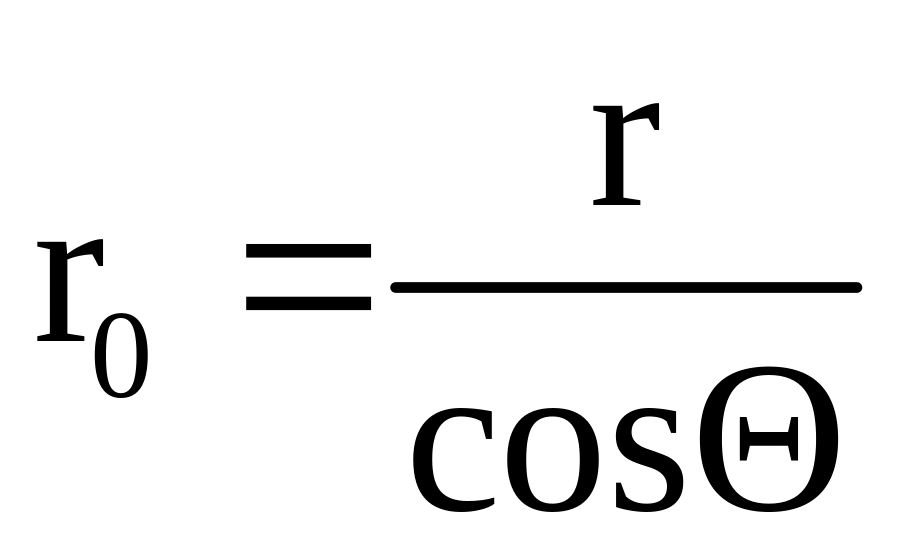
Тогда равенство (7) перепишется в виде:

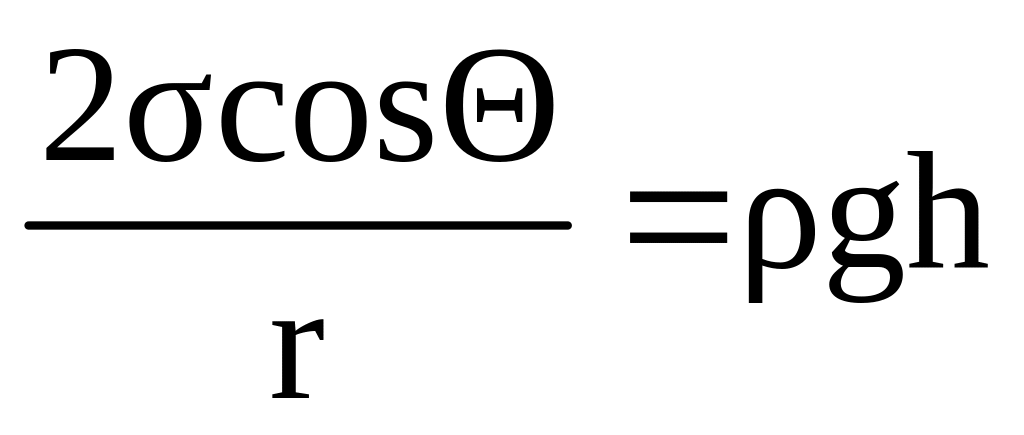
откуда

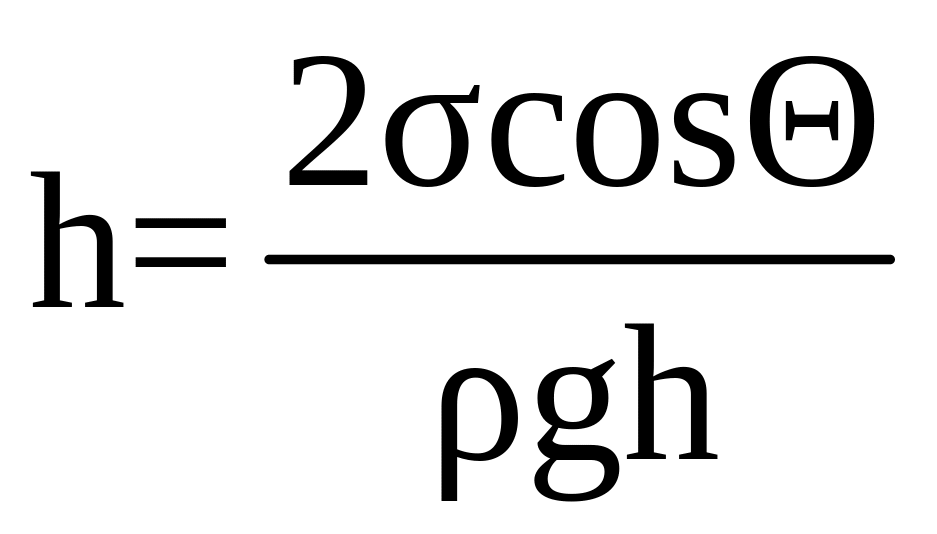(8)

В частности, дата жидкости, которая полностью смачивает стенки капилляра, то есть при Θ = 0, имеем:

h=2σ/ρgr

Итак, высота подъема жидкости в капилляре растет с уменьшени­ем радиуса капилляра и с увеличением коэффициента поверхностного натяжения.

Если жидкость не смачивает капилляра, картина будет обратной, так как мениск теперь выпуклый, центр кривизны находится внутри жидкости и давление Лапласа окажется направленным вниз. Уровень жидкости в капилляре будет теперь ниже уровня в сосуде, в который опущен капилляр (отрицательный капиллярный подъем).

3. Определение коэффициента поверхностного натяжения жидкости методом отрыва кольца.

Установка для определения величины σ (весы Жоли) изображена на рис. 5. Кольцо 1, изготовленное из материала, который хорошо смачивается исследуемой жидкостью, подвешивается на пружине дина­мометра 2. Динамометр прикрепляется к кронштейну, жестко связанно­му со штангой 5. Вдоль штанги передвигается столик 4, на котором устанавливается кювета 3 с исследуемой жидкостью. Кольцо 1 опуска­ется в жидкость. При попытке оторвать кольцо от поверхности жид­кости по внешней и внутренней окружностям кольца образуется плен­ка. Суммарная длина пленки

L = πD+π(D-2d),

где D - наружный диа­метр кольца, d - диаметр проволоки, из которой сделано кольцо. По­этому, в соответствии с (3), получим:

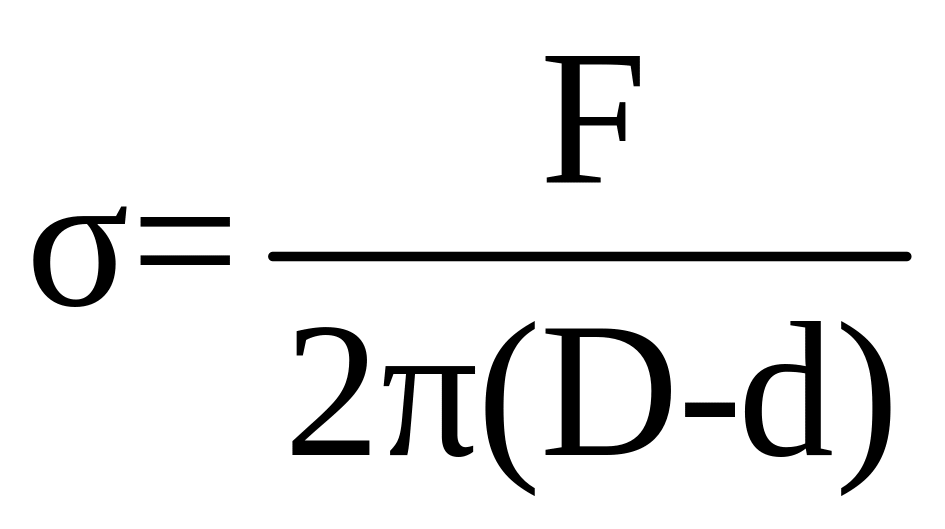, (9)

где F - сила отрыва кольца от поверхности жидкости. Эта сила измеря­ется стрелкой динамометра 2 по шкале, проградуированной в миллиньютонах (1 mН = 10^-3 Н). Перед опусканием кольца в жидкость по шкале дина­мометра измеряют силу (с точностью 0,1 mH), растягивающую пружину 2 - силу тяжести, действующую на кольцо.

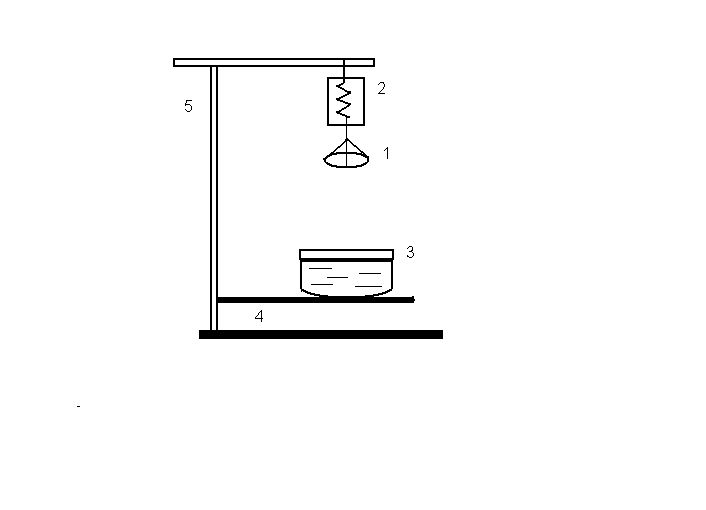
Рис. 5. Схема установки для определение коэффициента поверхностного натяжения жидкости методом отрыва кольца: 1 – металлическое кольцо, 2 - динамометр, 3 – кювета с жидкостью, 4 – передвижной столик, 5 - штанга.

Для измерения силы F кронштейн со всем устройством медленно опускают в жидкость вплоть до полного касания кольцом поверхности жидкости. Затем медленно поднимают его, растягивая тем самым пружину 2. (То же самое можно проделать, поднимая и опуская кювету с исследуемой жидкостью). В момент отрыва кольца от поверхности жидкости за­мечают показания динамометра (с той же точностью 0,1 mН). Это пока­зание, за вычетом показания динамометра перед опусканием кольца, и представляет собой искомую силу F.