
- •Розділ 7 оптимізація при нелінійній цільовій функції
- •Введення у нелінійне програмування
- •Оптимізація нелінійної функції однієї перемінної
- •Приклад 1 Приклад 3 Приклад 4 Приклад 5 Приклад 6
- •Максимізація нелінійної функції
- •Метод найшвидшого підйому
- •7.5. Квадратичне програмування
- •7.6. Сепарабельне програмування
- •7.7. Безпосередня лінеаризація
- •7.8. Максимізація опуклої цільової функції
7.7. Безпосередня лінеаризація
В
окремих випадках удається лінеаризувати
нелінійну цільову функцію
![]() ,
перетворюючи
модель в еквівалентну задачу з лінійною
цільовою функцією та лінійними
обмеженнями, а потім вирішуючи її
симплексним методом. Зрозуміло,
перетворена задача є моделлю лінійного
програмування, якщо на перемінні
накладаються лінійні обмеження. Нижче
розглядаються три важливих аспекти
безпосередньої лінеаризації.
,
перетворюючи
модель в еквівалентну задачу з лінійною
цільовою функцією та лінійними
обмеженнями, а потім вирішуючи її
симплексним методом. Зрозуміло,
перетворена задача є моделлю лінійного
програмування, якщо на перемінні
накладаються лінійні обмеження. Нижче
розглядаються три важливих аспекти
безпосередньої лінеаризації.
Мінімізація суми абсолютних значень відхилень. Розглянемо наступну нелінійну цільову функцію, що мінімізується:
![]() (7.29)
(7.29)
Для виконання необхідних перетворень доповнимо модель р лінійними обмеженнями:
![]() (7.30)
(7.30)
які можна записати в наступному вигляді:
![]() (7.31)
(7.31)
де
![]() та
та
![]() ,
, ![]() (7.32)
(7.32)
Відповідна лінійна цільова функція перетвореної моделі, що мінімізується, має вигляд
![]() (7.33)
(7.33)
Ідея
перетворення полягає в тому, що якщо
вираження в лівій частині (7.30)
позитивно,
то цьому значенню дорівнює
,
та
,
якщо негативно – цьому значенню дорівнює
(![]() ),
a
.
Оптимізація цільової функції (7.33)
забезпечує рівність нулю або
,
або
),
a
.
Оптимізація цільової функції (7.33)
забезпечує рівність нулю або
,
або
![]() ,
або і
,
і
.
Таким чином, модель лінійного програмування
складається з цільової функції (7.33),
обмежень (7.31) і (7.32), а також всіх інших
обмежень, яким повинні задовольняти
,
або і
,
і
.
Таким чином, модель лінійного програмування
складається з цільової функції (7.33),
обмежень (7.31) і (7.32), а також всіх інших
обмежень, яким повинні задовольняти
![]() (наприклад
таких, як умови незаперечності).
(наприклад
таких, як умови незаперечності).
Досягнення мінімаксу цільової функції. Тепер розглянемо наступну цільову функцію, що мінімізується:
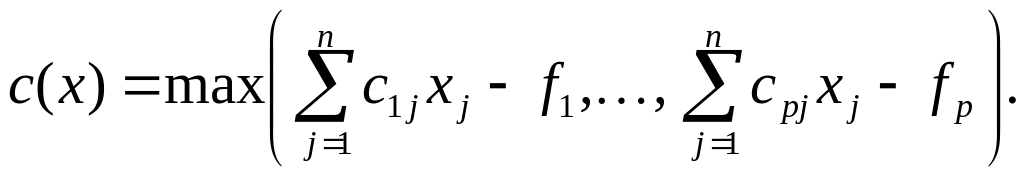 (7.34)
(7.34)
Для виконання необхідних перетворень доповнимо модель р лінійними обмеженнями
![]() (7.35)
(7.35)
які можна записати в наступному вигляді:
![]() (7.36)
(7.36)
Тут у – перемінна, на знак якої не накладається обмежень. Лінійна цільова функція перетвореної моделі має вигляд
Мінімізувати у. (7.37)
Припустимо, що в (6) представляється у такий спосіб:
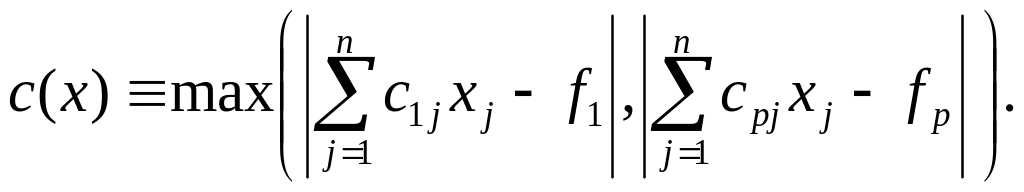 (7.38)
(7.38)
Помітимо, що
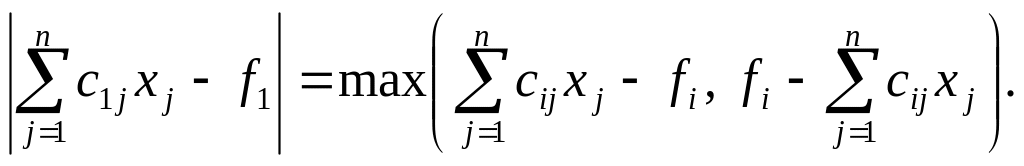
Отже, на додаток до (7.36) і (7.37) модель максимізації цільової функції (7.38) повинна включати обмеження
![]() (7.39)
(7.39)
та
![]() .
Цільову функцію (7.38) іноді називають
критерієм
Чебишева:
у
ній мінімізується найбільше абсолютне
відхилення.
.
Цільову функцію (7.38) іноді називають
критерієм
Чебишева:
у
ній мінімізується найбільше абсолютне
відхилення.
Як
(7.34) і (7.38), так і цільова функція (7.29), що
мінімізує суму абсолютних значень
відхилень, використовуються для
вирівнювання кривих і в задачах
регресійного аналізу. Обчислюється р
наборів
показників коефіцієнтів
![]() для
п
незалежних
перемінних, де р
>
п,
a
для
п
незалежних
перемінних, де р
>
п,
a
![]() – відповідні значення залежної
перемінної. Тоді
–
коефіцієнти регресії, значення яких
необхідно вибрати для вирівнювання
кривої.
– відповідні значення залежної
перемінної. Тоді
–
коефіцієнти регресії, значення яких
необхідно вибрати для вирівнювання
кривої.
Задача дрібно-лінійного програмування. Нехай функція, що мінімізується, має вигляд
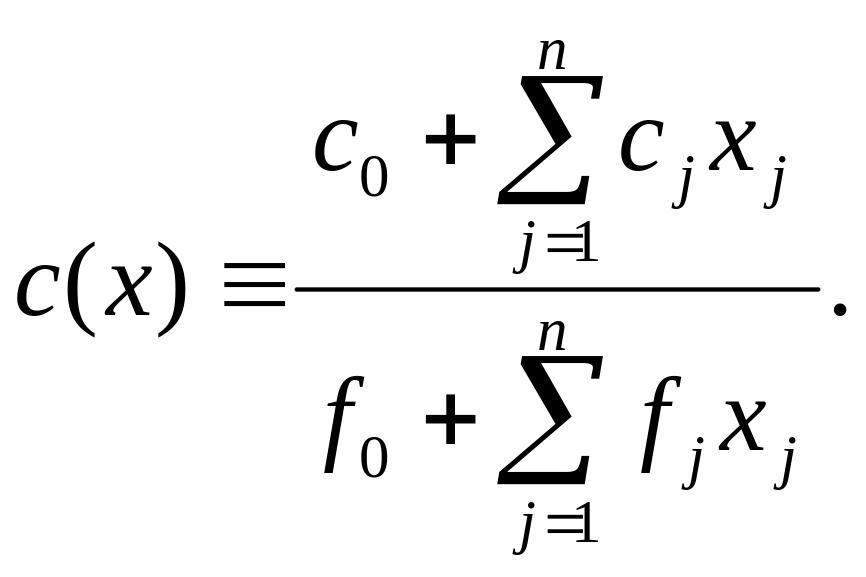 (7.40)
(7.40)
(Цю модель звичайно називають моделлю дрібно-лінійного програмування, а іноді – моделлю гіперболічного програмування).
Для того щоб при поясненнях уникнути необхідності розгляду безлічі різних можливих варіантів, припустимо, що на накладаються такі обмеження, при яких знаменник у (7.40) строго позитивний для всіх припустимих значень , а також що максимум є кінцевим.
Для того щоб перетворити задачу дрібно-лінійного програмування в модель лінійного програмування, введемо перемінну r, визначивши її в такий спосіб:
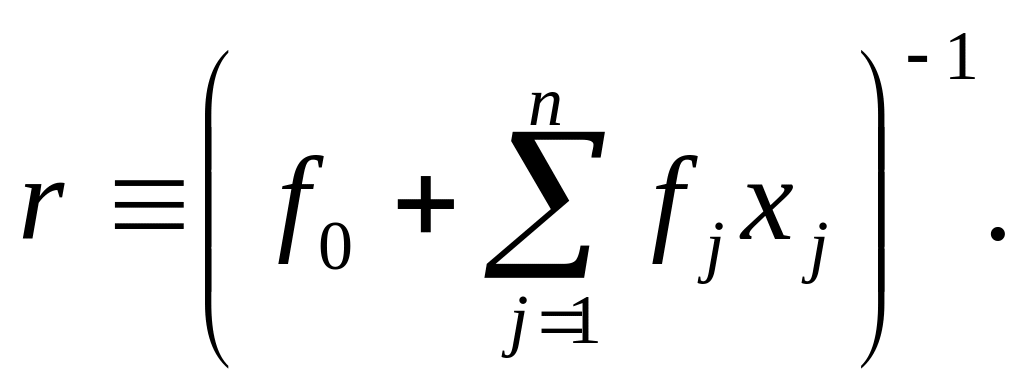 (7.41)
(7.41)
Тоді (7.40) можна записати в наступному вигляді:
![]() (7.42)
(7.42)
Відповідно до зроблених допущень, r > 0 при всіх допустимих значеннях . Зробимо заміну перемінних:
![]() (7.43)
(7.43)
Перетворена модель має вигляд
Максимізувати ![]() (7.44)
(7.44)
де відповідно до (7.41) перемінні r та у задовольняють лінійним обмеженням
![]() (7.45)
(7.45)
та r > 0. Відзначимо, що заміна перемінних на основі (7.43) повинна бути виконана також у всіх обмеженнях, що накладаються на . Так, наприклад, якщо є додаткові лінійні обмеження
![]() (7.46)
(7.46)
то перетворені обмеження можна побудувати, помноживши кожне з рівнянь (7.46) на r, що дає
![]() (7.47)
(7.47)
Модель (12) застосовується в деяких задачах планування виробництва, де виникають відходи. Так, нехай знаменник (7.40) характеризує загальна кількість використовуваної сировини, а чисельник – кількість корисна використовуваної сировини (за винятком відходів); тоді відношення, що максимізується – частка корисно використовуваної сировини.
