7.6. Сепарабельне програмування

У попередньому розділі було показано, що для рішення задач квадратичного програмування потрібно лише незначна модифікація симплексного методу. При цьому використовувалася та обставина, що часткові похідні квадратичної цільової функції лінійні. У цьому розділі переходимо до викладу іншого підходу до рішення нелінійних задач, пов’язаного з іншою модифікацією симплексного алгоритму. Метод застосуємо до задач, в яких усі нелінійні функції сепарабельні (цей термін роз’ясняються нижче). Ідея полягає у побудові задачі на умовний оптимум, що є лінійною апроксимацією вихідної задачі. При апроксимації розмір моделі зростає, однак, оскільки як метод рішення використовується варіант симплексного методу, даний алгоритм має значну практичну цінність. При даному підході однаковою мірою можлива апроксимація як нелінійної цільової функції, так і нелінійних обмежень; обидва ці випадку розглядаються нижче.

Сепарабельні цільові функції. Припустимо, що цільову функцію можна представити у виді суми п функцій, по одній для кожної з перемінних :

(7.13)

така функція називається сепарабельною. У даному контексті не будемо конкретизувати, чи необхідно максимізувати або мінімізувати функцію . Для простоти викладу метод описується тільки для однієї перемінної і відповідної функції ; зовсім аналогічні побудови застосовні для кожної з інших перемінних. Крім того, оскільки розглянуті нижче операції робляться тільки над однією перемінною , доцільно опустити підрядковий індекс і казати просто про перемінну х.

Для простоти викладу припустимо також, що, відповідно до наявних зведень, х має знаходитися на сегменті .

Для лінеаризації виберемо деяку „мережу” значень х, побудовану у такий спосіб: . Потім будь-яке значення х будемо виражати у вигляді середньозваженої :

(7.14)

де ваги w_k задовольняють умові

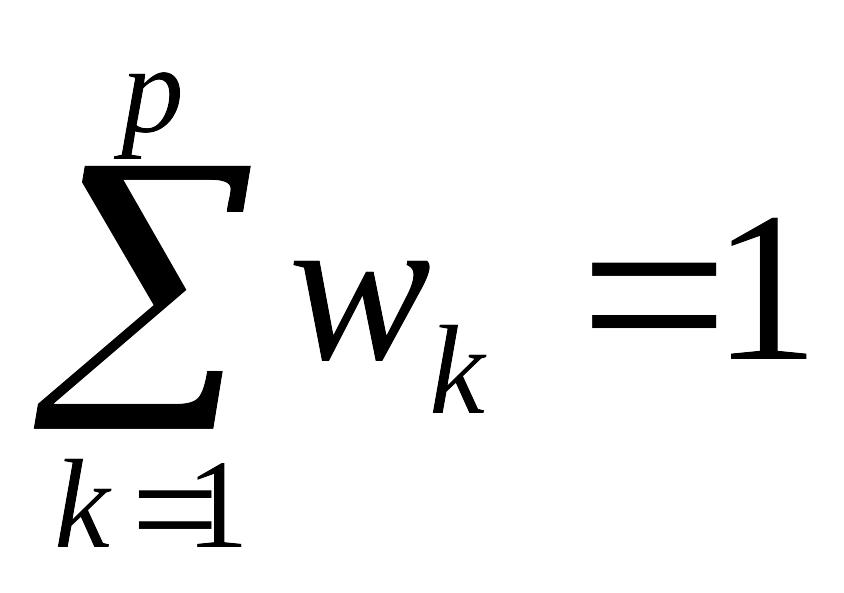та (7.15)

При побудові „мережі” завжди варто керуватися наступним зручним правилом: якщо на деякому інтервалі значень функція лінійна, те цьому інтервалу повинно відповідати не більше двох точок мережі.

Для побудови „апроксимованої” моделі замінимо х, де б ця перемінна не зустрічалася в обмеженнях, на праву частину (7.14), включимо в модель обмеження (7.15), а в цільовій функції (7.13) замінимо її кусочно-лінійною апроксимацією:

(7.16)

Для того, щоб продемонструвати відповідні побудови, розглянемо опуклу функцію та інтервал зміни, 0 < x₁ < 10 (рис. 7.4).

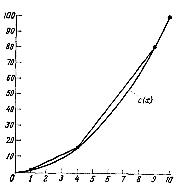
Рис. 7.4. Лінійна апроксимація функції

Нехай у даному прикладі точки мережі обрані наступними: 0, 1, 4, 9, 10. Тоді (7.14) має вигляд

(7.17)

а (7.16) представляється в такий спосіб:

(7.18)

Нехай х = 6. Тоді виразу (7.17) відповідають ваги , , інші w_k = 0. При цьому наближене значення (7/18) дорівнює , тоді як дійсне значення c₁(6) = 36.

Припустимо, далі, що на накладене обмеження

. (7.19)

Підставивши вираз для х з (7.17) у (7.19), перепишемо це обмеження у вигляді

(7.20)

При аналізі чисельного приклада передбачалося, що у випадку х = 6 варто використовувати ваги та , оскільки 6 розташовано між крапками сітки Х₃ = 4 та Х₄ = 9. Однак ваги та також дають у (7.17) значення 6, тільки у цьому випадку наближене значення c₁(6) у (7.18) дорівнює 10² ∙ 0,6 = 60. Отже, щоб (7.16) дійсно представляло б собою бажану кусочно-лінійну апроксимацію , важливо, щоб у рішенні використовувалися позитивні значення або одного, або як максимум двох ваг для суміжних точок мережі w_k та w_k+1. Можна легко сформулювати наступну властивість.

Властивість ваг суміжних точок. Якщо всі обмеження є лінійними, повинна максимізуватися, a є увігнута функція, то будь-яке оптимальне рішення апроксимуючої моделі, побудоване з використанням (7.14), (7.15) та (7.16), включає одну вагу w_k або не більш двох ваг w_k та w_k+1 з позитивними значеннями для суміжних точок. Та ж властивість рішення зберігається й у тому випадку, коли мінімізується, а опукла.

Важливим наслідком цієї властивості є наступна обставина: якщо поставлені умови задовольняються для всіх , а всі обмеження, що накладаються на лінійні, те перетворена модель являє собою задачу лінійного програмування і може бути вирішена за допомогою звичайного симплексного методу. Якщо при цьому вихідна модель включає т лінійних нерівностей, то розширена модель складається з т + п обмежень, де п додаткових обмежень мають вигляд (7.15). Отже, оптимальне базисне рішення може включати всі п перемінних з позитивними значеннями (поряд з т перемінними, що доповнюють). Крім того, рішення, що виникає, є апроксимацією глобального оптимального рішення вихідної задачі.

Однак, якщо поставлені умови не задовольняються, наприклад, якщо максимізується, a опукла, рішення апроксимованої моделі звичайно не має властивість ваг суміжних точок. Ці труднощі можна усунути, модифікувавши в деталях критерій I симплексного методу так, щоб дана властивість виконувалася в обов’язковому порядку. Це виражається у вигляді наступної конкретної умови: якщо на деякій ітерації вага w_k входить у поточний базис, то може розглядатися питання про введення в рішення тільки суміжних ваг w_k та w_k+1. Якщо ж у поточний базис входять дві суміжних ваги w_k та w_k+1 то на даній ітерації не може розглядатися питання про введення інших ваг, що відносяться до цієї ж перемінної. Ця модифікація називається правилом обмеженого введення в базис. Якщо поставлені вище умови не задовольняються й використовується правило обмеженого введення в базис, одержуване рішення є не більш ніж наближенням до локального оптимального рішення вихідної задачі.

Замість методу середньозважених, при якому в системі обмежень повинні бути додані обмеження (7.15), можна використовувати інший підхід, пов’язаний зі збільшенням числа ненегативних, обмежених зверху перемінних. Дану ідею легко усвідомити на основі приведеного вище приклада. Замість (7.14) представимо х у вигляді суми

(І)

де

У даному прикладі замість (7.17) маємо

(ІІ)

де умови незаперечності й обмеженості перемінних зверху представляються у вигляді

(ІІІ)

Тепер замість (7.16) використовується

(IV)

де

(V)

Таким чином, є тангенс кута нахилу лінійного відрізка, що апроксимує між точками та . У цьому прикладі (IV) має такий вигляд:

(VI)

При х = 6 представленню (II) відповідає наступний набір значень y_k: = 1, , та . У (VI) це дає як наближення до значення цільової функції, що дорівнює 42.

Використовувавши (II), перепишемо (7.19) у вигляді

(VII)

Якщо всі обмеження моделі лінійні, можна скористатися симплексним алгоритмом з двосторонніми обмеженнями на перемінні.

При такій постановці властивість ваг суміжних точок виражається аналогічним формулюванням: може приймати позитивні значення тільки в тому випадку, якщо значення дорівнює його верхній межі, тобто . Для того щоб зрозуміти, чому у випадку дотримання тих же умов, що і раніше, рішення при даній постановці зберігає описану властивість, розглянемо чисельний приклад.

Помітимо, що перед усіма перемінними в (VII) знаходяться однакові коефіцієнти, так що вони впливають на забезпечення обмежень. Однак опуклість обумовлює монотонне зростання коефіцієнтів у (VI). Отже, якщо завдання полягає в мінімізації , то, перш ніж у пробне рішення ввійде , перемінна повинна прийняти максимальне-можливе значення.

При подібній постановці задачі, коли всі обмеження лінійні, симплексний алгоритм з двосторонніми обмеженнями на перемінні також може бути модифікований з урахуванням правила обмеженого введення в базис, що обумовлює обов’язкове виконання властивості ваг суміжних точок. На будь-якій ітерації може бути введене в рішення тільки в тому випадку, якщо входить у базис, причому з максимально допустимим значенням, рівним ; може бути виключена з базису, тільки тоді, якщо не входить у базис і має нульове значення.

Сепарабельні обмеження. Нехай оптимізаційна задача включає сепарабельні обмеження

(7.21)

Тут можуть бути використані викладені вище методи лінеаризації. Знову розглянемо тільки одну перемінну х₁ та відповідну функцію . Нехай лінеаризація заснована на представленні (7.14) – (7.15). Вираз

(7.22)

що є кусочно-лінійною апроксимацією, підставимо в (7.21) замість а.1 .

Якщо всі обмеження сепарабельні, як (7.21), і кожна зі складових їхніх функцій опукла, то використання перетворення (7.22) приводить до оптимального рішення, що має властивість ваг суміжних точок. Таке рішення є наближенням до глобального оптимуму вихідної задачі. Якщо хоча б одна зі складових функцій не опукла, то для забезпечення цієї властивості, можливо, прийдеться додати до критерію I симплексного методу правило обмеженого введення в базис, як це було зроблено вище. У результаті можливе одержання локального, а не обов’язково глобального оптимального рішення вихідної задачі.

Досягнення сепарабельності. Підведемо підсумки. Нехай оптимізаційна задача в цілому може бути сформульована у такий спосіб:

Максимізувати

(7.23)

при умовах

(7.24)

де (7.24) може також включати обмеження незаперечності перемінних. Тоді описані вище методи дозволяють перетворити модель у таку задачу, де всі нелінійні функції апроксимуються за допомогою кусочно-лінійних функцій. Якщо усі без винятку увігнуті, а всі опуклі, то рішення, отримане за допомогою симплексного алгоритму, буде глобальним оптимумом для апроксимуючої моделі і, можна сподіватися, гарним наближенням до глобального оптимального рішення вихідної задачі. Якщо ж ці умови не задовольняються, то, модифікуючи симплексний метод, можна відшукати хоча б локальний оптимум апроксимуючої задачі.

Важливість цього підходу залежить від двох факторів. Один з них – можливість сформулювати нелінійну задачу таким чином, що цільова функція та обмеження включають тільки сепарабельні функції; цей аспект обговорюється нижче. Другий фактор – обчислювальні труднощі, що виникають при даному методі; цей аспект обговорюватиметься далі.

Дуже велике число нелінійних виражень можна привести до сепарабельному вигляду, вводячи додаткові перемінні та обмеження. До деякої міри ці методи є нестандартними – їх можна навіть скоріше назвати „спеціальними прийомами”, – і, отже, їх не можна класифікувати систематично. Однак на двох прикладах можна показати характер використовуваних підходів.

Нехай або в цільовій функції, або в обмеженнях, або в тих та інших функціях є добутки двох виразів:

. (7.25)

Простий приклад цього – добуток . По-перше, для досягнення сепарабельності замінимо усюди добуток (7.25) однієї перемінної w. По-друге, введемо ще дві перемінні у та z, зв’язавши їх двома визначальними обмеженнями:

та (7.26)

Якщо самі функції та є сепарабельними, те обмеження (7.26) сепарабельні по всіх перемінних; якщо ж ні, то необхідно застосувати додаткові перетворення для трансформації та у сепарабельні функції. По-третє, для завершення процесу накладемо сепарабельне обмеження, що зв’язує w з у та z:

(7.27)

Це забезпечує справедливість рівняння

.

Помітимо, що функція в (7.27) не є опуклою. Коротше кажучи, добуток (7.22) всюди виключається, замість нього підставляється w, а до моделі додаються обмеження (7.26) і (7.27). Можна переконатися в тому, що якщо (7.25) попросту має вигляд , то для перетворення будуть потрібні три додаткових обмеження та три додаткові перемінні.

Як другий приклад розглянемо модель, що включає вираз

(7.28)

де для всіх допустимих . Тут замість (7.28) підставимо функцію e^w, а до моделі додамо визначальне обмеження

. (7.29)

Хоча функція (7.29) сама не є сепарабельною, її можна зробити такою за допомогою того ж методу, що був використаний для досягнення сепарабельності виразу (7.25), прийнявши .