3. Максимізація нелінійної функції

багатьох перемінних без обмежень

У цьому та у наступних розділах розглядається максимізація функцій дійсних перемінних , де кожна з перемінних може приймати будь-які дійсні значення, позитивні або негативні.

Для того щоб забезпечити застосовність алгоритмів рішення, як і в попередніх розділах, нам приходиться робити відомі допущення щодо цільової функції. Виражаючись не зовсім строго, ми постулюємо, що функція є гладкою й досягає кінцевого максимуму при кінцевих значеннях . Скорочено позначаючи набір значень символом х, а вираження – символом , зроблені допущення можна записати більш строго:

I) При всіх значеннях х функція однозначна і кінцева.

II) При всіх значеннях х кожна часткова похідна однозначна, кінцева та безперервна, так що функція також безперервна.

III) Функція має кінцевий максимум .

IV) При будь-яких можливих значеннях , наприклад с, існує таке кінцеве число , що усіляка величина , якщо .

При наявності перших трьох допущень з (IV) випливає, що приймає максимальне значення с при кінцевих значеннях . Фактично ж з (IV) походить ще сильніша властивість: якщо задано будь-яке можливе значення с функції , то значення , що перевищують с, можуть відповідати лише , що знаходиться у межах кінцевих сегментів, тобто для кожного j (причому і залежить від c).

Використовуючи математичну термінологію, можна сформулювати ці чотири допущення більш коротко. По-перше, допущення II) можна переформулювати, сказавши, що функція повинна бути безупинно диференцьованою; з цього походить допущення I) і безперервність . По-друге, поставимо умову, що для будь-якого х' множини х, таких, що , є компактним (замкнутим та обмеженим); з цього випливає допущення IV).

Оскільки безперервна функція має кінцевий максимум на компактній множині, два коротко сформульованих постулати мають як наслідок допущення III).

Користуючись диференціальним вирахуванням, можна сформулювати наступне положення.

Необхідна умова існування максимуму. При допущеннях I) – III) функція має максимум у тільки в тому випадку, якщо 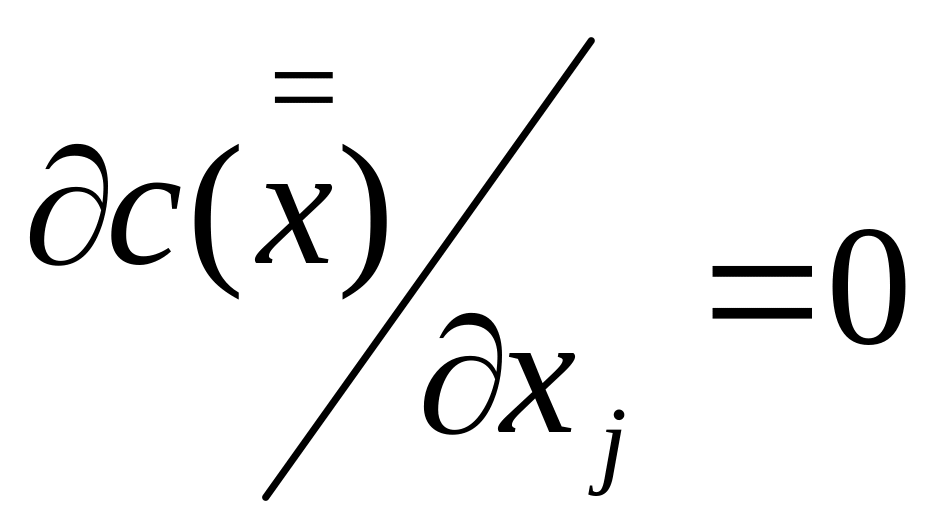для всіх j = 1, 2, … , n.

Алгоритмічний метод. Багато обчислювальних методів максимізації можна представити в стандартному вигляді.

Крок 1. Виберемо в якості вихідної довільну пробну точку х⁰.

Крок 2. Припинимо розрахунки, якщо в пробній точці x^k для j = 1, 2, … , n. У cупротивному випадку визначимо значення для j = 1, 2, … , n та перейдемо до кроку 3.

Крок 3. Визначимо нову пробну точку

для j = 1, 2, … , n. (7.8)

Повернемося до виконання кроку 2, замінивши на . Для більшості нелінійних цільових функцій ітеративний процес не дозволяє знайти таке значення , що всі . Отже, за критерієм закінчення розрахунків, зазначеному у кроці 2, виконання алгоритму ніколи не завершується; розрахунки приходиться припиняти, коли близько до оптимуму. Для того, щоб забезпечити закінченість числа ітерацій, можна, наприклад, установити граничне їхнє число або ж завершувати розрахунки, коли всі значення виявляться досить малими.

У різних алгоритмах використовуються різні методи вибору на кроці 2. Багато цих методів засновані на наступній ідеї. По-перше, вибирається так називаний напрямок для j = 1, 2, … , n; цей вибір зазвичай ґрунтується на інформації про поводження біля точки , що перевіряється, тобто на локальних властивостях . По-друге, вибирається довжина кроку t^k, заснована на інформації про поводження за межами околиці точки x^k при русі в обраному напрямку . Нарешті, напрямок і довжина кроку поєднуються у величинах . (7.9)

Якщо задані напрямки для , то проблема вибору відповідної оптимальної довжини кроку є усього лише одномірною оптимізаційною задачею:

(7.9)

Іншими словами, кожний з аргументів функції попросту має вигляд , або, у короткому записі, ; отже, функція залежить від єдиної перемінної t. Оптимальною довжиною кроку є таке значення t, що максимізує , що символічно представлено в (7.9); нова точка х — це .

Тепер можна вказати на основне розходження між лінійними та нелінійними оптимізаційними задачами. В лінійній задачі значення цільової функції змінюється на c_і при зміні x_і на одиницю поза залежністю від значення x_i та від значень всіх інших x_j. В нелінійній задачі зміна значення цільової функції при зміні x_і на одиницю може залежати від значень x_і і всіх інших x_j. Саме ця залежність є джерелом труднощів при виборі напрямку на кроці 2.